[Alg]排序算法之分布排序
作者:屎壳郎
日期:Aug 2021
版次:初版
简介: 分布排序是与归并排序截然相反的处理思路,归并排序是逐步融合归并,而分布排序是分组然后合并,再分组再合并,所以分布排序又称为“桶排序”、“基数排序”或“数排 序”。它基于键值数字特性字分类,从而避免了比较操作。
1、引言
假设要对52张扑克牌排序,定义牌面键值顺序:
A
<
2
<
3
<
4
<
5
<
6
<
7
<
8
<
9
<
10
<
J
<
Q
<
K
A<2<3<4<5<6<7<8<9<10<J<Q<K
A<2<3<4<5<6<7<8<9<10<J<Q<K
定义花色键值顺序:
?
<
?
<
?
<
?
\clubsuit<\diamondsuit<\heartsuit<\spadesuit
?<?<?<?
两张牌确定先后顺序的条件为(i)它的花色小于另一张,或者(ii)两个花色相同,但牌面值小于另一张。通常的排序方法类似于基数交换排序(见《[Alg]排序算法之交换排序》,先根据花色分成四堆,然后再根据牌面值调整每一堆中牌的顺序。
还有一种更快的方法处理这类排序!首先根据牌面值分成13堆,先对这13堆排好序,即 A < 2 < ? < K A<2<\cdots<K A<2<?<K;然后再根据花色分为4堆。然后合并到一起就得到排好序的结果。这个方法乍一看不显然。在第二步按花色分类时,如果两张牌进入不同的堆,说明花色不一样,会根据花色排序;如果两张牌具有一样的花色,那在第一步分类时已经排好序。同样的思想也可以应用到数字或字母类型的任意字典序的排序上。
设 N N N个记录,分成 M M M堆,每个堆的容量要保证能容纳 N N N个记录,这就需要 M ( N + 1 ) M(N+1) M(N+1)的空间,这就是大部分人拒绝这个算法的原因。
2、基数排序
下面介绍一种基于键值的基数,采用链表法的排序算法,姑且称之为基数排序。下面举一个以10进制为基数排序的例子。
503
??
087
??
512
??
061
??
908
??
170
??
897
??
275
??
653
??
426
??
154
??
509
??
612
??
677
??
765
??
703
503\;087\;512\;061\;908\;170\;897\;275\;653\;426\;154\;509\;612\;677\;765\;703
503087512061908170897275653426154509612677765703
第一趟遍历,以个位数为基准分堆,结果如下:
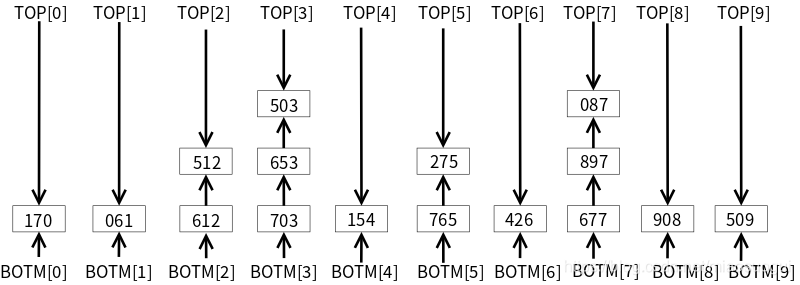
完成后重新串连起来,见图中红色线(算法H):
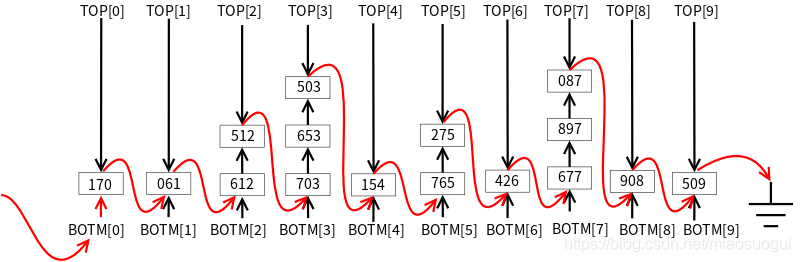
第二趟遍历,以十位数为基准分堆,结果如下:
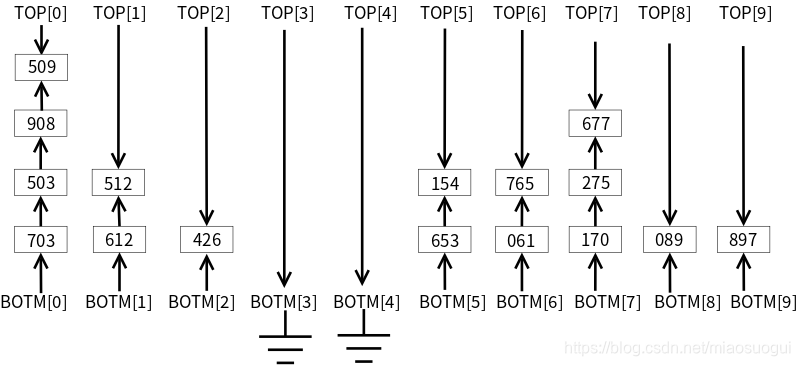
第三趟遍历,以百位数为基准分堆,结果如下:
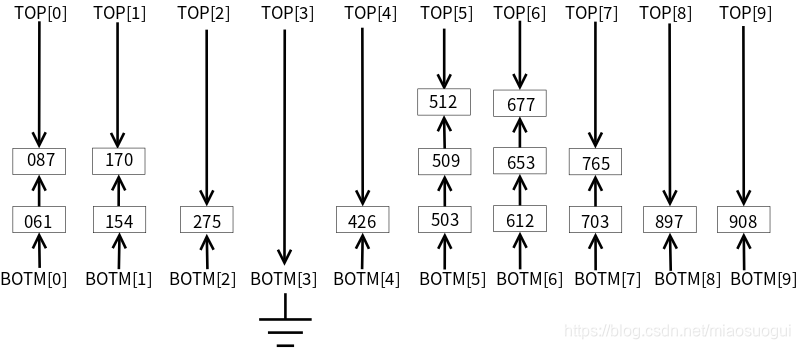
总结算法如下:
算法R:(基数排序)
设记录
R
1
,
R
2
,
…
,
R
N
R_1,R_2,\ldots,R_N
R1?,R2?,…,RN?,包含链接地址。其对应的键值为:
(
a
1
,
a
2
,
…
,
a
p
)
,
0
≤
a
i
<
M
.
(a_1,a_2,\ldots,a_p),\qquad 0\leq a_i<M.
(a1?,a2?,…,ap?),0≤ai?<M.
M
M
M为基数,其键值可表示为:
a
1
M
p
?
1
+
a
2
M
p
?
2
+
?
+
a
p
?
1
M
+
a
p
a_1M^{p-1}+a_2M^{p-2}+\cdots+a_{p-1}M+a_p
a1?Mp?1+a2?Mp?2+?+ap?1?M+ap?
- R1.[循环k] 在开始阶段,置 P ← L O C ( R N ) P\gets LOC(R_N) P←LOC(RN?),把指针指向最后一项。然后 k = 1 , 2 , … , p k=1,2,\ldots,p k=1,2,…,p,执行R2至R6,即完成一趟遍历。
- R2.[清空堆] 置 T O P [ i ] ← L O C ( B O T M [ i ] ) TOP[i]\gets LOC(BOTM[i]) TOP[i]←LOC(BOTM[i]), B O T M [ i ] ← Λ BOTM[i]\gets \Lambda BOTM[i]←Λ for 0 ≤ i < M 0\leq i<M 0≤i<M。
- R3.[解析键值 k k k位] 置 i ← a p + 1 ? k i\gets a_{p+1-k} i←ap+1?k?,即取键值 k k k有效位。
- R4.[调整链接] 置 L I N K ( T O P [ i ] ) ← P LINK(TOP[i])\gets P LINK(TOP[i])←P,然后置 T O P [ i ] ← P TOP[i]\gets P TOP[i]←P。
- R5.[移至下一个] 如果 k = 1 k=1 k=1(第一趟)并且 P = L O C ( R j ) P=LOC(R_j) P=LOC(Rj?)且 j ≠ 1 j\neq1 j?=1,置 P ← L O C ( R j ? 1 P\gets LOC(R_{j-1} P←LOC(Rj?1?并返回R3。如果 k > 1 k>1 k>1,置 P ← L I N K ( p ) P\gets LINK(p) P←LINK(p)且 P ≠ Λ P\neq\Lambda P?=Λ,返回R3。
- R6.[执行串连程序] 置 P ← B O T M [ 0 ] P\gets BOTM[0] P←BOTM[0],作为链表头,重新串连链表。
算法H:(串连链表)
- H1.[初始化] 置 i ← 0 i\gets0 i←0。
- H2.[指向堆的顶端] 置 P ← T O P [ i ] P\gets TOP[i] P←TOP[i]。
- H3.[下一堆] i ← i + 1 i\gets i+1 i←i+1。如果 i = M i=M i=M,置 L I N K ( P ) ← Λ LINK(P)\gets\Lambda LINK(P)←Λ并结束。
- H4.[是空堆吗?] 如果 B O T M [ i ] = Λ BOTM[i]=\Lambda BOTM[i]=Λ,返回H3。
- H5.[把堆链起来] 置 L I N K ( P ) ← B O T M [ i ] LINK(P)\gets BOTM[i] LINK(P)←BOTM[i]。返回H2。
在《[Alg]排序算法之计数排序》中,讲了一个非常天才的分布统计排序,可以结合上述的基数排序使用,但前提是基数排序必须从最高有效位向低有效位分类。因为分布统计排序不是一个稳定的排序算法,而基数排序后续的分类基于前面排序的结果的,分布排序的不稳定性会破坏这个前提。但从最高有效位开始,就可以消除这种隐患,从最高位开始还有另一个好处,就是我们不用完全使用基数排序,可以只派前 p p p位,剩余的可以采取其它排序算法来处理,以提高效率。
下面谈谈基数排序和基数交换排序的区别:
- 1、基数交换排序是从最高有效位开始的,基数排序是从低位向高位(当然从高为向低位也可以);
- 2、两种排序算法都不需要比较键值;
- 3、基数交换排序是分成两组,而基数排序分组是可变的(人为选定,可以2,4,8,16都行);
- 4、基数排序的运行时间是固定的 O ( N lg ? K ) O(N\lg K) O(NlgK),而基数交换排序依赖于基数的分布情况而不依赖于键值 K K K的大小 O ( N lg ? N ) O(N\lg N) O(NlgN)。
- 5、基数交换排序不需要额外的链接。
还有一种情况要特别注意,就是计算机采取补码时,如果键值不是unsigned int类型,在最后处理时会有所不同。以
M
=
256
M=256
M=256为例,最后串起各堆的顺序应该为:
(
10000000
)
2
,
(
10000001
)
2
,
…
,
(
11111111
)
2
,
(
00000000
)
2
,
(
00000001
)
2
,
…
,
(
01111111
)
2
(10000000)_2,(10000001)_2,\ldots,(11111111)_2,(00000000)_2,(00000001)_2,\ldots,(01111111)_2
(10000000)2?,(10000001)2?,…,(11111111)2?,(00000000)2?,(00000001)2?,…,(01111111)2?