图的遍历

从已给的连通图中某一个顶点出发，沿着一些边访遍图中所有的顶点，且每个顶点仅被访问一次，就叫做图的遍历，它是图的基本运算

图的特点：图中可能存在回路，且图的任一顶点都可能与其它顶点相通，在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的节点

避免重复的方法：设置一个辅助的数组 visit[n]，用来标记每个被访问的顶点。

初始状态 visit[i] 为 0
顶点 i 被访问，改 visit[i] 为 1，防止被多次访问。

深度优先遍历(DFS)

Depth First Search

方法

在访问图中某一起始顶点 v 后，由 v 出发，访问它的任一邻接顶点 w1
在从 w1 出发，访问与 w1 邻接但还未被访问过得顶点 w2
再从 w2 出发，进行类似的访问…
如此进行下去，知道到达所有的邻接顶点都被访问过的顶点 u 为止
接着，退回一步，退到前一次刚访问过的顶点，看看是否还有其它没有被访问的邻接顶点
如果有，则访问此顶点，之后再从此顶点出发，进行与前述类似的访问
如果没有，就再退回一步进行搜索。重复上述过程，知道连通图中所有顶点都被访问过为止

示例

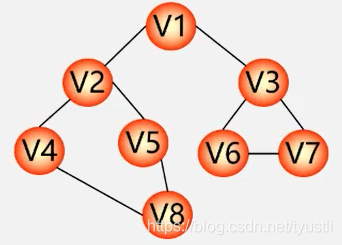
请添加图片描述

则它的深度优先遍历为

v1->v2->v4->v8->v5->v3->v6->v7
v1->v2->v4->v8->v5->v3->v7->v6
v1->v2->v5->v8->v4->v3->v7->v6
v1->v2->v5->v8->v4->v3->v6->v7
......

连通图的深度优先遍历类似图的先根遍历
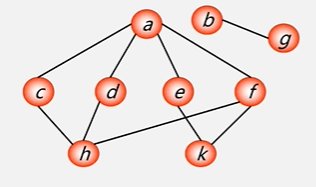
请添加图片描述

则它的深度优先遍历为

a->c->h->d->f->k->e->b->g

代码实现

采用邻接矩阵表示图的深度优先搜索遍历

void DFS(struct AMGraph G, int v) // 图 G 为邻接矩阵类型
{
    visit(v); // 访问第 v 个顶点
    visited[v] = true; // 标志位
    for(w = 0; w < G.vexnum; w++) // 依次检查邻接矩阵 v 所在的行
        if((G.arcs[v][w]!=0) && (!visited[w]))
            DFS(G, w); // w 是 v 的邻接点，如果 w 未访问，则递归调用 DFS
}

算法效率分析

时间复杂度：O(n2)

广度优先遍历(BFS)

Breadth First Search

方法

从图的某一个结点出发，首先依次访问该节点的所有邻接结点 v1,v2,v3…,再按这些顶点被访问的先后次序依次访问与他们相邻接的所有未被访问的顶点。

重复此过程，直至所有顶点均被访问为止

示例

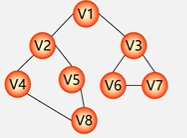
请添加图片描述
则它的广度优先遍历为

v1->v2->v3->v4->v5->v6->v7->v8

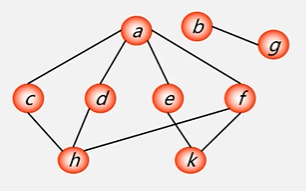
请添加图片描述

则它的广度优先遍历为

a->c->d->e->f->h->k->b->g

代码实现

按广度优先非递归遍历连通图 G

void BFSTraverse(struct ALGraph G, void (*Visit)(char *))
{
    int v, u, w;
    LinkQueue Q;
    for (v = 0; v < G.vexnum; ++v)
        visited[v] = FALSE;        // 置初值
    InitQueue(&Q);                 // 置空的辅助队列Q
    for (v = 0; v < G.vexnum; v++) // 如果是连通图，只v=0就遍历全图
        if (!visited[v])           // v尚未访问
        {
            visited[v] = TRUE;
            Visit(G.vertices[v].data);
            EnQueue(&Q, v);        // v入队列
            while (!QueueEmpty(Q)) // 队列不空
            {
                DeQueue(&Q, &u); // 队头元素出队并置为u
                for (w = FirstAdjVex(G, G.vertices[u].data); w >= 0; w = NextAdjVex(G, G.vertices[u].data, G.vertices[w].data))
                    if (!visited[w]) // w为u的尚未访问的邻接顶点
                    {
                        visited[w] = TRUE;
                        Visit(G.vertices[w].data);
                        EnQueue(&Q, w); // w入队
                    }
            }
        }
    printf("\n");
}