比赛网址:https://ac.nowcoder.com/acm/contest/19483
目录
? ??知识点:费马小定理
? ?思路:
? ?AC代码:
? ??AC代码:
? ??I题和J的思路:
? ??AC代码:
A:智乃酱的区间乘积(费马小定理)
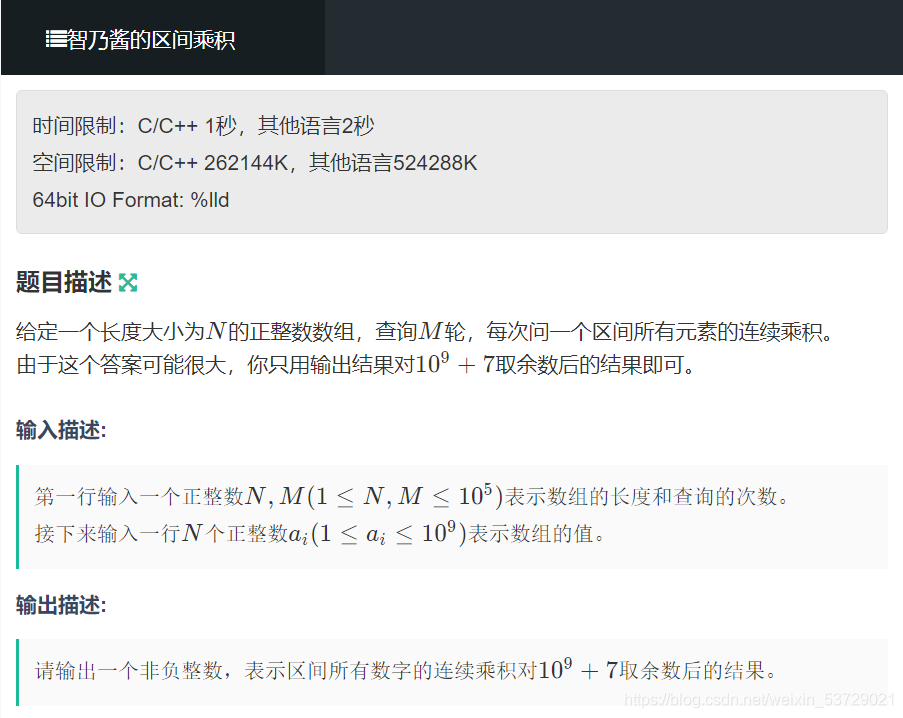
给定一个长度大小为N的正整数数组,查询M轮,每次问一个区间所有元素的连续乘积。
由于这个答案可能很大,你只用输出结果对1e9+7取余数后的结果即可。
 知识点:费马小定理
知识点:费马小定理
(a/b)%mod=a*pow(b,mod-2);
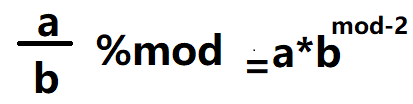 ?
?
?快速幂模板:
ll fp(ll x,ll y)
{
ll ans=1;
ll base=x;
while(y)
{
if(y&1) ans=ans*base%mod;
y>>=1;
base=base*base%mod;
}
return ans;
}思路:
求前缀积,再sum[j]/sun[i]*arr[i],处理除法时用上费马小定理和快速幂。
AC代码:
#include<iostream>
#include<cmath>
using namespace std;
typedef long long ll;
const int N=1e5+5;
const int mod=1e9+7;
ll n,m;
ll fac[N],inv[N];
ll fp(ll x,ll y)//快速幂模板
{
ll ans=1;
ll base=x;
while(y)
{
if(y&1) ans=ans*base%mod;
y>>=1;
base=base*base%mod;
}
return ans;
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
ll x,y;
fac[0]=inv[0]=1;
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>x;
fac[i]=fac[i-1]*x%mod;//记录前缀积
inv[i]=fp(fac[i],mod-2);//前i项的mod-2次方
}
while(m--)
{
cin>>x>>y;
cout<<fac[y]*inv[x-1]%mod<<endl;//费马小定理的应用
}
return 0;
}
G:牛牛的Link Power I:
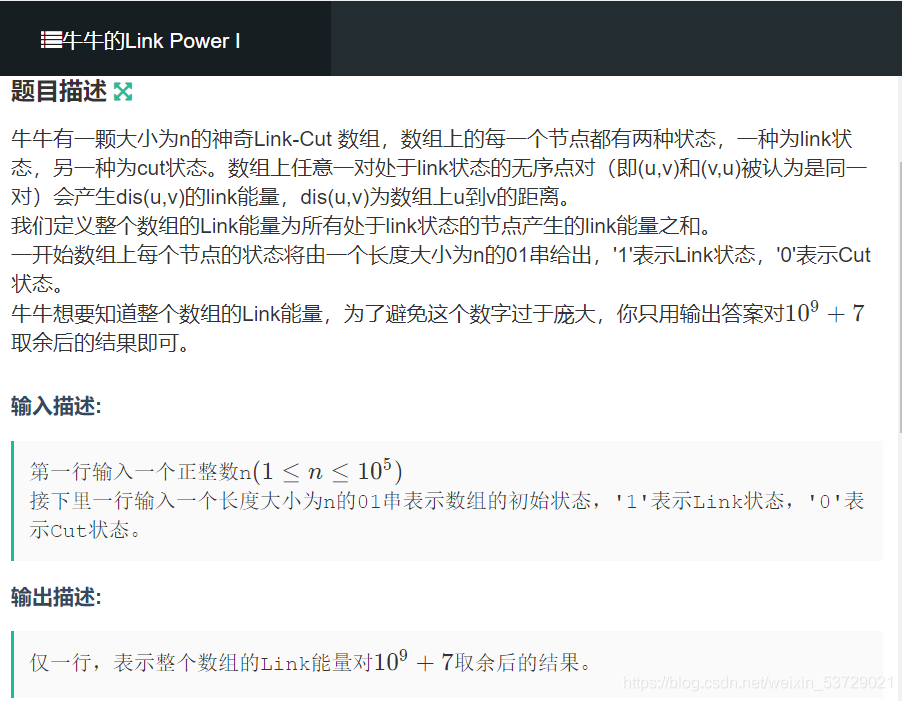
牛牛有一颗大小为n的神奇Link-Cut 数组,数组上的每一个节点都有两种状态,一种为link状态,另一种为cut状态。数组上任意一对处于link状态的无序点对(即(u,v)和(v,u)被认为是同一对)会产生dis(u,v)的link能量,dis(u,v)为数组上u到v的距离。
我们定义整个数组的Link能量为所有处于link状态的节点产生的link能量之和。
一开始数组上每个节点的状态将由一个长度大小为n的01串给出,'1'表示Link状态,'0'表示Cut状态。
牛牛想要知道整个数组的Link能量,为了避免这个数字过于庞大,你只用输出答案对10^9+7取余的结果即可。
 ?
?
 ?
?
?思路:
思维题。第i个1产生的能量是第i-1这个1的能量加上i与i-1之间的距离*i之前1的个数
其实知道第i-1个link点到其前面的所有link点的能量之和w(i-1),第i个link点到其前面所有link的能量之和则为w(i)=w(i-1)+num(前面的link点数)*(dis(i-1,i)[ i-1 到 i 的距离]),因为把乘法拆开来其实就是之前的每个dis都加上dis(i-1,i)则这个为第i个link点的前缀能量和,最后再O(n)扫一遍所有的前缀能量和即是答案。
?
AC代码:
#include<bits/stdc++.h>
using namespace std;
long long sum[200000];
long long s;
int n;
char a[200000];
int ans;
long long p = -1;
long long SUM;
const long long mood = 1e9 + 7;
int main(){
cin >> n;
cin >> a;
for (int i = 0; i < n; i ++){
ans ++;
if (a[i] == '1'){
p ++;
sum[i] = s + p * ans;
s = sum[i];
ans = 0;
}
}
for (int i = 0; i < n; i ++) SUM +=sum[i], SUM %= mood;
cout << SUM;
return 0;
}
I:[NOIP2013]积木大赛?
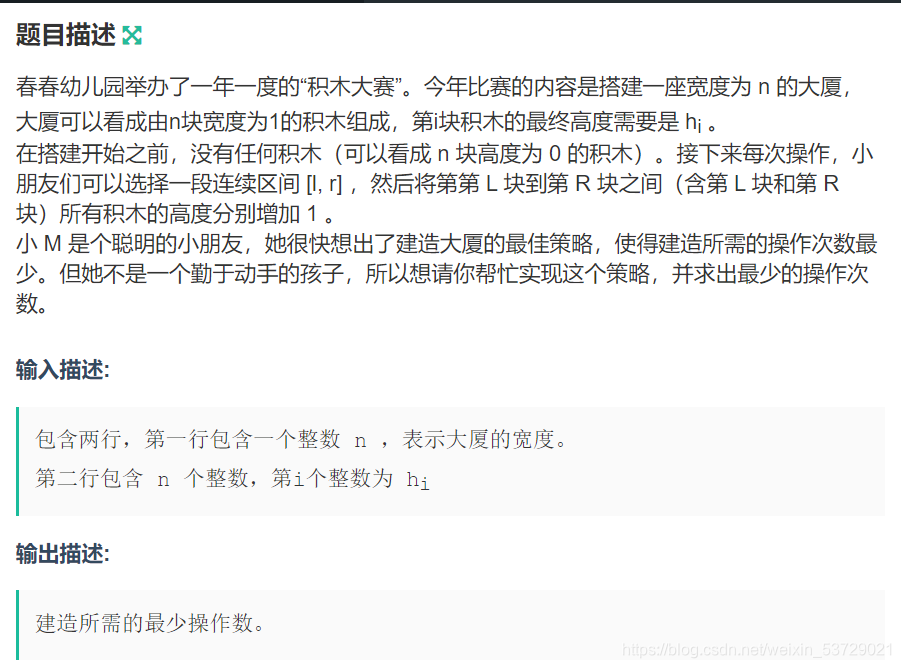
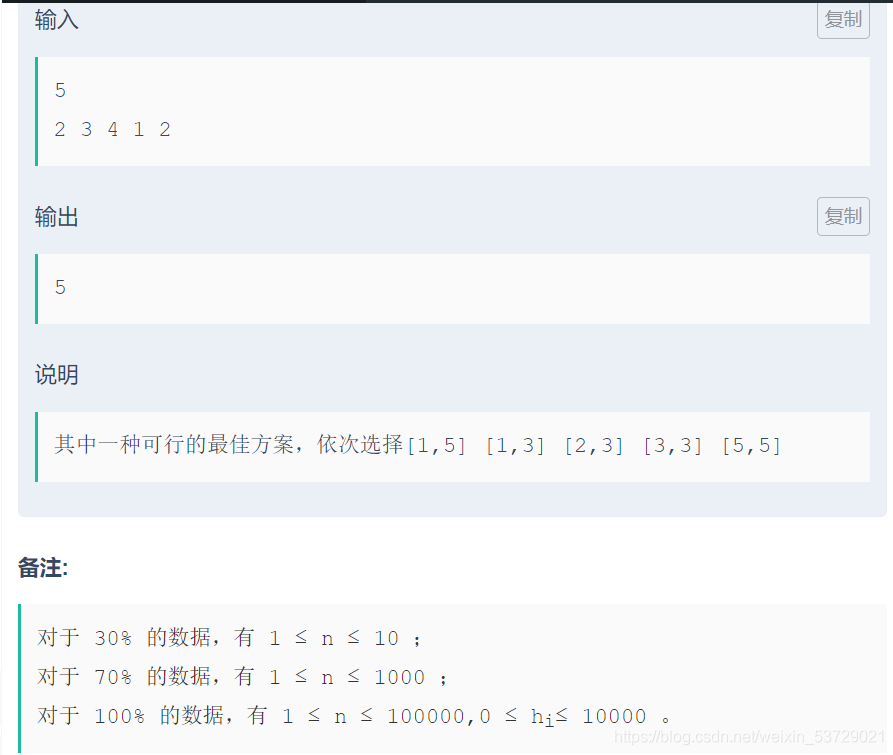
春春幼儿园举办了一年一度的“积木大赛”。今年比赛的内容是搭建一座宽度为 n 的大厦,大厦可以看成由n块宽度为1的积木组成,第i块积木的最终高度需要是 hi 。
在搭建开始之前,没有任何积木(可以看成 n 块高度为 0 的积木)。接下来每次操作,小朋友们可以选择一段连续区间 [l, r] ,然后将第第 L 块到第 R 块之间(含第 L 块和第 R 块)所有积木的高度分别增加 1 。
小 M 是个聪明的小朋友,她很快想出了建造大厦的最佳策略,使得建造所需的操作次数最少。但她不是一个勤于动手的孩子,所以想请你帮忙实现这个策略,并求出最少的操作次数。
J:[NOIP2018]道路铺设:
?
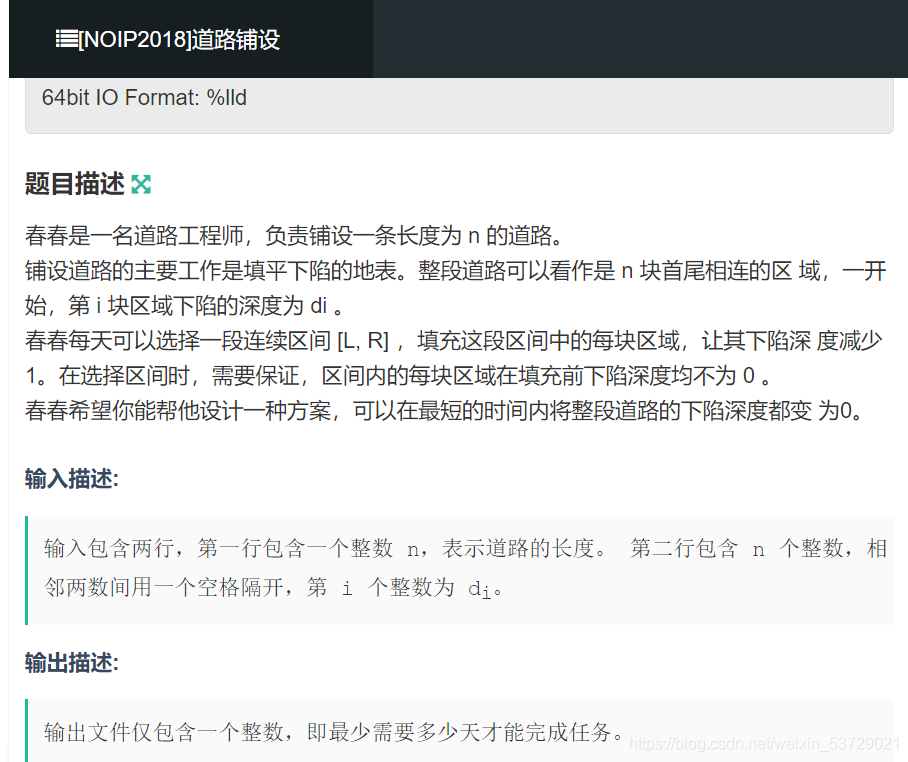
春春是一名道路工程师,负责铺设一条长度为 n 的道路。
铺设道路的主要工作是填平下陷的地表。整段道路可以看作是 n 块首尾相连的区 域,一开始,第 i 块区域下陷的深度为 di 。
春春每天可以选择一段连续区间 [L, R] ,填充这段区间中的每块区域,让其下陷深 度减少 1。在选择区间时,需要保证,区间内的每块区域在填充前下陷深度均不为 0 。
春春希望你能帮他设计一种方案,可以在最短的时间内将整段道路的下陷深度都变 为0。
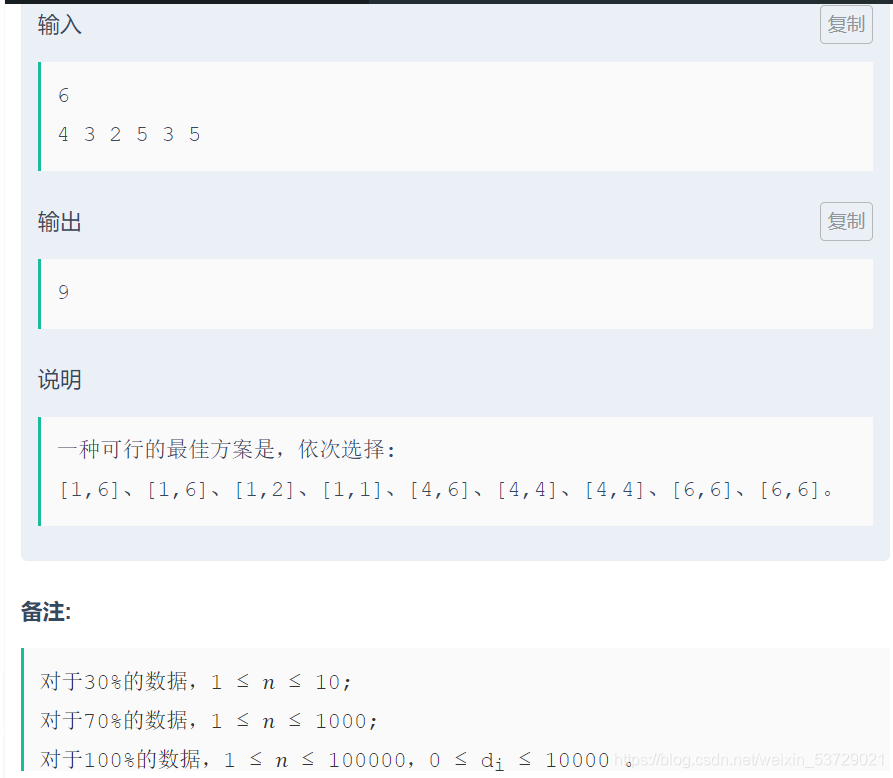
I题和J的思路:
这两题的思路是一样的,AC代码也一样,答案初始值为第一个数,以第一个数为基数,检查下一个数是否大于该数,若大于,答案再加上大于的那一部分,否则不变,再更新基数为这个数,继续余下一个数作比较,直到最后一个树,输出答案。
AC代码:
#include<cstdio>
using namespace std;
const int maxn=100000+10;
int a[maxn];
int main(){
int n;
scanf("%d",&n);
for (int i=0;i<n;i++) scanf("%d",&a[i]);
int now=a[0],ans=a[0];
for(int i=1;i<n;i++){
if (a[i]>now) ans+=(a[i]-now);
now=a[i];
}
for(int i=1;i<n;i++){
if(a[i]>now) ans=ans+(a[i]-now);
now=a[i];
}
printf("%d",ans);
return 0;
}