BST树区间元素搜索问题
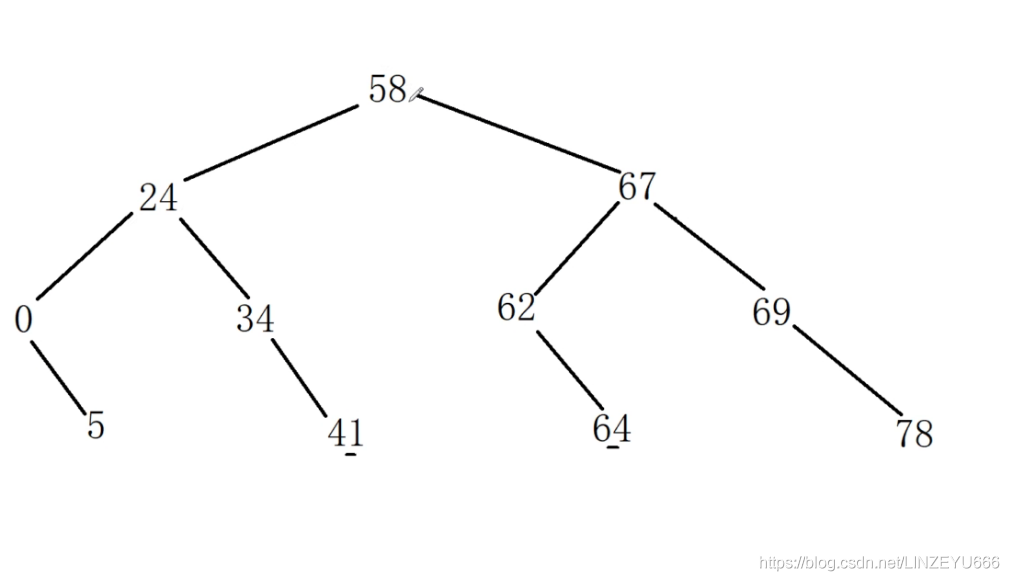
比如说,寻找10-70之间的所有元素
方法1: 遍历1遍,符合的打印出来。但是效率不高。
方法2:
利用中序遍历的升序的特点。
//求满足区间的元素值[i, j]
void findValues(vector<T>& vec, int i, int j)
{
findValues(root_, vec, i, j);
}
//求满足区间的元素值[i, j]实现
void findValues(Node* node, vector<T>& vec, int i, int j)
{
if (node != nullptr)
{
//在当前节点的左子树中搜索 LVR的方式,中序遍历
if (node->data_ > i)//比i小就不用去左子树搜索了
{
findValues(node->left_, vec, i, j);//执行L
}
if (node->data_ >= i && node->data_ <= j)//执行V
{
vec.push_back(node->data_);//存储满足区间元素的值
}
//在当前节点的右子树中搜索
if (node->data_ < j)//比j大就不用去右子树搜索了
{
findValues(node->right_, vec, i, j);//执行R
}
}
}
判断一棵树是不是BST树
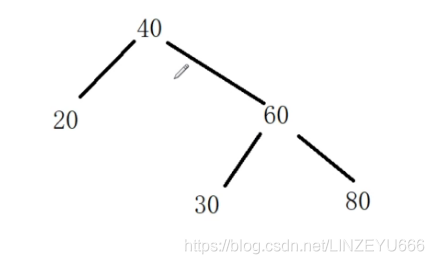
要考虑到上图这种情况来实现代码
利用BST树的中序遍历是从小到大升序的思想
//判断二叉树是否是BST树
bool isBSTree()
{
Node* pre = nullptr;//用来记录中序遍历前一个节点的值,一直要更新的
return isBSTree(root_, pre);
}
//判断二叉树是否是BST树的实现 利用BST树中序遍历是一个升序的特点
bool isBSTree(Node* node, Node*& pre)
{
if (node == nullptr)
{
return true;
}
if (!isBSTree(node->left_, pre))//L主要判断使递归结束的条件
{
return false;
}
//V
if (pre != nullptr)
{
if (comp_(node->data_, pre->data_))
//当前节点的值小于前一个节点的值。主要判断使递归结束的条件
{
return false;
}
}
pre = node;//更新中序遍历的前驱节点
return isBSTree(node->right_, pre);//R
}
判断二叉树子树问题
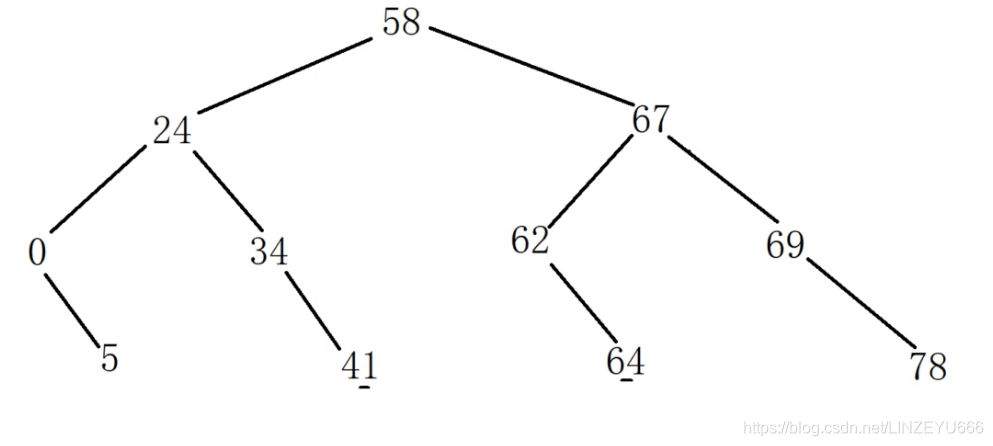
判断下面这个小树是不是上面这棵大树的子树
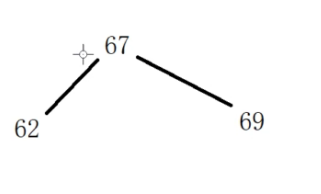
先在大树中找到这个小树的根节点67
然后大树和小树同时往左走往右走遍历
遍历到的值必须是相同的
大树里的可以多,但不能少。
//判断子树问题
bool isChildTree(BSTree<T, Comp>& child)
{
// 在当前二叉树上找child的根节点
if (child.root_ == nullptr)
{
return true;
}
Node* cur = root_;
while (cur != nullptr)
{
if (cur->data_ == child.root_->data_)//树的节点与子树的根节点值相等
{
break;
}
else if (comp_(cur->data_, child.root_->data_))//当前节点的值小于子树的根节点的值
{
cur = cur->right_;
}
else//当前节点的值大于子树的根节点的值
{
cur = cur->left_;
}
}
if (cur == nullptr)
{
return false;//没有找到子树的根,不匹配
}
return isChildTree(cur, child.root_);
}
//判断子树问题实现
bool isChildTree(Node* father, Node* child)
{
if (father == nullptr && child == nullptr)
{
return true;
}
if (father == nullptr)//子树里面有的节点,当前二叉树没有
{
return false;
}
if (child == nullptr)
{
return true;
}
//判断值不相同
if (father->data_ != child->data_)// V 对应的值不相同
{
return false;
}
return isChildTree(father->left_, child->left_)// L 左右孩子同时进行判断
&& isChildTree(father->right_, child->right_);// R
}
求LCA最近公共祖先节点
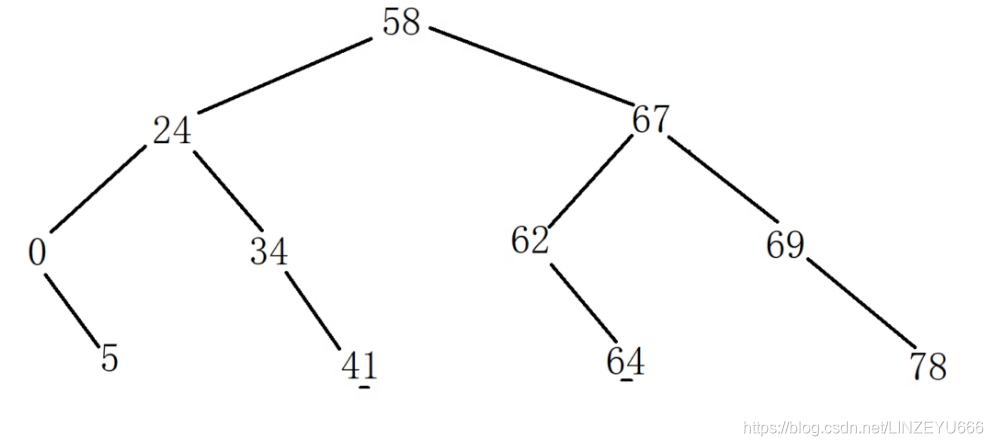
比如说24和67,最近公共祖先节点就是58,
32和64,最近公共祖先节点就是58
5和41的最近公共祖先节点就是24
62和64的最近公共祖先节点就是62
怎么判断5和41的最近公共祖先节点是24,而不是58?
我们看,5和41都比58小,说明都在58的左子树,58就肯定不是它们的最近公共祖先节点。最近公共祖先节点肯定是大于一个数而小于另一个数。
搜索的时候值等于要比较的节点值,就是在一条分枝上。
//最近公共祖先节点
int getLCA(int val1, int val2)
{
Node* node = getLCA(root_, val1, val2);
if (node == nullptr)//没找到
{
throw "no LCA!";
}
else
{
return node->data_;
}
}
//最近公共祖先节点实现
Node* getLCA(Node* node, int val1, int val2)
{
if (node == nullptr)
{
return nullptr;
}
if (comp_(node->data_, val1) && comp_(node->data_, val2))//当前节点的值小于val1和val2
{
return getLCA(node->right_, val1, val2);
}
else if (comp_(val1, node->data_) && comp_(val2, node->data_))//当前节点的值大于val1和val2
{
return getLCA(node->left_, val1, val2);
}
else//一个大于一个小于。就是最近公共祖先节点。
{
return node;
}
}
二叉树镜像翻转问题
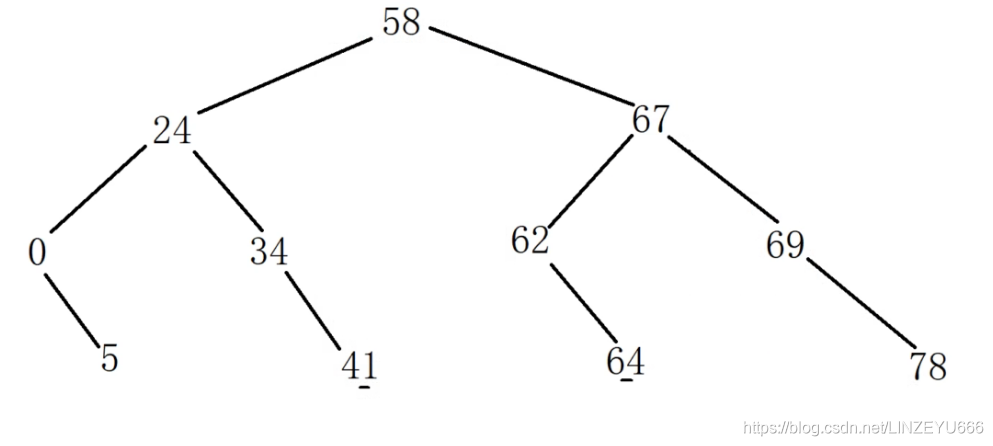
相当于有一面镜子
翻转。
78就是在最左边
0就是在最右边
相当于根节点进行遍历,把左右的节点交换就可以了。
//镜像翻转
void mirror01()
{
mirror01(root_);
}
//镜像翻转
void mirror01(Node* node)
{
if (node == nullptr)
return;
//前序遍历
//V
Node* tmp = node->left_;
node->left_ = node->right_;
node->right_ = tmp;//交换节点
mirror01(node->left_);//L操作
mirror01(node->right_);//R操作
}
二叉树的镜像对称
就是在根节点放一面镜子
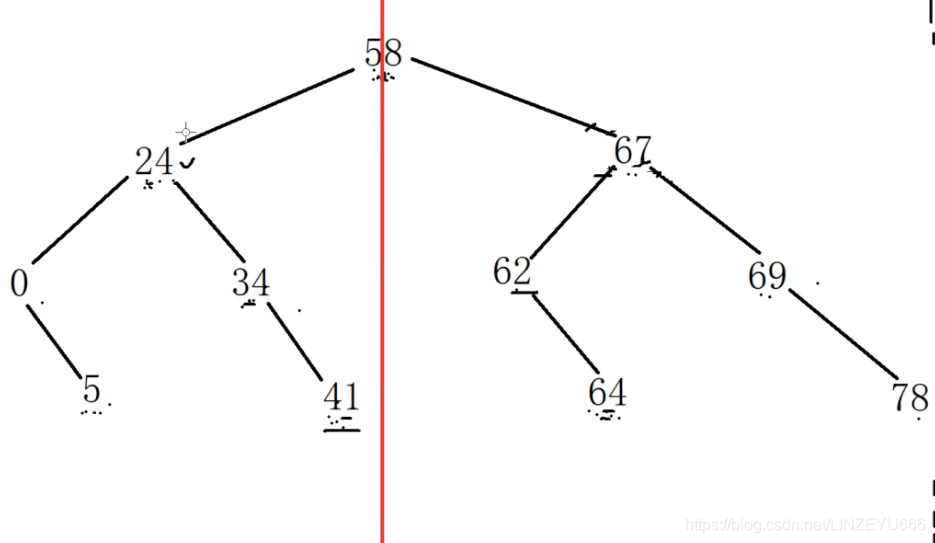
看左子树和右子树是不是对称,就是左右对应节点的值相等不相等。
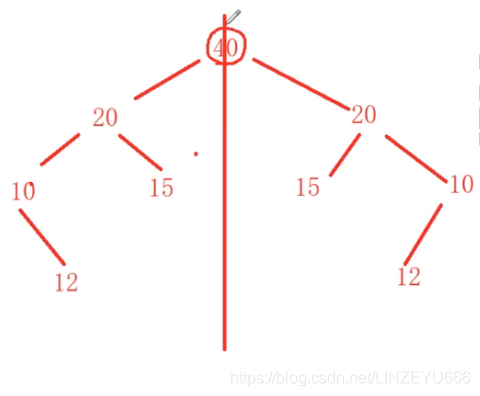
//镜像对称
bool mirror02()
{
if (root_ == nullptr)
return true;
return mirror02(root_->left_, root_->right_);
}
//镜像对称
bool mirror02(Node* node1, Node* node2)
{
if (node1 == nullptr && node2 == nullptr)
{
return true;
}
if (node1 == nullptr || node2 == nullptr)
{
return false;
}
if (node1->data_ != node2->data_)
{
return false;
}
return mirror02(node1->left_, node2->right_)
&& mirror02(node1->right_, node2->left_);
}
已知BST树的前序遍历和中序遍历,重建BST树
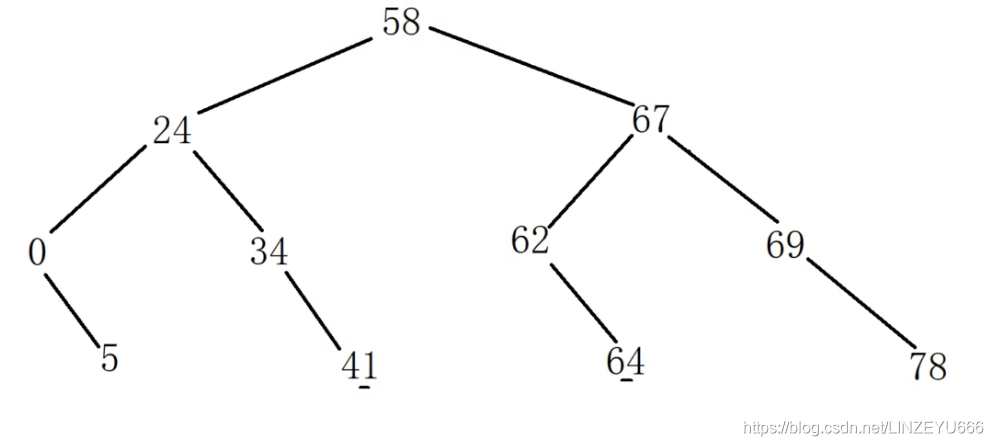

前序遍历是VLR,中序遍历是LVR,
所以说
前序遍历的第一个数字58就是根节点!!!
但是58的左子树和右子树都有哪些节点?
中序遍历的58的左边数字就是根节点的左子树,58的右边数字就是根节点的右子树
我们拿前序遍历的第一个数字,58,也就是根节点。
然后拿这个数值去中序遍历里面找。第k个位置。
m到k-1就是根节点58的右子树的节点

根节点的左子树的节点个数:k-m
那58的左子树的前序遍历是什么呢?
58的左子树的前序遍历的下标就是从i+1开始到 i+(k-m)
那它们的根就是下标为i+1的元素,即24
然后拿24在中序遍历里找。
24的左边就是它的左子树。就是 0,5
右子树就是34,41
创建根的右子树就是从k+1到n

//重建二叉树
void rebuild(int pre[], int i, int j, int in[], int m, int n)//前序,中序,起始,末尾下标
{
root_ = _rebuild(pre, i, j, in, m, n);
}
//重建二叉树递归实现
Node* _rebuild(int pre[], int i, int j, int in[], int m, int n)
{
if (i > j || m > n)//已经遍历完了
{
return nullptr;
}
//创建当前子树的根节点
Node* node = new Node(pre[i]);//拿前序的第一个数字创建子树根节点 V
for (int k = m; k <= n; ++k)
{
if (pre[i] == in[k])//在中序遍历中找子树根节点的下标k
{
node->left_ = _rebuild(pre, i + 1, i + (k - m), in, m, k - 1);// L
node->right_ = _rebuild(pre, i + (k - m) + 1, j, in, k + 1, n);// R
return node;
}
}
return node;
}
判断一棵BST树是否是平衡树
任意节点的左右子树的高度差不超过1(0,1,-1)
在回溯的时候检测,比较好。
LRV
//判断平衡树
bool isBalance()
{
int l = 0;
bool flag = true;
isBalance02(root_, l, flag);
return flag;
}
//判断平衡树 效率比较低,遍历的次数太多了
bool isBalance(Node* node)
{
if (node == nullptr)
return true;
if (!isBalance(node->left_))//L
return false;
if (!isBalance(node->right_))//R
return false;
int left = high(node->left_);
int right = high(node->right_);
return abs(left - right) <= 1;//V
}
//判断平衡树 效率高 递归过程中,记录了节点的高度值 ,返回节点高度值
int isBalance02(Node* node, int l, bool& flag)
{
if (node == nullptr)
{
return l;
}
int left = isBalance02(node->left_, l + 1, flag);//L
if (!flag)
return left;
int right = isBalance02(node->right_, l + 1, flag);//R
if (!flag)
return right;
//V
if (abs(left - right) > 1)//节点失衡了
{
flag = false;
}
return max(left, right);
}
求中序遍历倒数第k个节点
VLR
我们用VRL就是正数第k个
//求中序倒数第K个节点
int getVal(int k)
{
Node* node = getVal(root_, k);
if (node == nullptr)
{
string err = "no No.";
err += k;
throw err;
}
else
{
return node->data_;
}
}
//求中序倒数第K个节点
int i = 1;
Node* getVal(Node* node, int k)
{
if (node == nullptr)
return nullptr;
Node* left = getVal(node->right_, k); // R
if (left != nullptr)
return left;
//V
if (i++ == k)//在VRL的顺序下,找到正数第k个元素
{
return node;
}
return getVal(node->left_, k);//L
}
BST树的析构函数
//层序遍历思想释放BST树所有节点资源
~BSTree()//析构函数
{
if (root_ != nullptr)
{
queue<Node*> s;
s.push(root_);//根节点入队
while (!s.empty())
{
Node* front = s.front();//获取队头
s.pop();//出队
if (front->left_ != nullptr)
{
s.push(front->left_);
}
if (front->right_ != nullptr)
{
s.push(front->right_);
}
delete front;
}
}
}