[数据结构与算法]16. 堆

堆

由于堆的存储使用到了数组的存储二叉树的方式，所以我们先介绍二叉树的顺序存储

1. 二叉树的顺序存储

1.1 存储方式

使用数组保存二叉树结构，即将二叉树用层序遍历方式放入数组中。

一般只适合表示完全二叉树，因为非完全二叉树会有空间的浪费。

这种方式的主要用法就是堆的表示。

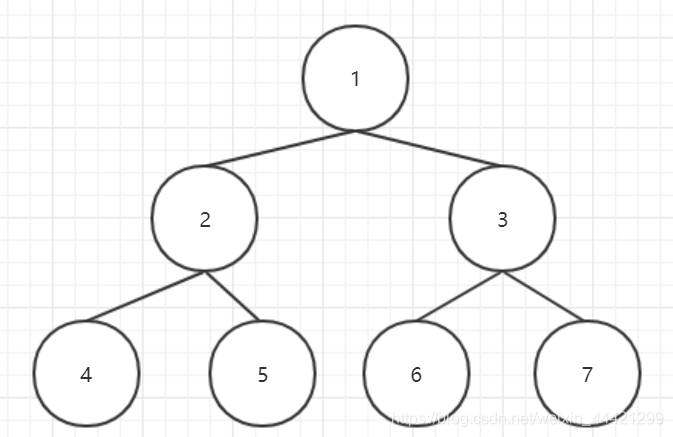
如上图，其顺序存储的结果为：

1.2 数组中的下标关系

通过观察上面的例子，我么可以发现

• 父节点(parent)的数组下标=（孩子节点(child)下标-1）/2

例：父节点 2 的 下标为1 ，其左孩子 4 的下标 （3-1）/2 = 1 其右孩子 5 的下标 （4-1）/2 = 1

• 左孩子节点下标=父节点下标*2+1

例：父节点3 下标为2 ，其左孩子6的下标为5 2*2+1=5

• 右孩子节点下标=父节点下标*2+1

例：父节点3 下标为2 ，其右孩子7的下标为6 2*2+2=5

2. 堆的概念

**堆是一种满足以下条件的树：**堆中的每一个节点值都大于等于（或小于等于）子树中所有节点的值。或者说，任意一个节点的值都大于等于（或小于等于）所有子节点的值。

1. 堆逻辑上是一棵完全二叉树

2. 堆物理上是保存在数组中

3. 满足任意结点的值都大于其子树中结点的值，叫做大堆，或者大根堆，或者最大堆

4. 反之，则是小堆，或者小根堆，或者最小堆

5. 堆的基本作用是，快速找集合中的最值

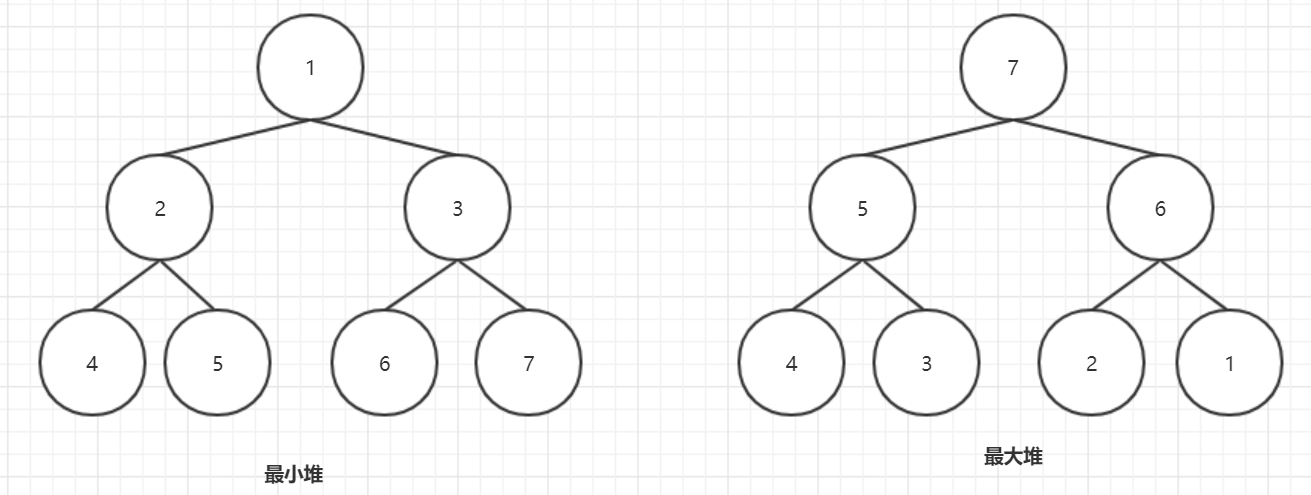
最大堆总是将其中的最大值存放在树的根节点。而对于最小堆，根节点中的元素总是树中的最小值。堆属性非常有用，因为堆常常被当做优先队列使用，因为可以快速地访问到“最重要”的元素。

3. 堆的操作

**前提：**左右子树必须已经是一个堆，才能堆化。

3.1向下堆化（以构建小根堆为例）

如果我们要将 节点9 调整到正确的位置，首先应该找到其左右孩子的较小值( 节点2 )，将其与 节点9 调换位置，接着以交换后的新位置为根节点再次判断调整，找到其左右孩子的较小值( 节点6 )，将其与 节点9 调换位置，最终结果如下图所示

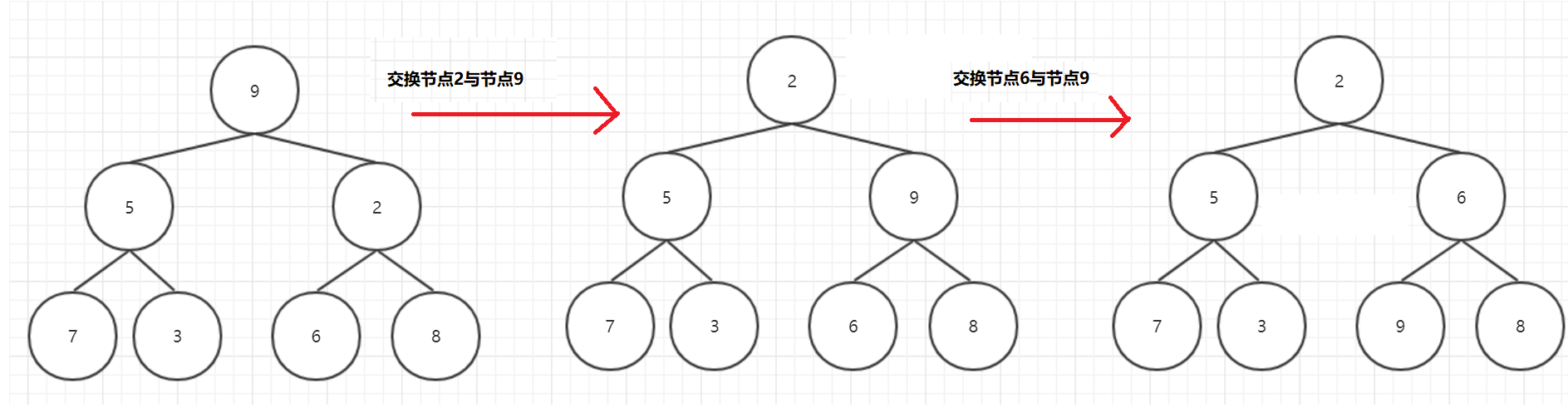
代码如下

/**
     * 向下调整堆 （小根堆）
     * @param array 堆元素数组
     * @param size 通过size指定array数组中哪些元素是有效堆元素
     * @param index 从哪个位置开始调整
     */
public static void shiftDown(int[] array, int size, int index)
{
    int parent = index;
    int child = 2 * parent + 1;//左子树下标
    while (child < size)
    {
        //比较左右子树，找到较小值
        if (child + 1 < size && array[child + 1] < array[child])
        {
            child = child + 1;
        }
        //将child与parent比较
        if (array[child] < array[parent])
        {
            //如果父节点大于子节点，交换其位置
            int temp = array[child];
            array[child] = array[parent];
            array[parent] = temp;
        }
        else
        {
            //无需调整
            break;
        }
        //更新
        parent = child;
        child = parent * 2 + 1;
    }
}

3.2 向上堆化（以构建大根堆为例）

如果我们要将 **节点10 ** 调整到正确的位置，判断其 父节点7 与它的大小，如果其大于父节点值，则交换两个节点，交换后以的新位置为孩子节点依次判断调整，具体步骤如下图所示

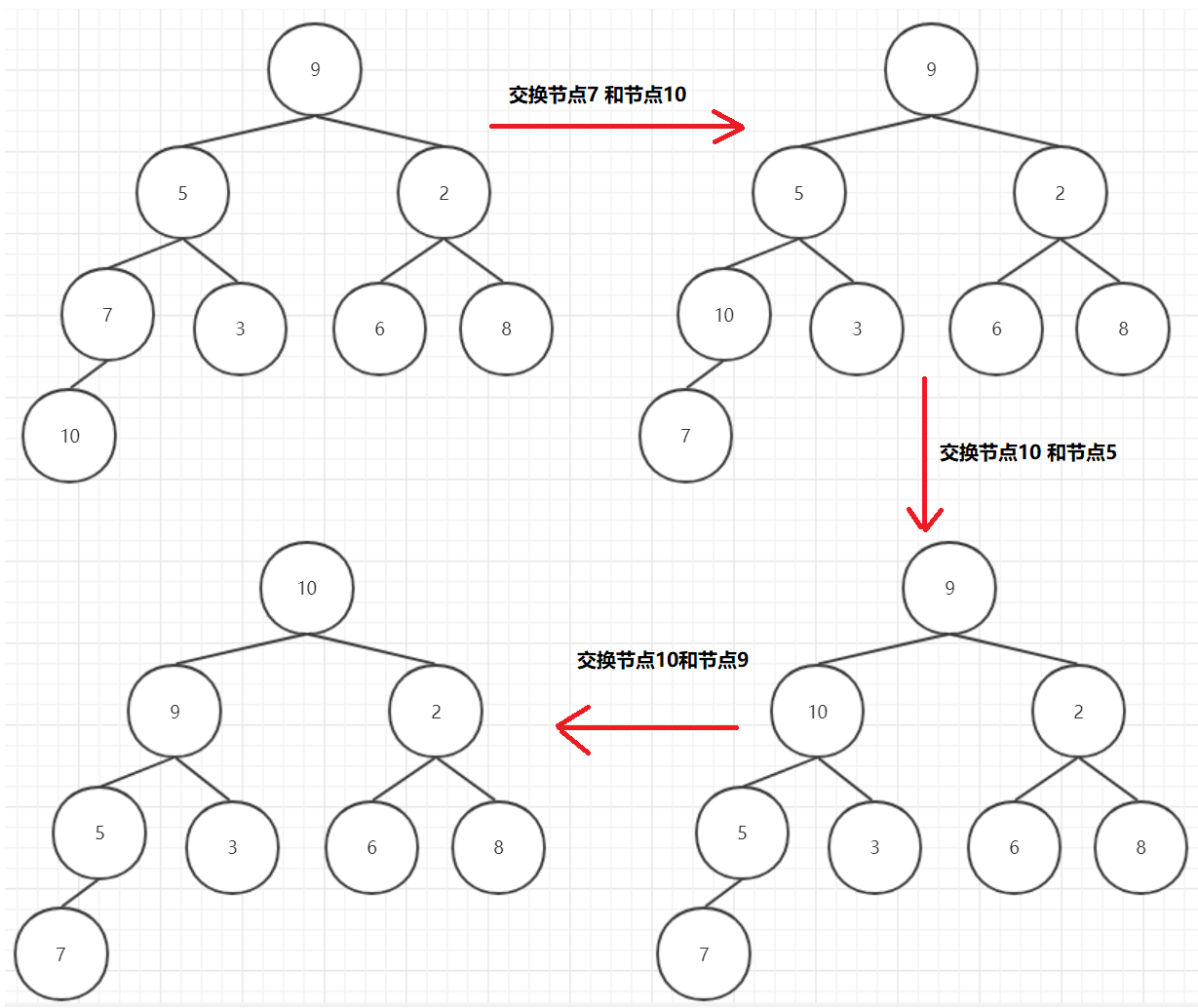
代码

/**
     * 向上建堆（大顶堆）
     * @param array
     * @param index
     */
    public static void shiftUp(int array[], int index)
    {
        int child = index;
        int parent = (index - 1) / 2;//父节点为 （孩子节点下标位置-1） /2
        while (child > 0)
        {
            //将child与parent比较，如果孩子节点大于父节点，则交换位置
            if (array[child] > array[parent])
            {
                int temp = array[child];
                array[child] = array[parent];
                array[parent] = temp;
            }
            else
            {
                break;
            }
            //当前父节点位置作为新的孩子节点，递归下次
            child = parent;
            parent = (child - 1) / 2;
        }
    }

4. 优先队列

4.1 定义

普通的队列是一种先进先出的数据结构，元素在队列尾追加，而从队列头删除。在优先队列中，元素被赋予优先级。当访问元素时，具有最高优先级的元素最先删除。优先队列具有最高级先出 （first in, largest out）的行为特征。通常采用堆数据结构来实现。

4.2 实现

通过上面对堆的学习，我们发现构建堆后 可以快速地访问到**“最重要”**的元素 ，所以我们用其来实现优先队列。

• 在入队列时，使用向上堆化
• 在出队列时，用最后一个元素覆盖第堆顶元素，再使用向下堆化

public class MypPriorityQueue
{
    //存储堆(二叉树)的数组
    private int array[] = new int[100];
    //当前队列中的元素个数
    private int size = 0;

    /**
     * 测试方法
     * @param args
     */
    public static void main(String[] args)
    {
        MypPriorityQueue queue = new MypPriorityQueue();
        queue.offer(9);
        queue.offer(5);
        queue.offer(2);
        queue.offer(7);
        queue.offer(3);
        queue.offer(6);
        queue.offer(8);
        for (int i = 0; i < 7; i++)
        {
            System.out.println(queue.poll());
        }
    }

    /**
     * 向上建堆（大顶堆）
     * @param array
     * @param index
     */
    public void shiftUp(int array[], int index)
    {
        int child = index;
        int parent = (index - 1) / 2;
        while (child > 0)
        {
            if (array[child] > array[parent])
            {
                int temp = array[child];
                array[child] = array[parent];
                array[parent] = temp;
            }
            else
            {
                break;
            }
            child = parent;
            parent = (child - 1) / 2;
        }
    }

    /**
     * 向下建堆（大顶堆）
     * @param array
     * @param size
     * @param index
     */
    public void shiftDown(int[] array, int size, int index)
    {
        int parent = index;
        int child = 2 * index + 1;//左子树
        while (child < size)
        {
            if (child + 1 < size && array[child] < array[child + 1])
            {
                child = child + 1;
            }
            if (array[parent] < array[child])
            {
                int temp = array[parent];
                array[parent] = array[child];
                array[child] = temp;
            }
            else
            {
                break;

            }
            parent = child;
            child = 2 * parent + 1;
        }
    }

    /**
     * 入队列
     * @param x
     */
    public void offer(int x)
    {
        array[size] = x;
        size++;
        //将新加入元素调整位置
        shiftUp(array, size - 1);
    }

    /**
     * 出队列
     * @return
     */
    public int poll()
    {
        //要出队列的元素为数组中第一个元素
        int oldValue = array[0];
        //但是为了保证堆结构，不能直接返回
        //先用最后一个元素覆盖堆顶元素
        array[0] = array[size - 1];
        //由于最后一个元素已经存到了堆顶，直接删除
        size--;
        //接着从下调整，重新构建堆,从0开始
        shiftDown(array, size, 0);
        return oldValue;
    }
}

4.3 类库中的优先队列

Java类库中已经给我们提供了优先队列，我们在日后可以直接使用

import java.util.PriorityQueue;

public static void main(String[] args)
{
    //调用类库中的优先队列，直接创建对象
    PriorityQueue<Integer> queue = new PriorityQueue<>();
    queue.offer(9);
    queue.offer(5);
    queue.offer(2);
    queue.offer(7);
    queue.offer(3);
    queue.offer(6);
    queue.offer(8);
    for (int i = 0; i < 7; i++)
    {
        System.out.println(queue.poll());
    }
}