[数据结构与算法]决战前端算法 — 排序算法 — 归并排序

本系列索引

• 线性表基础
  • 链表
  • 队列
  • 栈
• 树结构基础
  • 二叉树
  • 堆与优先队列
  • 并查集
• 排序算法
  • 快速排序
  • 归并排序
• 未完待续…

归并排序原理

归并排序，顾名思义，先有向下拆分，再有向上合并

以升序排序为例，首先我们将原数组拆分成两份，然后定义一个新数组和两个指针指向拆分后的两个数组，当左边数组指针指向的值比右边的小的时候就将其放入新数组中，否则就将右边的放入新数组中，如此操作直到双指针遍历完毕

归并排序的作用

这个算法可以用来处理大数据，比如说现有内存2GB，如何对40GB大小的文件进行升序排序？

首先我们可以将这个大文件拆分成20份2GB的小文件，然后进行20路归并。

每次从20个值中选出最大值，这个操作可以用小根堆完成。

由于数组temp 可以放在外部的硬盘中，因此归并排序和快速排序相比，归并排序是一种外部排序。

相关习题

剑指 Offer 51 数组中的逆序对

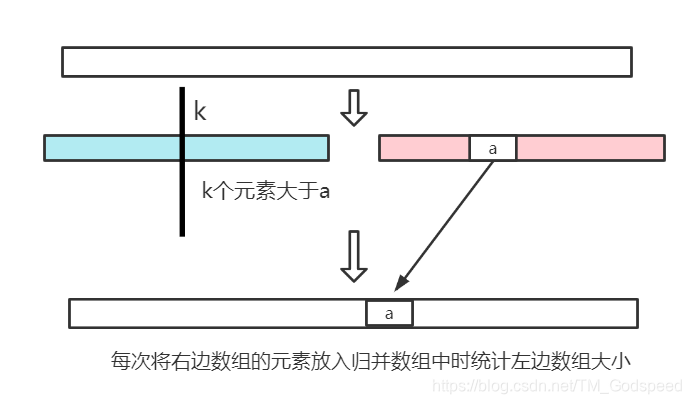
function counter(nums: number[], l: number, r: number) {
  if (l >= r) return 0
  const mid = (l + r) >> 1
  let res = 0, p1 = l, p2 = mid + 1
  res += counter(nums, l, mid)
  res += counter(nums, mid + 1, r)
  const temp: number[] = []
  while (p1 <= mid || p2 <= r) {
    if (p2 > r || (p1 <= mid && nums[p1] > nums[p2])) {
      temp.push(nums[p1++])
      res += r - p2 + 1
    } else {
      temp.push(nums[p2++])
    }
  }
  for (let i = l; i <= r; i++) nums[i] = temp[i - l]
  
  return res
}

function reversePairs(nums: number[]): number {
  return counter(nums, 0, nums.length - 1)
}

leetCode 148 排序链表

这道题解法和数组排序类似，只是由于链表不能直接获取链表长度，所以对归并函数新增一个参数用于表示链表长度，方便我们对链表拆成两份

function mergeSort(head: ListNode | null, len: number) {
  if (!head || !head.next) return head
  const mid = len >> 1
  let p = head
  for (let i = 1; i < mid; i++) p = p.next
  const temp = p
  p = p.next
  temp.next = null
  const lList = mergeSort(head, mid), rList = mergeSort(p, len - mid)
  // 合并
  const vHead = new ListNode()
  let p1 = lList, p2 = rList
  p = vHead
  while (p1 || p2) {
    if (!p2 || (p1 && p1.val < p2.val)) {
      p.next = p1
      p1 = p1.next
    } else {
      p.next = p2
      p2 = p2.next
    }
    p = p.next
  }
  p.next = null
  return vHead.next
}

function sortList(head: ListNode | null): ListNode | null {
  if (!(head && head.next)) return head
  let len = 0, p = head
  while (p) {
    len++
    p = p.next
  }
  return mergeSort(head, len)
}

leetCode 1305 两颗二叉搜索树中的所有元素

在二叉树一章提过，二叉搜索树的中序遍历就是一个升序数组，所以这题我们先对两颗二叉搜索树进行中序遍历，再进行合并

function median(root: TreeNode | null, ans: number[]) {
  if (!root) return root
  median(root.left, ans)
  ans.push(root.val)
  median(root.right, ans)
}

function getAllElements(root1: TreeNode | null, root2: TreeNode | null): number[] {
  const arr1: number[] = [], arr2: number[] = [], ans: number[] = []
  median(root1, arr1)
  median(root2, arr2)
  let p1 = 0, p2 = 0
  while (p1 < arr1.length || p2 < arr2.length) {
    if (p2 >= arr2.length || (p1 < arr1.length && arr1[p1] < arr2[p2])) {
      ans.push(arr1[p1++])
    } else {
      ans.push(arr2[p2++])
    }
  }
  return ans
}

leetCode 347 区间和的个数

这个地方用到了前面文章提到的前缀和数组，要计算区间和我们只要计算前缀和数组的差值就行了

根据题意我们的前缀和数组要符合的条件是
$$lower\le sum[j]?sum[i]\le upper(i<j)$$

let _lower: number, _upper: number, temp: number[] = []
function countTwoParts(nums: number[], l1: number, r1: number, l2: number, r2: number) {
  let ans = 0
  for (let a = l1, b = l1, i = l2; i <= r2; i++) {
    while (a <= r1 && nums[i] - nums[a] > _upper) a++
    while (b <= r1 && nums[i] - nums[b] >= _lower) b++
    ans += b - a
  }
  return ans
}

function mergeSort(arr: number[], l: number, r: number) {
  if (l >= r) return 0
  let ans = 0
  const mid = (l + r) >> 1
  ans += mergeSort(arr, l, mid)
  ans += mergeSort(arr, mid + 1, r)
  ans += countTwoParts(arr, l, mid, mid + 1, r)
  let p1 = l, p2 = mid + 1, k = l
  while (p1 <= mid || p2 <= r) {
    if (p2 > r || (p1 <= mid && arr[p1] < arr[p2])) {
      temp[k++] = arr[p1++]
    } else {
      temp[k++] = arr[p2++]
    }
  }
  for (let i = l; i <= r; i++) arr[i] = temp[i]
  return ans
}

function countRangeSum(nums: number[], lower: number, upper: number): number {
  const sum = [0]
  nums.forEach((num, i) => sum.push(num + sum[i]))
  _lower = lower, _upper = upper, temp = new Array(sum.length).fill(0)
  return mergeSort(sum, 0, sum.length - 1)
}

leetCode 315 计算右侧小于当前元素的个数

首先定义一种数据结构 [val: number, ind: number, cnt: number]，用于存储原数组的值、下标和题目所求数量(初始为0)，归并的时候根据原数组的值来排，在合并的时候对 cnt 进行操作，最后根据下标还原元素在原数组的位置并输出 cnt

type dataType = [val: number, ind: number, cnt: number]
function mergeSort(data: dataType[], l: number, r: number) {
  if (l >= r) return
  const mid = (l + r) >> 1, temp: dataType[] = []
  mergeSort(data, l, mid)
  mergeSort(data, mid + 1, r)
  let p1 = l, p2 = mid + 1
  while (p1 <= mid || p2 <= r) {
    if (p2 > r || (p1 <= mid && data[p1][0] > data[p2][0])) {
      data[p1][2] += r - p2 + 1
      temp.push(data[p1++])
    } else {
      temp.push(data[p2++])
    }
  }
  for (let i = l; i <= r; i++) data[i] = temp[i - l]
}

function countSmaller(nums: number[]): number[] {
  const data: dataType[] = [], ans: number[] = []
  nums.forEach((num, i) => data.push([num, i, 0]))
  mergeSort(data, 0, data.length - 1)
  data.forEach(d => ans[d[1]] = d[2])
  return ans
}

53 最大子序和

到现在为止，说到区间和，我们应该就要想到前序和了，这题也是用前序和数组来解，在遍历前序和的时候我们只要维护前序和数组的最小值即可

function maxSubArray(nums: number[]): number {
  const sums = [0]
  nums.forEach((num, i) => sums.push(num + sums[i]))
  let ans = sums[1]
  for (let i = 1, pre = 0; i < sums.length; i++) {
    ans = Math.max(sums[i] - pre, ans)
    pre = Math.min(pre, sums[i])
  }
  return ans
}

复习

leetCode 23 合并K个升序链表

这题使用堆来解

首先将所有链表压入小顶堆，定义虚拟头节点和移动指针P，然后当栈不为空时一直弹出堆顶元素并连接在新链表后，如果弹出的节点有下一位则将下一位节点继续压入堆

type dataType = ListNode | null
class SmallHeap {
  data: dataType[]
  constructor(data: dataType[]) {
    this.data = data
    this.init()
  }
  
  init() {
    for (let i = 0; i < this.data.length; i++) {
      if (!this.data[i]) {
        this.data.splice(i, 1)
        i--
      }
      this.sortUp(i)
    }
  }
  
  push(val: dataType) {
    this.data.push(val)
    this.sortUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    let ret: dataType
    if (this.data.length === 1) {
      ret = this.data.pop()
    } else {
      ret = this.data[0]
      this.data[0] = this.data.pop()
      this.sortDown(0)
    }
    if (ret.next) this.push(ret.next)
    return ret
  }
  
  sortUp(index: number) {
    let parentIndex: number
    while (index > 0) {
      parentIndex = (index - 1) >> 1
      if (this.data[index].val < this.data[parentIndex].val) {
        this.swap(index, parentIndex)
      } else {
        return
      }
      index = parentIndex
    }
  }
  
  sortDown(index: number) {
    let target: number, lIndex: number, rIndex: number
    while (index < this.data.length) {
      target = index, lIndex = (index << 1) + 1, rIndex = (index << 1) + 2
      if (lIndex < this.data.length && this.data[lIndex].val < this.data[target].val) {
        target = lIndex
      }
      if (rIndex < this.data.length && this.data[rIndex].val < this.data[target].val) {
        target = rIndex
      }
      if (target === index) return
      this.swap(index, target)
      index = target
    }
  }
  
  swap(a: number, b: number) {
    [this.data[a], this.data[b]] = [this.data[b], this.data[a]]
  }
  
  size() {
    return this.data.length
  }
}

function mergeKLists(lists: Array<ListNode | null>): ListNode | null {
  const ret = new ListNode(), q = new SmallHeap(lists)
  let p = ret
  
  while (q.size()) {
    p.next = q.pop()
    p = p.next
    p.next = null
  }
  return ret.next
}

leetCode 1508 子数组和排序后的区间和

这题也是用堆来解，重点是定义好节点的结构 type dataType = [val: number, pos: number]

第一个元素是原数组的每一项，第二项是原数组的累加位置

比如示例1的 [1, 2, 3, 4] 中的 1 的子数组有 [1] [1, 2] [1, 2, 3] [1, 2, 3, 4]

type dataType = [val: number, pos: number]
class Priority {
  private readonly data: dataType[]
  constructor() {
    this.data = []
  }
  
  size() {
    return this.data.length
  }
  
  push(val: dataType) {
    this.data.push(val)
    this.sortUp(this.data.length - 1)
  }
  
  pop() {
    if (!this.data.length) return null
    if (this.data.length === 1) return this.data.pop()
    const ret = this.data[0]
    this.data[0] = this.data.pop() as dataType
    this.sortDown(0)
    return ret
  }
  
  sortUp(i: number) {
    let parentIndex: number
    while (i) {
      parentIndex = (i - 1) >> 1
      if (this.data[i][0] < this.data[parentIndex][0]) this.swap(i, parentIndex)
      else return
      i = parentIndex
    }
  }
  
  sortDown(i: number) {
    let target: number, lChild: number, rChild: number
    while (i < this.data.length) {
      target = i, lChild = (i << 1) + 1, rChild = (i << 1) + 2
      if (lChild < this.data.length && this.data[lChild][0] < this.data[target][0]) target = lChild
      if (rChild < this.data.length && this.data[rChild][0] < this.data[target][0]) target = rChild
      if (i === target) return
      this.swap(i, target)
      i = target
    }
  }
  
  swap(i: number, j: number) {
    [this.data[i], this.data[j]] = [this.data[j], this.data[i]]
  }
}
function rangeSum(nums: number[], n: number, left: number, right: number): number {
  let ans = 0, item: dataType
  const q = new Priority(), mod = 1e9 + 7
  //* 初始化
  nums.forEach((num, i) => q.push([num, i]))
  //* 获取升序数组
  for (let i = 1; i <= right && q.size(); i++) {
    item = q.pop() as dataType
    if (item[1] + 1 < nums.length) q.push([item[0] + nums[item[1] + 1], item[1] + 1])
    if (i >= left) ans = (item[0] + ans) % mod
  }
  return ans
}

面试题 04.08 首个共同祖先

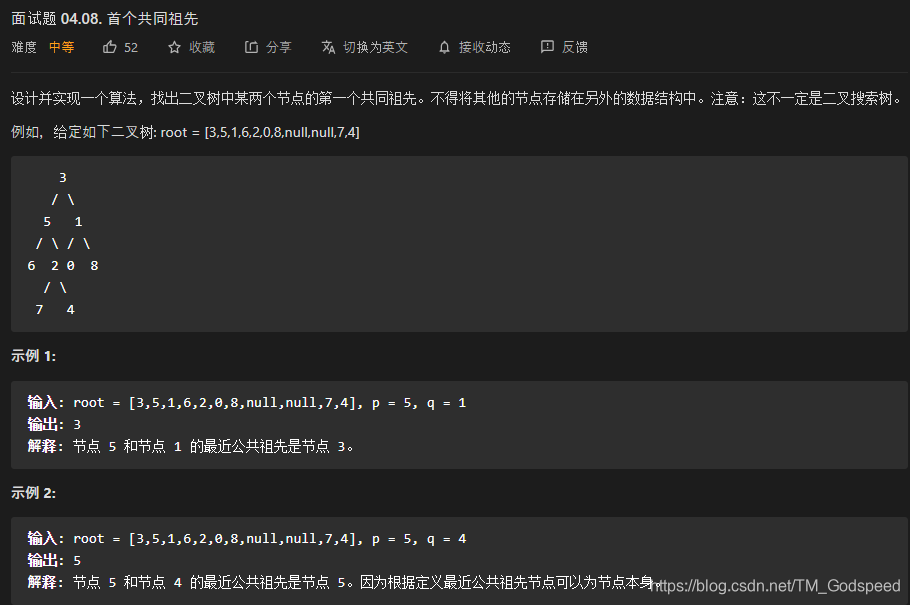
首先定义一个递归函数，赋予它的意义是找到子树中的目标节点

如果在左右子树都找到目标节点，就说明本节点是目标节点的共同祖先；
如果左树是空，则说明首个共同祖先在右树；
否则，首个共同祖先在左树。

//@ts-nocheck
/**
 * Definition for a binary tree node.
 * function TreeNode(val) {
 *     this.val = val;
 *     this.left = this.right = null;
 * }
 */
/**
 * @param {TreeNode} root
 * @param {TreeNode} p
 * @param {TreeNode} q
 * @return {TreeNode}
 */
var lowestCommonAncestor = function(root, p, q) {
  if (!root) return null
  if (root === p || root === q) return root
  const lTree = lowestCommonAncestor(root.left, p, q), rTree = lowestCommonAncestor(root.right, p, q)
  if (lTree && rTree) return root
  if (!rTree && lTree) return lTree
  return rTree
}

1302 层数最深叶子节点的和

这题使用递归，接收节点、深度和状态记录

状态记录 type stateType = [val: number, depth: number] 第一个参数是累加和，第二个参数记录的是最深层数

type stateType = [val: number, depth: number]
function counter(root: TreeNode | null, depth: number, curState: stateType) {
  if (!root) return curState
  if (depth === curState[1]) {
    curState[0] += root.val
  } else if (depth > curState[1]) {
    curState[0] = root.val
    curState[1] = depth
  }
  
  counter(root.left, depth + 1, curState)
  counter(root.right, depth + 1, curState)
}

function deepestLeavesSum(root: TreeNode | null): number {
  if (!root) return 0
  const curState: stateType = [root.val, 0]
  counter(root, 0, curState)
  return curState[0]
}

发发牢骚

工作之后时间真的少很多，一周加班三四天，晚上回到家锻炼洗漱后就差不多该睡觉了。。有时题目虽然在公司偷偷摸鱼做完，但是不方便写，忙了一天回到家后真的是精疲力竭，挺无语的

本来还在学校的时候想着毕业后自己一个人生活了就不会被干扰、就有更多时间钻研了，但是事实是每个时间段都有那个时间段的烦恼，唉，想办法克服当下困难才是正道。。继续加油吧，总会有上岸的一天的