[数据结构与算法] 支持向量机理论推导

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 支持向量机理论推导 -> 正文阅读

[数据结构与算法]支持向量机理论推导

在这里插入图片描述

关于松弛变量的解释在文章末尾。在这里插入图片描述

所有特征值都是非负数的矩阵被称为半正定（positive semidefinite）。
在这里插入图片描述

。。。。。。。。
在这里插入图片描述

。。。。。。
在这里插入图片描述

①松弛变量：

引入松弛因子的两点考虑：存在偏离总体样本的样本点使得求得的超平面并非最优超平面；存在严重偏离总体样本的样本点使得样本结构线性不可分。

松弛变量的引入便于在更大的可行域内求解，对应数据点? $x_{i}$ ?允许偏移 functional margin 的量。

使用松弛变量处理 outliers 方法：
????????假定数据线性可分，即可以找到一个可行的超平面将数据分开。处理非线性数据时，虽然可以将数据映射到高维空间，使线性分隔的概率增加，但对于某些情况还是很难处理。

????????例如并非因为数据本身是非线性结构的，只是因为数据有噪音。对于偏离正常位置很远的数据点，称之为 outlier 。outlier 的存在有可能造成很大的影响，因为超平面本身就是只有少数几个 support vector 组成的，如果 support vector 里又存在 outlier 的话，其影响就很大。例如下图：

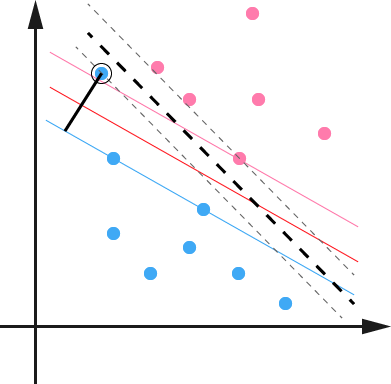
????????黑圈圈起来的蓝点是 outlier ，它偏离了原本所应该在的空间，如果忽略掉它的话，原来的分隔超平面较好，但由于 outlier 的出现，导致分隔超平面被挤歪，变成黑色虚线，同时 margin 也相应变小。如果这个 outlier 再往右上移动一些距离的话，将无法构造出能将数据分开的超平面来。

????????为了处理该情况，SVM 允许数据点在一定程度上偏离超平面。例如上图，黑色实线所对应的距离，就是该 outlier 偏离的距离，如果把它移动回来，就刚好落在原来的超平面蓝色间隔边界上，而不会使得超平面发生变形了。

????????考虑到outlier问题，约束条件将变成：

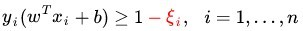
????????其中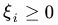称为松弛变量 (slack variable) ，对应数据点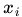允许偏离的 functional margin 的量。如果运行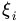任意大的话，那任意的超平面都符合条件。所以，在原来的目标函数后面加上一项，使得这些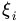的总和也要最小：

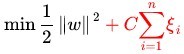
②拉格朗日乘数法

???????求? $z=f\left ( x,y \right )$ ?在条件? $\varphi \left ( x,y \right )=0$ ?的条件极值的一般方法为：

???????（1）构造拉格朗日函数? $F(x,y,\lambda )=f(x,y)+\lambda \varphi (x,y)$ ?；

???????（2）将 $F(x,y,\lambda )$ ?分别对? $x,y,\lambda$ ?求偏导数，构造方程组?

$\left\{\begin{matrix} {f}'_{x}(x,y)+\lambda {\varphi }'_{x}(x,y)=0 & \\ {f}'_{y}(x,y)+\lambda {\varphi }'_{y}(x,y)=0 & \\ \varphi (x,y)=0 & \end{matrix}\right.$

???????解出? $x,y,\lambda$ ，则其中? $(x,y)$ ?就是函数? $f(x,y)$ ?在条件 $\varphi (x,y)=0$ ?下的可能的极值点。

???????以上方法可推广到至于? $n$ ?元函数在? $m$ ?个约束条件下的极值问题，如求? $u=f(x,y,z)$ ?在条件? $\varphi (x,y,z)=0,\psi (x,y,z)=0$ ?下的极值，可构造拉格朗日函数? $F(x,y,z,\lambda ,\mu )=f+\lambda \varphi +\mu \psi$ .

? ? ? ?将? $F$ ?对? $x,y,z,\lambda ,\mu$ ?分别求偏导数，并构造方程组

? ? ? ? $\left\{\begin{matrix} {f}'_{x}(x,y,z)+\lambda {\varphi }'_{x}(x,y,z)+\mu {\psi }'_{x}(x,y,z)=0\\ {f}'_{y}(x,y,z)+\lambda {\varphi }'_{y}(x,y,z)+\mu {\psi }'_{y}(x,y,z)=0\\ {f}'_{z}(x,y,z)+\lambda {\varphi }'_{z}(x,y,z)+\mu {\psi }'_{z}(x,y,z)=0\\ \varphi (x,y,z)=0\\ \psi (x,y,z)=0 \end{matrix}\right.$