[数据结构与算法]5.10.如何调度考生的座位

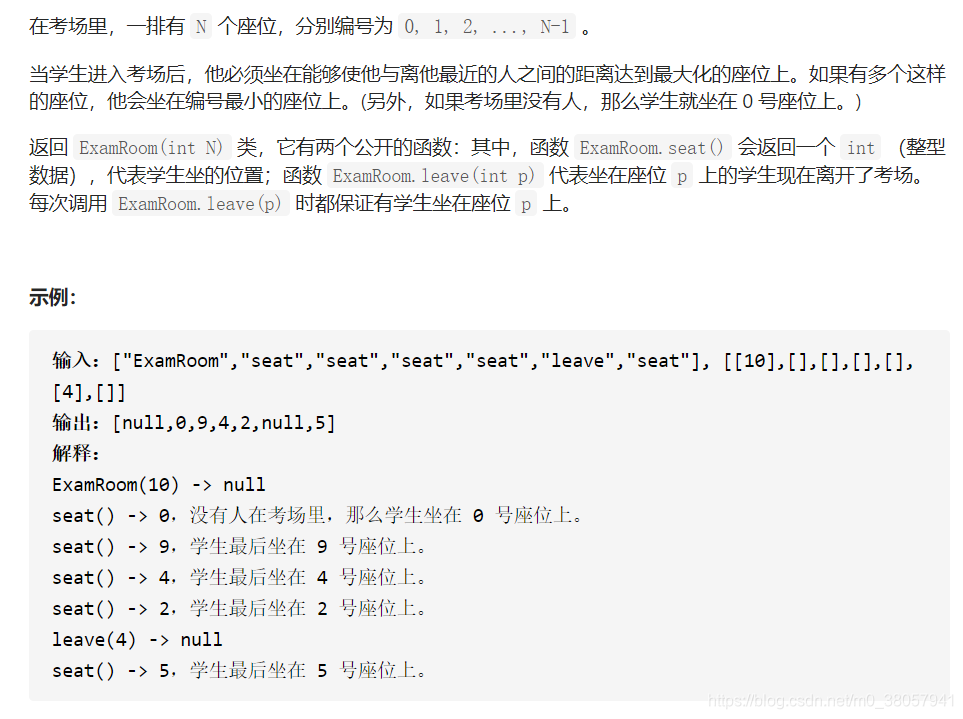
855. 考场就座

1.题目分析——线段切分法
遇到动态过程中取最值的问题，肯定是要使用有序数组，常用的数据结构就是二叉堆、平衡二叉搜索树。

• 1.本问题就是寻找某两个学生p、q为端点的线段，找出最长的线段，从中间切分开；
• 2.建立TreeSet<int []>数据结构，存储这样的线段,按线段长度升序排列，长度相同则按左侧索引降序；int[]是一个含有两个元素的数组，分别是线段的左、右端点p、q；
• 3.建立Map<Integer,int[]> startMap、Map<Integer,int[]> endMap;数据结构存储以坐标x为起始的线段、以坐标x为结尾的线段；

2.代码

class ExamRoom {

    将端点p映射到以p为 左端点的线段
    private Map<Integer,int[]> startMap;

    将端点p映射到以p为 右端点的线段
    private Map<Integer,int[]> endMap;

    根据线段长度从小到大存放所有线段
    private TreeSet<int[]> pq;

    表示最N个座位： 0 ~ N-1
    private int N;

    public ExamRoom(int n) {
        this.N = n;
        startMap = new HashMap<>();
        endMap = new HashMap<>();
        
        新建有序集合
        pq = new TreeSet<>(
                (a,b) -> {
                    算出两个线段的长度
                    int distA = distance(a);
                    int distB = distance(b);
                    
                    长度相同，索引小在后边
                    if (distA == distB){
                        return b[0] - a[0];
                    }
                    return distA - distB;
                }
        );
        
        在有序集合中先放一个虚拟线段
        addInterval(new int[]{-1, this.N});
    }
    
    删除线段
    private void removeInterval(int[] intv){
        pq.remove(intv);
        startMap.remove(intv[0]);
        endMap.remove(intv[1]);
    }
    
    增加线段
    private void addInterval(int[] intv){
        pq.add(intv);
        startMap.put(intv[0], intv);
        endMap.put(intv[1], intv);
    }
    
    计算线段的长度
    private int distance(int[] intv){
        int x = intv[0];
        int y = intv[1];
        if (x == -1) return y;
        if (y == N) return N-1-x;
        
        中点和端点的长度
        return (y-x) / 2;
    }

    public int seat() {
        
        从有序集合中拿出最长的线段
        int[] longest = pq.last();
        int x = longest[0];
        int y = longest[1];
        int seat;
        
        if (x==-1){
            情况1：最左边没人 肯定坐在最左边
            seat = 0;
        } else if (y == N){
            情况2：最右边没人 坐在最右边
            seat = N - 1;
        } else {
            情况3：不是边界，就坐在中间  防溢出写法
            seat = (y - x)/2 + x;
        }
        
         将最长的线段划分为2段
        int[] left = new int[]{x,seat};
        int[] right = new int[]{seat,y};
        
        移除最长的
        removeInterval(longest);
        添加进左右两个最新的
        addInterval(left);
        addInterval(right);
        
        return seat;
    }

    public void leave(int p) {
        将p左右的线段找出来
        int[] right = startMap.get(p);
        int[] left = endMap.get(p);
        
        将两条线段合为一条
        int[] merged = new int[]{left[0],right[1]};
        
        删除旧线段
        removeInterval(left);
        removeInterval(right);
        
        添加新线段
        addInterval(merged);
    }
}

/**
 * Your ExamRoom object will be instantiated and called as such:
 * ExamRoom obj = new ExamRoom(n);
 * int param_1 = obj.seat();
 * obj.leave(p);
 */