[数据结构与算法]图的遍历：深度优先遍历(DFS)

深度优先遍历(Depth First Search)

深度优先遍历类似于树的先序遍历

1.深度优先搜索遍历连通图

在无向图中任意两个顶点都是连通的(可以不是直接相连)，则称该图为连通图

假设从顶点 $V_1$出发，访问序列为
$$V_1\to V_2\to V_3\to V_4\to V_3(已访问)\to V_5$$

bool visited[MVNum];	//标记顶点是否被访问过，其初值为"false"
void DFS(Graph G, int n){	//传入有n个顶点的连通图G
	cout << v;	//输出图中某个顶点在数组中的下标
	visited[v]=true;	//访问第v个顶点，并置访问标志数组相应值为true
	for(w=FirstAdjVex(G,v); w>=0; w=NextAdjVex(G,v,w))	//这里的FirstAdjVex和NextAdjVex没有具体展开。如果图的存储结构不同，这两个的实现方法不同
	//依次检查v的所有邻接点w
	//FirstAdjVex(G,v)表示v的第一个邻接点
	//w>=0表示存在邻接点
	//NextAdjVex(G,v,w)表示v的相对于w的下一个邻接点
		if(!visited[w])
			DFS(G,w);	//对v的尚未访问的邻接顶点w递归调用DFS
}

2.深度优先搜索遍历非连通图

连通分量
下面两个图是上面非连通图的两个连通分量

每调用一次上面遍历连通图的算法，有多少次调用，就说明图中有多少个连通分量
（将非连通图分解为连通分量，分别进行遍历）

void DFSTraverse(Graph G){	//传入非连通图G
	for(v=0; v<G.vexnum; ++v)
		visited[v]=false;	//访问标志数组初始化
	for(v=0; v<G.vexnum; ++v)
		if(!visited[v]) 	//循环调用上面遍历连通图的算法DFS
			DFS(G,v);		//对未访问的顶点进行访问
}

3.深度优先搜索遍历以结构为邻接矩阵的图

无向图

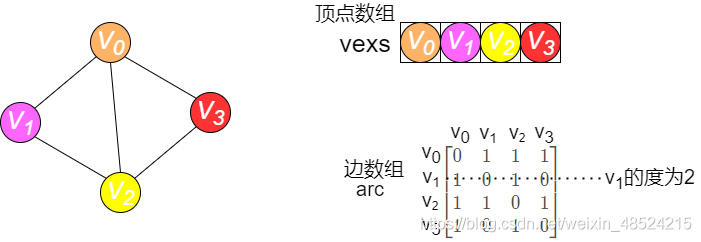
有向图

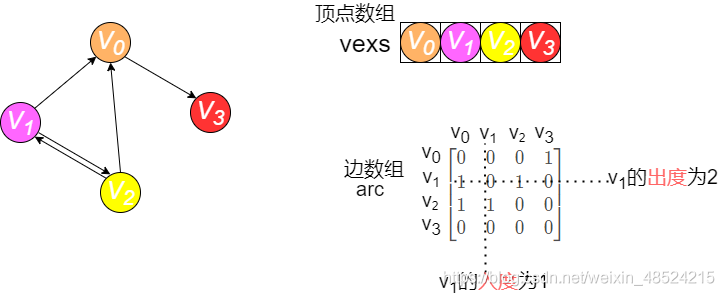
DFS只是对通道是否存在进行判断，对无向图和有向图算法上没有变化，完全通用

void DFS_AM(AMGraph G, int v){	//传入有向/无向图、第一个要访问的顶点在一维数组中的下标
	cout << v;	//输出某个顶点在一维数组中的下标
	visited[v]=true;	//访问第v个顶点，并置访问标志数组相应值为true
	for(w=0; w<G.vexnum; w++)	//依次检查邻接矩阵v所在行
		if((G.arcs[v][w] != 0) && (!visited[w]))
			DFS_AM(G,w);	//递归遍历未访问的顶点
}

4.深度优先搜索遍历以结构为邻接表的图

无向图

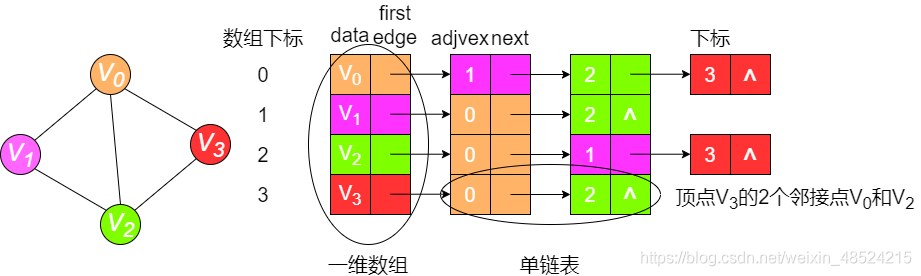
有向图

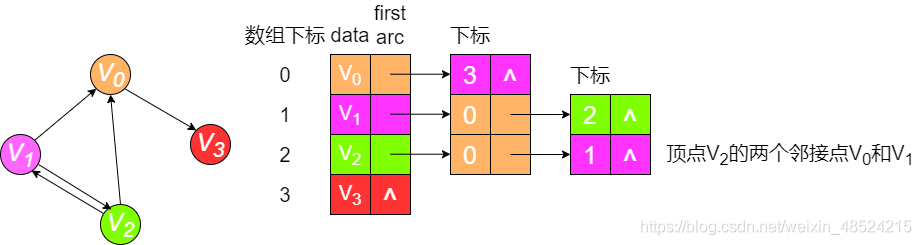
void DSL_AL(ALGraph G, int v){
	cout << v;	//输出某个顶点在一维数组中的下标
	visited[v]=true;	//访问第v个顶点，并置访问标志数组相应值为true
	p=G.vertices[v].firstarc;	//将下标为v的顶点的第一邻接点指针域命名为p
	while(p != NULL){	//下标为v的顶点的第一邻接点非空
		w=p->adjvex;	//p所指结点的数据域，该数据域是顶点在一维数组中的下标，将该下标赋值给w
		if(!visited[w])	//下标为w的顶点未访问过
			DSL_AL(G,w);	//递归遍历
		p=p->nextarc;	//现在用p指向p->nextarc所指的结点,以便下一次遍历时使用p
	}
}