一、树
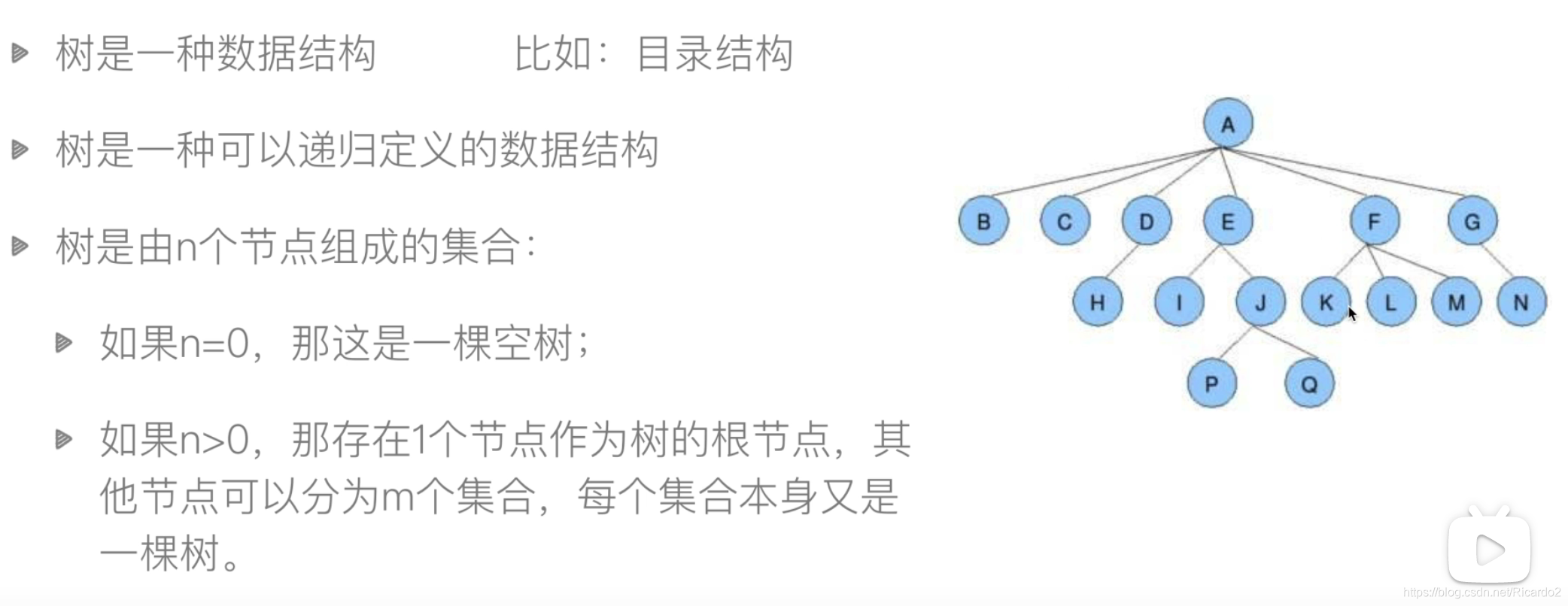
1、模拟文件系统
class Node:
def __init__(self, name, type='dir'):
self.name = name
self.type = type # "dir" or "file"
self.children = []
self.parent = None
def __repr__(self):
return self.name
class FileSystemTree:
def __init__(self):
self.root = Node("/")
self.now = self.root
def mkdir(self, name): # 创建目录
if name[-1] != "/":
name += "/"
node = Node(name)
self.now.children.append(node)
node.parent = self.now
def ls(self): # 返回子目录
return self.now.children
def cd(self, name): # 切换到name目录
if name[-1] != "/":
name += "/"
if name == "../": # 向上切换到parent
self.now = self.now.parent
return
for child in self.now.children: # 向下切换
if child.name == name:
self.now = child
return
else:
raise ValueError("invalid dir")
tree = FileSystemTree()
tree.mkdir("var/")
tree.mkdir("bin/")
tree.mkdir("usr/")
print(tree.now) # 输出”\“
print(tree.now.children) # 输出[var/, bin/, usr/]
tree.cd("bin/")
print(tree.now) # 输出 bin\
tree.cd("../")
print(tree.now) # 输出”\“
二、二叉树
度不超过2的树。
二叉树的链式存储:将二叉树的节点定义为一个对象,节点之间通过类似链表的链接方式来连接。
class BiTreeNode:
def __init__(self,data):
self.data=data
self.lchild=None #左孩子
self.rchild=None #右孩子
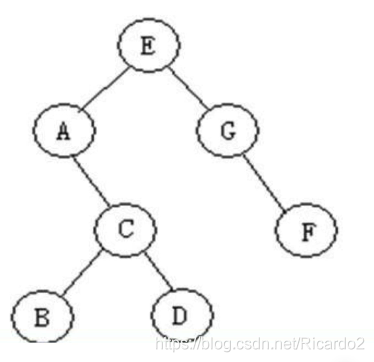
1、二叉树的遍历
前序遍历:EACBDGF
中序遍历:ABCDEGF
后序遍历:BDCAFGE
层次遍历:EAGCFBD
class BiTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None # 左孩子
self.rchild = None # 右孩子
a = BiTreeNode("A")
b = BiTreeNode("B")
c = BiTreeNode("C")
d = BiTreeNode("D")
e = BiTreeNode("E")
f = BiTreeNode("F")
g = BiTreeNode("G")
e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f
root = e
def pre_order(root): # 前序遍历[E[A[C[BD]]][G[F]]
if root:
print(root.data, end=',')
pre_order(root.lchild)
pre_order(root.rchild)
def in_order(root): # 中序遍历[A[BCD]]E[GF]
if root:
in_order(root.lchild)
print(root.data, end=',')
in_order(root.rchild)
def post_order(root): # 后序遍历
if root:
post_order(root.lchild)
post_order(root.rchild)
print(root.data, end=',')
from collections import deque
def level_order(root): # 层次遍历
queue = deque()
queue.append(root)
while len(queue) > 0:
node = queue.popleft()
print(node.data, end=',')
if node.lchild:
queue.append(node.lchild)
if node.rchild:
queue.append(node.rchild)
2、二叉搜索树
二叉搜索树是一颗二叉树且满足性质:设x是二叉树的一个节点,如果y是x左子树的一个节点,那么y.key≤x.key;如果y是x右子树的一个节点,那么y.key≤≥.key。
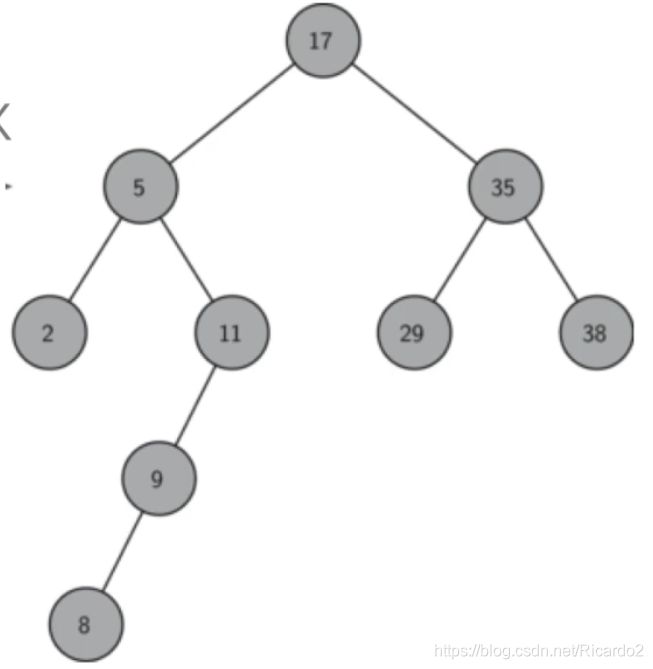
2.1二叉搜索树的插入、搜索、删除
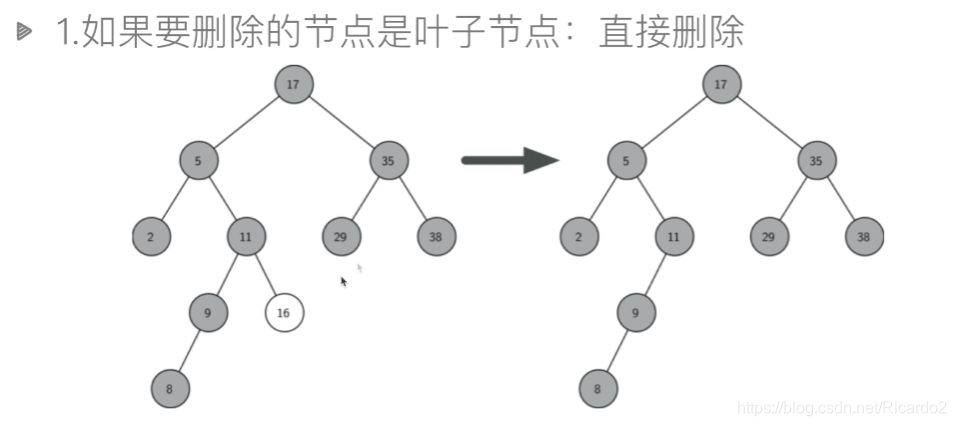
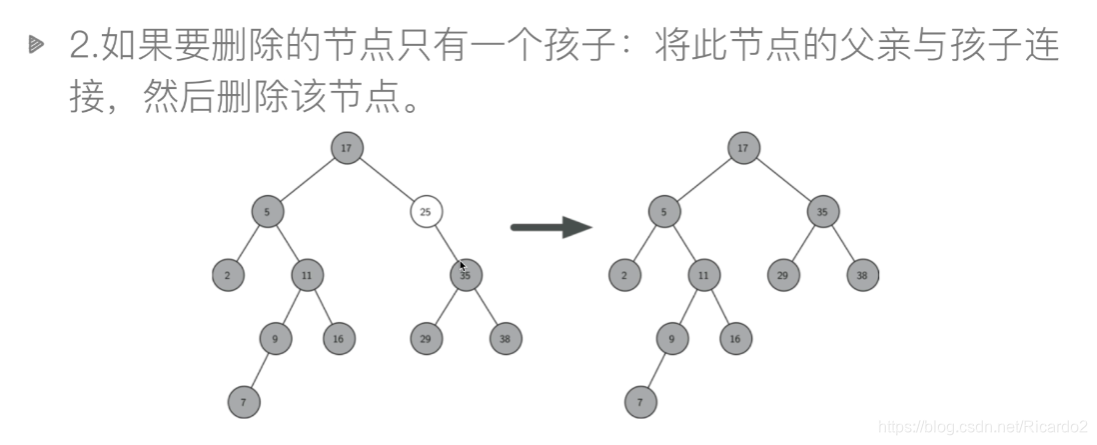
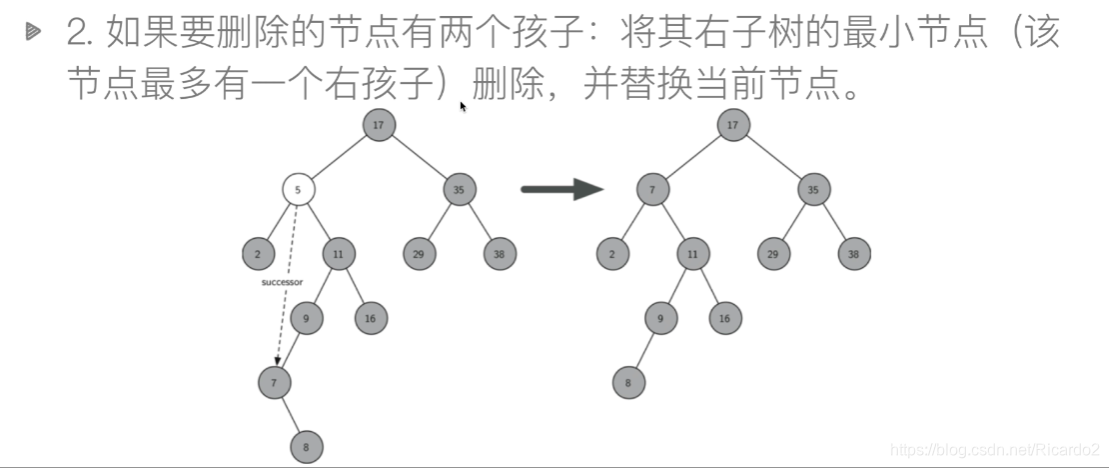
class BiTreeNode:
def __init__(self, data):
self.data = data
self.lchild = None # 左孩子
self.rchild = None # 右孩子
self.parent = None
class BST:
def __init__(self, li=None):
self.root = None
if li:
# 将列表中的元素按二叉搜索树插入
for val in li:
self.insert(val)
def insert(self, val):
# 插入
p = self.root
if not p:
self.root = BiTreeNode(val)
return
while True:
if val < p.data:
if p.lchild:
p = p.lchild
else:
p.lchild = BiTreeNode(val)
p.lchild.parent = p
return
elif val > p.data:
if p.rchild:
p = p.rchild
else:
p.rchild = BiTreeNode(val)
p.rchild.parent = p
return
else:
return
def query(self, val):
# 查找
p = self.root
while p:
if p.data < val:
p = p.rchild
elif p.data > val:
p = p.lchild
else:
return p
return None
def remove_node_1(self, node):
# 情况1:node是叶子节点
if not node.parent: # node为根节点
self.root = None
if node == node.parent.lchild: # node是它父亲的左孩子
node.parent.lchild = None
else: # node是它父亲的右孩子
node.parent.rchild = None
def remove_node_2_1(self, node):
# 情况2_1:node只有一个左孩子
if not node.parent: # 根节点
self.root = node.lchild
node.lchild.parent = None
elif node == node.parent.lchild:
node.parent.lchild = node.lchild
node.lchild.parent = node.parent
else:
node.parent.rchild = node.lchild
node.lchild.parent = node.parent
def remove_node_2_2(self, node):
# 情况2_2:node只有一个右孩子
if not node.parent:
self.root = node.rchild
elif node == node.parent.lchild:
node.parent.lchild = node.rchild
node.rchild.parent = node.parent
else:
node.parent.rchild = node.rchild
node.rchild.parent = node.parent
def delete(self, val):
if self.root: # 不是空树
node = self.query(val)
if not node: # node不存在
return False
if not node.lchild and not node.rchild: # 情况1
self.remove_node_1(node)
elif not node.rchild: # 情况2_1
self.remove_node_2_1(node)
elif not node.lchild: # 情况2_2
self.remove_node_2_2(node)
else: # 情况3:两个孩子都有
min_node = node.lchild
while min_node.lchild:
min_node = min_node.lchild
node.data = min_node.data
# 删除min_node(为叶子节点或者只有一个右孩子)
if min_node.rchild:
self.remove_node_2_2(min_node)
else:
self.remove_node_1(min_node)
def in_order(self, root): # 中序遍历
if root:
self.in_order(root.lchild)
print(root.data, end=',')
self.in_order(root.rchild)
def pre_order(self, root): # 前序遍历
if root:
print(root.data, end=',')
self.pre_order(root.lchild)
self.pre_order(root.rchild)
tree = BST([5, 17, 35, 2, 11, 29, 38, 9, 8])
tree.in_order(tree.root) # 对于二叉搜索树,其中序遍历输出结果是升序排列
print("")
tree.pre_order(tree.root)
print("")
print(tree.query(2).data) # 搜索
tree.delete(4)
tree.in_order(tree.root)
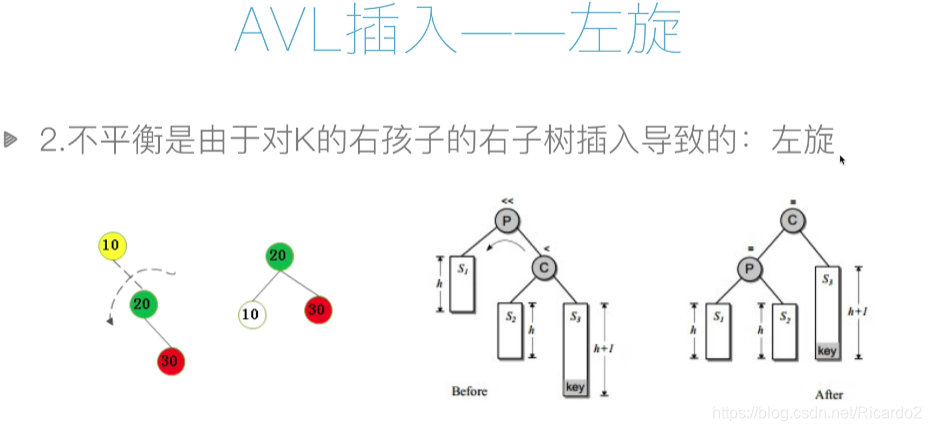
3、AVL树
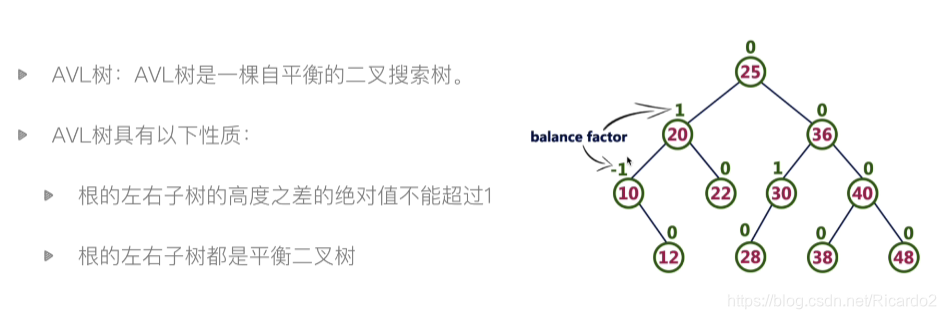

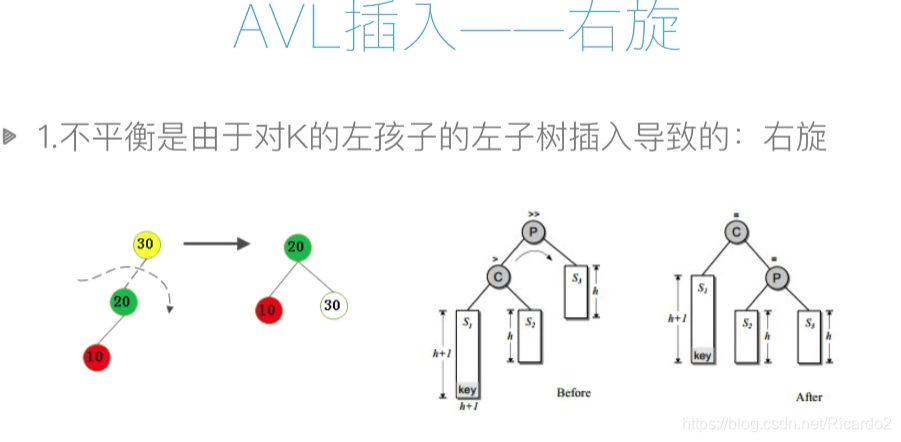
from bst import BiTreeNode, BST #将2.1处的代码存为bst.py,此处调用
class AVLNode(BiTreeNode):
def __init__(self, data):
BiTreeNode.__init__(self, data)
self.bf = 0
class AVLTree(BST):
def __init__(self, li=None):
BST.__init__(self, li)
def rotate_left(self, p, c): # 左旋
s2 = c.lchild
p.rchild = s2
if s2:
s2.parent = p
c.lchild = p
p.parent = c
p.bf = 0
c.bf = 0
return c
def rotate_right(self, p, c): # 右旋
s2 = c.rchild
p.lchild = s2
if s2:
s2.parent = p
c.rchild = p
p.parent = c
p.bf = 0
c.bf = 0
return c
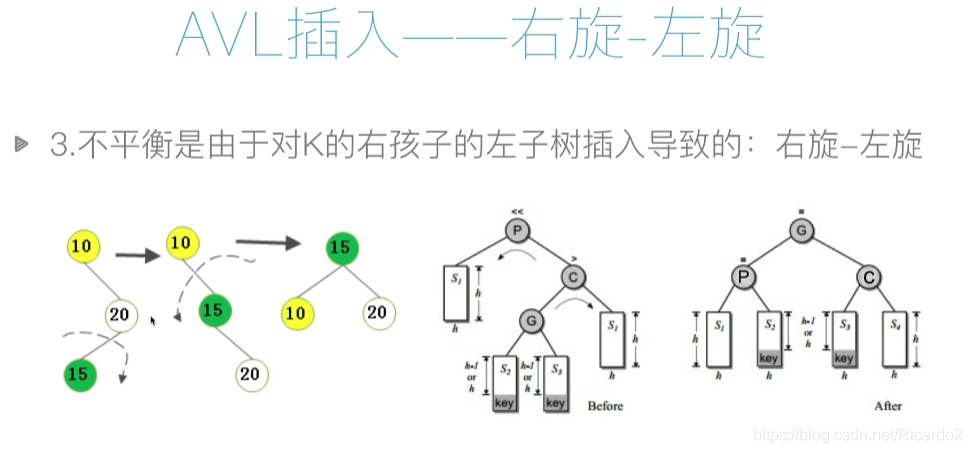
def rotate_right_left(self, p, c): # 右旋——左旋
g = c.lchild
s3 = g.rchild
c.lchild = s3
if s3:
s3.parent = c
g.rchild = c
c.parent = g
s2 = g.lchild
p.rchild = s2
if s2:
s2.parent = p
g.lchild = p
p.parent = g
# 更新bf
if g.bf > 0: # g.bf==1
p.bf = -1
c.bf = 0
else: # g.bf==-1
p.bf = 0
c.bf = 1
g.bf = 0
return g
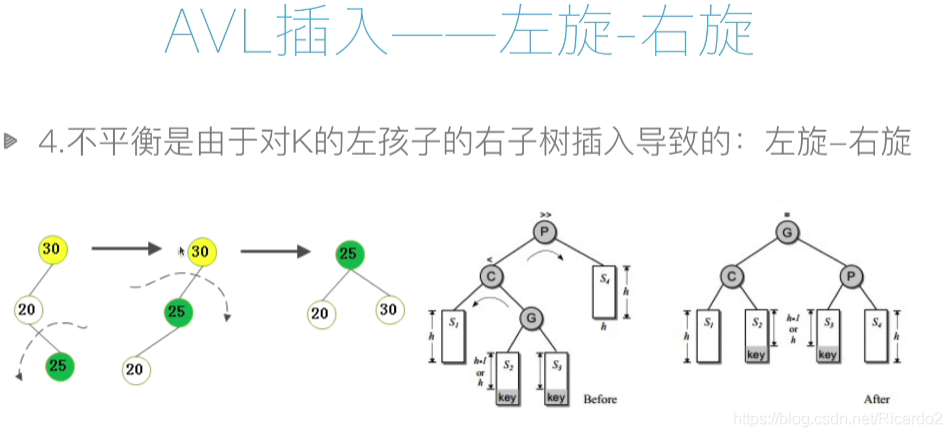
def rotate_left_right(self, p, c): # 左旋——右旋
g = c.rchild
s2 = g.lchild
c.rchild = s2
if s2:
s2.parent = c
g.lchild = c
c.parent = g
s3 = g.rchild
p.lchild = s3
if s3:
s3.parent = p
g.rchild = p
p.parent = g
# 更新bf
if g.bf < 0:
p.bf = 1
c.bf = 0
else:
p.bf = 0
c.bf = -1
g.bf = 0
return g
def insert(self, val):
# 1、做插入
p = self.root
if not p:
self.root = AVLNode(val)
return
while True:
if val < p.data:
if p.lchild:
p = p.lchild
node = p.lchild # node存储的是插入的节点
else:
p.lchild = AVLNode(val)
p.lchild.parent = p
node = p.lchild # node存储的是插入的节点
break
elif val > p.data:
if p.rchild:
p = p.rchild
else:
p.rchild = AVLNode(val)
p.rchild.parent = p
node = p.rchild
break
else:
return
# 2、更新bf参数
while node.parent: # node.parent不空
if node.parent.lchild == node: # 传递是从左子树来的,更新后的node.parent的bf-=1
if node.parent.bf < 0: # 原来的node。parent。bf==-1,更新后变成-2
# 做旋转
g = node.parent.parent # 用于连接旋转之后的子树
x = node.parent # 旋转之前的子树的根
if node.bf > 0:
n = self.rotate_left_right(node.parent, node)
else:
n = self.rotate_right(node.parent, node)
elif node.parent.bf > 0: # 原来的node.parent.bf=1,更新之后变成0
node.parent.bf = 0
break
else: # 原来的node.parent.bf=0,更新之后变成-1
node.parent.bf = -1
node = node.parent
continue
else: # 传递是从右子树来的,更新后的node.parent的bf+=1
if node.parent.bf > 0: # 原来的node。parent。bf==1,更新后变成2
# 做旋转
g = node.parent.parent
x = node.parent
if node.bf < 0:
n = self.rotate_right_left(node.parent, node)
else:
n = self.rotate_left(node.parent, node)
elif node.parent.bf < 0: # 原来的node。parent。bf==-1,更新后变成0
node.parent.bf = 0
break
else: # 原来的node.parent.bf=0,更新之后变成1
node.parent.bf = 1
node.parent = node
continue
# 连接旋转之后的子树
n.parent = g
if g:
if x == g.lchild:
g.lchild = n
else:
g.rchild = n
break
else:
self.root = n
break
tree = AVLTree([9, 8, 7, 6, 5, 4, 3, 2, 1])
tree.pre_order(tree.root)
print("")
tree.in_order(tree.root)