开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> AVL树原理详解与实现（附代码） -> 正文阅读

[数据结构与算法]AVL树原理详解与实现（附代码）

上一篇文章讲了二叉搜索树，但是它会在极端情况下退化为链表，造成查找时间复杂度退化为 $O (N)$ ，那么怎样才能让它不退化为链表呢？这篇文章告诉你，快来看看把！

1. 平衡二叉树的定义

平衡说的是树的高度平衡，平衡二叉树可以这么定义：

一颗空树
如果不是空树，那么它的左子树和右子树都是平衡二叉树，且左右子树的高度差绝对值不超过1

树的高度怎么定义？

如果是空树，高度为0
如果不是空树，那高度就是左子树和右子树的高度最大值+1；

举个例子：

在这里插入图片描述
A的左子树高度3，右子树高度为1，左右子树高度差2，因此这不是平衡二叉树

又如：
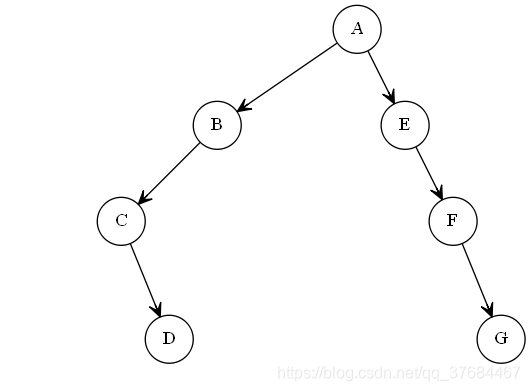
在这里插入图片描述
虽然A的左子树和右子树的高度差是0，但是其左右子树都不是平衡二叉树，因此整棵树不平衡。

2. AVL树的调整

AVL树是一颗平衡的二叉搜索树，它与普通的二叉搜索树最大的区别就是它的平衡性，平衡性保证了二叉搜索树不会在某些情况下退化为链表，保证了最坏的查找时间复杂度为 $O (N)$ ，那么，AVL树如何保证平衡的呢？就是通过调整。那AVL树不平衡的时候，有哪些情况呢？下面一个一个看。

案例1： 如下图所示的二叉树
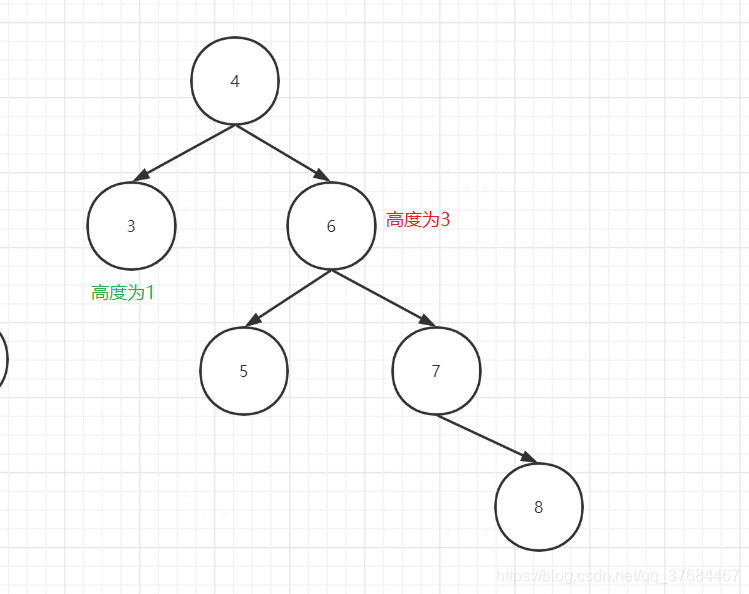
在这里插入图片描述

根节点1已经失去平衡了（左子树高度1，右子树高度3），现在我们需要做一个操作，使之平衡。这个操作不是只要保证这棵树再次平衡就可以了，还需要保证操作前后，树的中序遍历顺序不改变，就是说操作之后，整棵树还是一颗而二叉搜索树。因此我们要找到一个过程，它只调整数的结构，但不影响数的二叉搜索性质。
那如何操作呢？如下图所示：
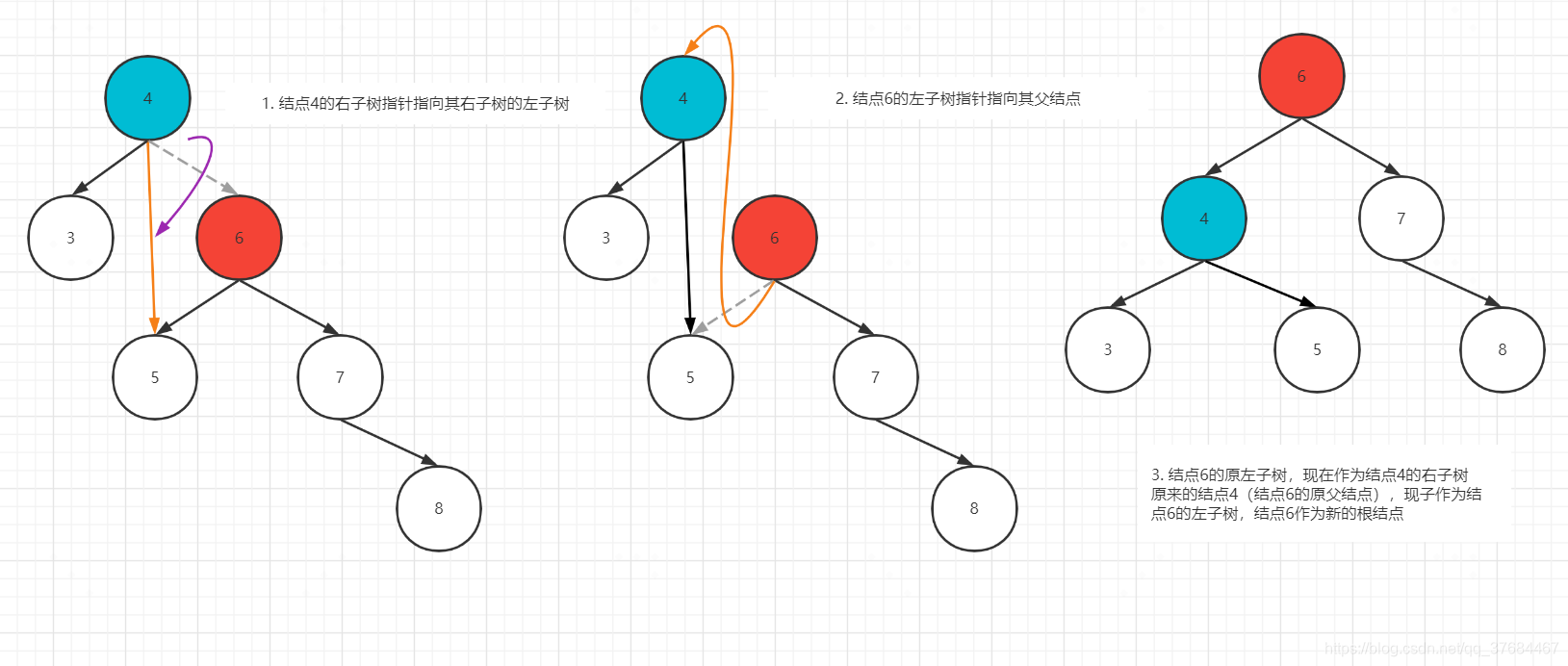
在这里插入图片描述
这样操作以后，整棵树是平衡的了，那还是二叉搜索树吗？我们只需要看看操作前后的中序遍历结果是不是一个有序列表即可。
操作之前中序遍历顺序：3，4，5，6，7，8
操作之后中序遍历顺序：3，4，5，6，7，8
可见这样的操作是可行的，我们不妨给这个操作起个名字，叫左旋。这样的蜜汁操作是怎么想到的呢？灵感一现吗？不，它是有依据的，如上图所示，根据BST的特性，

结点6的父节点4，以及4的左子树3，都是小于结点6的，因此可以整体放在结点6的左子树的位置；
而结点6的左子树5，比6小，但是至少比其父节点4要大，因此可以同时作为结点4的右子树。

案例2： 如下图所示的情况
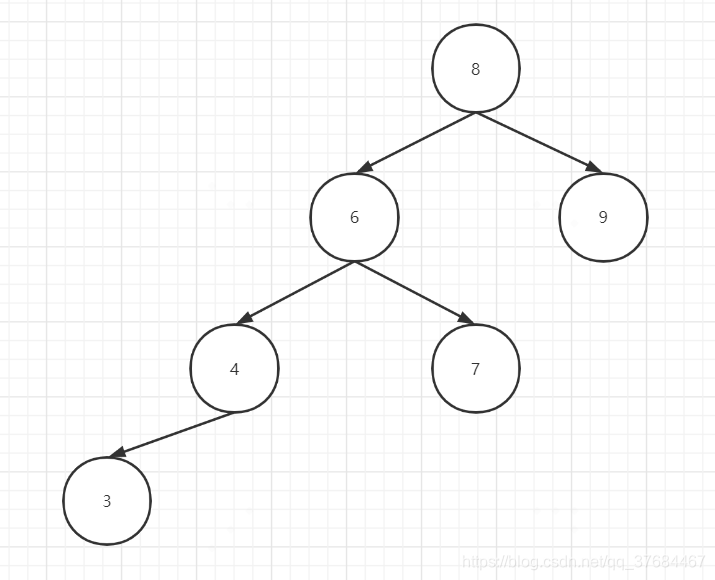
在这里插入图片描述
根结点8的左子树高度3，右子树高度1，这个情况其实跟上一个情况是对称的，调整这种情况的方式对应叫右旋，如下图所示：

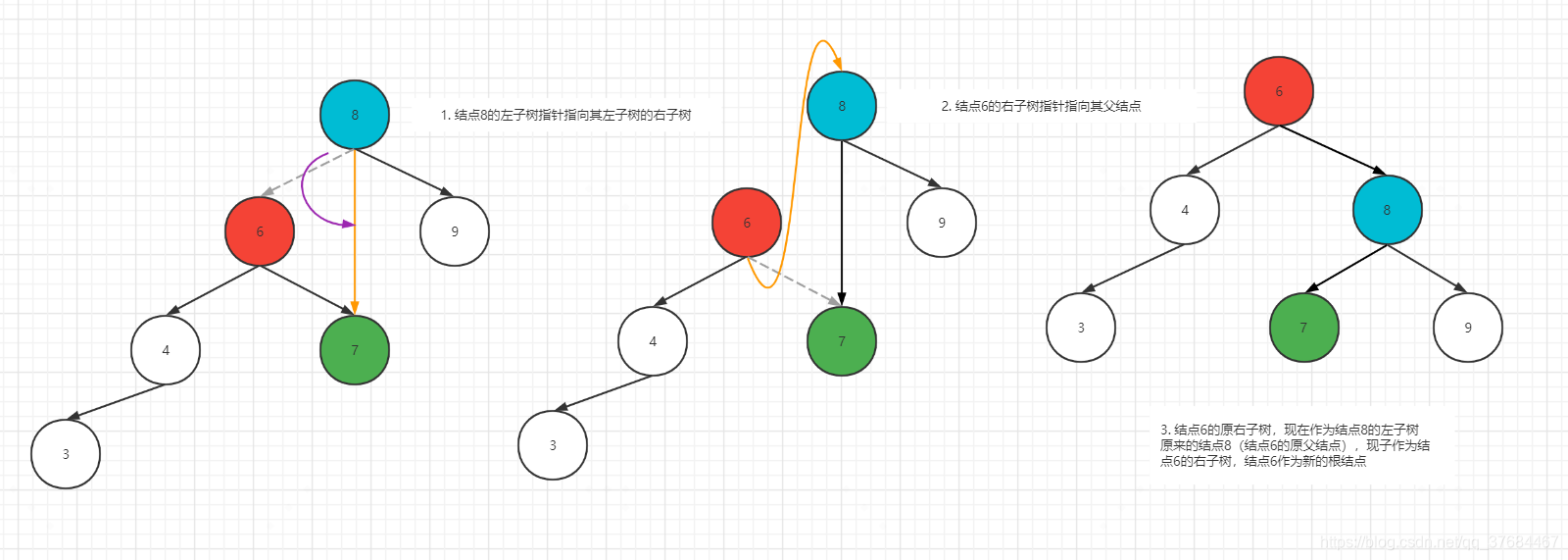
中序遍历结果这里就不验证了哈，原理与左旋类似。

案例3： 如下图所示的情况
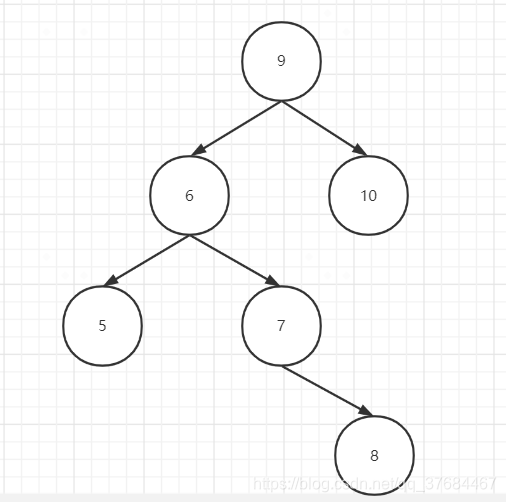
在这里插入图片描述
这个形状与案例2中的形状类似，结点9的左子树高度是3，右子树高度1，只不过结点9的左子树的左子树比结点9的左子树的右子树的高度低，如果我们可以把结点9的左子树进行一番操作，改成与案例2中一样的形状就可以按照案例2的情况处理了，因此我们可以先结点9的左子树左旋操作，
在这里插入图片描述然后再按照案例2的方法右旋即可。

案例4： 最后一种情况
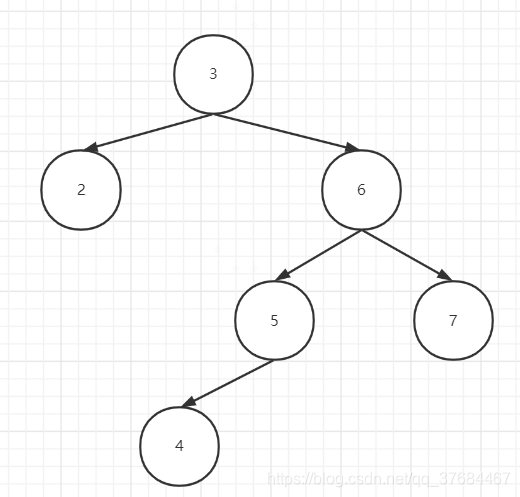
在这里插入图片描述
跟案例3类似，先对结点6右旋，再对结点3左旋即可。
我们对AVL树进行插入，删除以后，都需要检查树的平衡性，必要时，进行树的调整。

3. AVL树的实现

定义AVL树结点类

    class AVLNode<T extends Comparable<T>> {
        T data;
        AVLNode<T> left;
        AVLNode<T> right;
        int height; //树的高度

        public AVLNode(T data) {
            this.data = data;
            this.height = 1;//高度初始化为1
        }
    }

定义AVL树实现类

public class AVLTree<T extends Comparable<T>> {
    /**
     * 树的根节点
     */
    private AVLNode<T> rootNode;

    /**
     * AVL树的结点个数
     */
    private int size;
	
	//返回树的结点个数
    public int size() {
        return size;
    }
	// ... 其他方法
}

首先实现一些utils方法，

获取树结点的高度：

/**
 * 获取某个结点的高度
 *
 * @param node 需要获取其高度的结点
 * @return AVL树某个结点的高度
 */
private int height(AVLNode<T> node) {
    //如果树为空，则返回0，否则返回其height字段的值
    return node == null ? 0 : node.height;
}

更新树结点的高度

/**
 * 更新某个AVL树结点的高度
 *
 * @param node 需要更新高度的AVL树结点
 */
private void updateHeight(AVLNode<T> node) {
    //某个结点的高度是其左子树和右子树的高度的最大值 +1
    if (node != null) node.height = Math.max(height(node.left), height(node.right)) + 1;
}

获取树某个结点的平衡因子

/**
 * 获取AVL树某个结点的平衡因子
 * 平衡因子是左子树的高度减去右子树的高度
 *
 * @param node 需要获取其平衡因子的结点
 * @return AVL树某个结点的平衡因子
 */
private int balanceFactor(AVLNode<T> node) {
    return node == null ? 0 : height(node.left) - height(node.right);
}

右旋操作

/**
 * 对AVL树的某个结点进行右旋操作
 * 右旋的逻辑是，node的左指针指向其左子树的右子树，其左子树的右指针指向node，返回node的左子树
 *
 * @param node 需要右旋的结点
 * @return 右旋操作以后的根节点
 */
private AVLNode<T> rightRotate(AVLNode<T> node) {
    AVLNode<T> left = node.left;
    node.left = left.right;
    left.right = node;
    updateHeight(node);//先更新node的高度，然后才可以更新left的高度
    updateHeight(left);
    return left;
}

左旋操作

/**
 * 对AVL树的某个结点进行左旋操作
 * 左旋的逻辑是，node的右指针指向其右子树的左子树，其右子树的左指针指向node，返回node的右子树
 *
 * @param node 需要左旋的结点
 * @return 左旋操作以后的根节点
 */
private AVLNode<T> leftRotate(AVLNode<T> node) {
    AVLNode<T> right = node.right;
    node.right = right.left;
    right.left = node;
    updateHeight(node);
    updateHeight(right);
    return right;
}

调整树
当某棵树的平衡因子：

大于1，则代表需要右旋操作，如果此时其左子树的平衡因子小于0，则代表需要先左旋；
小于-1，则代表需要左旋操作，如果此时其右子树的平衡因子大于0，则代表需要先右旋。

根据这样的逻辑，调整某个结点的代码如下：

/**
 * 调整AVL树，主要是根据平衡因子进行旋转操作
 * 因为调整以后，可能改变树的根节点，因此调整方法返回新的根结点
 * 
 * @param root 待调整的根节点
 * @return 调整之后的根节点
 */
private AVLNode<T> adjustAVLTree(AVLNode<T> root) {
    if (root == null) return null;

    //判断是否平衡，如果平衡，则直接返回根节点
    int balanceFactor = balanceFactor(root);
    if (Math.abs(balanceFactor) <= 1) return root;

    //否则根据各种不平衡的情况，采取左旋和右旋进行调整
    if (balanceFactor > 1) {//当平衡因子大于1时，需要右旋解决

        // 如果根的左子树的平衡因子小于0 则说明根的左子树 右重左轻 需要先对其左旋
        if (balanceFactor(root.left) < 0) root.left = leftRotate(root.left);
        root = rightRotate(root);
    } else {//当平衡因子小于-1时，需要左旋解决

        // 如果根的右子树的平衡因子大于0 则说明根的右子树 左重右轻 需要先对其右旋
        if (balanceFactor(root.right) > 0) root.right = rightRotate(root.right);
        root = leftRotate(root);
    }
    return root;
}

找到某棵树最左的结点

/**
 * 找到AVL树某个结点上最左的结点
 *
 * @param root 需要搜索到的树根节点
 * @return root上最左的结点
 */
private AVLNode<T> mostLeft(AVLNode<T> root) {
    if (root == null) return null;
    AVLNode<T> cur = root;
    //只要cur的left不为空，则说明cur还有左子树，cur就不是最左的位置
    for (; cur.left != null; cur = cur.left) ;
    return cur;
}

put，remove，find方法实现：

put方法
与二叉搜索树插入类似，只不过这里需要树的调整：

/**
 * 添加元素到AVL树，不允许null 和重复元素
 *
 * @param value 待添加的元素
 * @return 添加成功--true，否则--false
 */
public boolean put(T value) {
    if (value == null) return false;
    AVLNode<T> newRoot = put(this.rootNode, value);
    if (newRoot == null) return false;
    this.rootNode = newRoot;
    return true;
}

/**
 * 添加一个元素到AVL树，因为添加以后可能会改变树的根，所以返回添加后的新的根节点
 *
 * @param root  AVL树根节点
 * @param value 待添加的元素
 * @return 添加后的根结点
 */
private AVLNode<T> put(AVLNode<T> root, T value) {
    if (root == null) {
        ++this.size;
        return new AVLNode<>(value);
    }
    // 如果找到某个元素和value相等，则不添加，返回
    if (root.data.compareTo(value) == 0) return null;
    if (value.compareTo(root.data) < 0) {//value小于根结点的值，则添加到左子树上，否则添加到右子树上
        AVLNode<T> newLeft = put(root.left, value);
        if (newLeft == null) return null;
        root.left = newLeft;
    } else {
        AVLNode<T> newRight = put(root.right, value);
        if (newRight == null) return null;
        root.right = newRight;
    }
    //更新高度
    updateHeight(root);

    //调整AVL树
    return adjustAVLTree(root);
}

find方法
与二叉搜索树类似

/**
 * 查找AVL树中是存在结点value
 *
 * @param value 待查找的结点
 * @return 存在--true，不存在--false
 */
public boolean find(T value) {
    if (value == null || this.rootNode == null) return false;
    AVLNode<T> cur = this.rootNode;
    while (cur != null) {
        if (cur.data.compareTo(value) == 0) return true;
        if (value.compareTo(cur.data) < 0) cur = cur.left;
        else cur = cur.right;
    }
    return false;
}

remove方法
为了方便设计，定义了一个remove的返回值类型

/**
 * 删除结果类
 *
 * @param <T>
 */
private static class RemoveResult<T extends Comparable<T>> {
    boolean success; //当前删除是否成功
    AVLNode<T> retNode; // 删除成功后 返回的新的根结点

    public RemoveResult(boolean success, AVLNode<T> retNode) {
        this.success = success;
        this.retNode = retNode;
    }

    public RemoveResult(boolean success) {
        this(success, null);
    }
}

/**
 * 删除元素
 *
 * @param value 待删除的元素
 * @return 删除成功--true，否则--false
 */
public boolean remove(T value) {
    if (value == null || this.rootNode == null) return false;
    RemoveResult<T> removeResult = remove(this.rootNode, value);
    //删除成功才记录返回的新的根结点
    if (removeResult.success) this.rootNode = removeResult.retNode;
    return removeResult.success;
}

/**
 * 删除某棵AVL树上某个结点，因为删除可能会更换根结点，因此需要返回删除以后的根结点
 *
 * @param root  树根结点
 * @param value 待删除的值
 * @return 成功返回new RemoveResult<>(true,新的树根节点); 否则 new RemoveResult<>(false,null)
 */
private RemoveResult<T> remove(AVLNode<T> root, T value) {
    //如果根为空，则直接返回删除失败
    if (root == null) return new RemoveResult<>(false);

    //找到带删除的结点，删除逻辑和BST大致一样
    if (root.data.compareTo(value) == 0) {
        if (root.left == null || root.right == null) {
            --size;
            if (root.left == null) root = root.right;
            else root = root.left;
        } else {//当左右子树都不为空时，先从右子树找出最左的结点，作为新的根， 然后将其从右子树删除，
            AVLNode<T> leftMostOfRight = mostLeft(root.right);
            leftMostOfRight.right = remove(root.right, leftMostOfRight.data).retNode;
            leftMostOfRight.left = root.left;
            root = leftMostOfRight;
        }
        //如果当前结点不是要删除的，则根据大小关系，分别跳到左右子树 进行删除
    } else if (value.compareTo(root.data) < 0) {
        RemoveResult<T> removeLeft = remove(root.left, value);
        if (!removeLeft.success) return removeLeft;
        root.left = removeLeft.retNode;
    } else {
        RemoveResult<T> removeRight = remove(root.right, value);
        if (!removeRight.success) return removeRight;
        root.right = removeRight.retNode;
    }
    //最后需要调整高度和平衡性
    updateHeight(root);
    return new RemoveResult<>(true, adjustAVLTree(root));
}

4. 完整代码，带测试程序

package com.victory.common.data_structure;

import java.util.HashSet;
import java.util.Scanner;
import java.util.Set;

/**
 * 平衡二叉树 AVL树的实现
 */
public class AVLTree<T extends Comparable<T>> {

    /**
     * 树的根节点
     */
    private AVLNode<T> rootNode;

    /**
     * AVL树的结点个数
     */
    private int size;

    public int size() {
        return size;
    }

    /**
     * 添加元素到AVL树，不允许null 和重复元素
     *
     * @param value 待添加的元素
     * @return 添加成功--true，否则--false
     */
    public boolean put(T value) {
        if (value == null) return false;
        AVLNode<T> newRoot = put(this.rootNode, value);
        if (newRoot == null) return false;
        this.rootNode = newRoot;
        return true;
    }

    /**
     * 查找AVL树中是存在结点value
     *
     * @param value 待查找的结点
     * @return 存在--true，不存在--false
     */
    public boolean find(T value) {
        if (value == null || this.rootNode == null) return false;
        AVLNode<T> cur = this.rootNode;
        while (cur != null) {
            if (cur.data.compareTo(value) == 0) return true;
            if (value.compareTo(cur.data) < 0) cur = cur.left;
            else cur = cur.right;
        }
        return false;
    }

    /**
     * 删除元素
     *
     * @param value 待删除的元素
     * @return 删除成功--true，否则--false
     */
    public boolean remove(T value) {
        if (value == null || this.rootNode == null) return false;
        RemoveResult<T> removeResult = remove(this.rootNode, value);
        if (removeResult.success) this.rootNode = removeResult.retNode;
        return removeResult.success;
    }

    /**
     * 中序打印AVL树
     */
    public void inOrder() {
        inOrder(this.rootNode);
        System.out.println();
    }

    private void inOrder(AVLNode<T> root) {
        if (root != null) {
            inOrder(root.left);
            System.out.print(" " + root.data + " ");
            inOrder(root.right);
        }
    }

    /**
     * 删除某棵AVL树上某个结点，因为删除可能会更换根结点，因此需要返回删除以后的根结点
     *
     * @param root  树根结点
     * @param value 待删除的值
     * @return 成功返回new RemoveResult<>(true,新的树根节点); 否则 new RemoveResult<>(false,null)
     */
    private RemoveResult<T> remove(AVLNode<T> root, T value) {
        //如果根为空，则直接返回删除失败
        if (root == null) return new RemoveResult<>(false);

        //找到带删除的结点，删除逻辑和BST大致一样
        if (root.data.compareTo(value) == 0) {
            if (root.left == null || root.right == null) {
                --size;
                if (root.left == null) root = root.right;
                else root = root.left;
            } else {//当左右子树都不为空时，先从右子树找出最左的结点，作为新的根， 然后将其从右子树删除，
                AVLNode<T> leftMostOfRight = mostLeft(root.right);
                leftMostOfRight.right = remove(root.right, leftMostOfRight.data).retNode;
                leftMostOfRight.left = root.left;
                root = leftMostOfRight;
            }
            //如果当前结点不是要删除的，则根据大小关系，分别跳到左右子树 进行删除
        } else if (value.compareTo(root.data) < 0) {
            RemoveResult<T> removeLeft = remove(root.left, value);
            if (!removeLeft.success) return removeLeft;
            root.left = removeLeft.retNode;
        } else {
            RemoveResult<T> removeRight = remove(root.right, value);
            if (!removeRight.success) return removeRight;
            root.right = removeRight.retNode;
        }
        //最后需要调整高度和平衡性
        updateHeight(root);
        return new RemoveResult<>(true, adjustAVLTree(root));
    }

    /**
     * 找到AVL树某个结点上最左的结点
     *
     * @param root 需要搜索到的树根节点
     * @return root上最左的结点
     */
    private AVLNode<T> mostLeft(AVLNode<T> root) {
        if (root == null) return null;
        AVLNode<T> cur = root;
        for (; cur.left != null; cur = cur.left) ;
        return cur;
    }

    /**
     * 添加一个元素到AVL树，因为添加以后可能会改变树的根，所以返回添加后的新的根节点
     *
     * @param root  AVL树根节点
     * @param value 待添加的元素
     * @return 添加后的根结点
     */
    private AVLNode<T> put(AVLNode<T> root, T value) {
        if (root == null) {
            ++this.size;
            return new AVLNode<>(value);
        }
        // 如果找到某个元素和value相等，则不添加，返回
        if (root.data.compareTo(value) == 0) return null;
        if (value.compareTo(root.data) < 0) {//value小于根结点的值，则添加到左子树上，否则添加到右子树上
            AVLNode<T> newLeft = put(root.left, value);
            if (newLeft == null) return null;
            root.left = newLeft;
        } else {
            AVLNode<T> newRight = put(root.right, value);
            if (newRight == null) return null;
            root.right = newRight;
        }
        //更新高度
        updateHeight(root);

        //调整AVL树
        return adjustAVLTree(root);
    }

    /**
     * 获取某个结点的高度
     *
     * @param node 需要获取其高度的结点
     * @return AVL树某个结点的高度
     */
    private int height(AVLNode<T> node) {
        //如果树为空，则返回0，否则返回其height字段的值
        return node == null ? 0 : node.height;
    }

    /**
     * 更新某个AVL树结点的高度
     *
     * @param node 需要更新高度的AVL树结点
     */
    private void updateHeight(AVLNode<T> node) {
        //某个结点的高度是其左子树和右子树的高度的最大值 +1
        if (node != null) node.height = Math.max(height(node.left), height(node.right)) + 1;
    }

    /**
     * 获取AVL树某个结点的平衡因子
     * 平衡因子是左子树的高度减去右子树的高度
     *
     * @param node 需要获取其平衡因子的结点
     * @return AVL树某个结点的平衡因子
     */
    private int balanceFactor(AVLNode<T> node) {
        return node == null ? 0 : height(node.left) - height(node.right);
    }

    /**
     * 对AVL树的某个结点进行右旋操作
     * 右旋的逻辑是，node的左指针指向其左子树的右子树，其左子树的右指针指向node，返回node的左子树
     *
     * @param node 需要右旋的结点
     * @return 右旋操作以后的根节点
     */
    private AVLNode<T> rightRotate(AVLNode<T> node) {
        AVLNode<T> left = node.left;
        node.left = left.right;
        left.right = node;
        updateHeight(node);//先更新node的高度，然后才可以更新left的高度
        updateHeight(left);
        return left;
    }

    /**
     * 对AVL树的某个结点进行左旋操作
     * 左旋的逻辑是，node的右指针指向其右子树的左子树，其右子树的左指针指向node，返回node的右子树
     *
     * @param node 需要左旋的结点
     * @return 左旋操作以后的根节点
     */
    private AVLNode<T> leftRotate(AVLNode<T> node) {
        AVLNode<T> right = node.right;
        node.right = right.left;
        right.left = node;
        updateHeight(node);
        updateHeight(right);
        return right;
    }

    /**
     * 调整AVL树，主要是根据平衡因子进行旋转操作
     *
     * @param root 待调整的根节点
     * @return 调整之后的根节点
     */
    private AVLNode<T> adjustAVLTree(AVLNode<T> root) {
        if (root == null) return null;

        //判断是否平衡，如果平衡，则直接返回根节点
        int balanceFactor = balanceFactor(root);
        if (Math.abs(balanceFactor) <= 1) return root;

        //否则根据各种不平衡的情况，采取左旋和右旋进行调整
        if (balanceFactor > 1) {//当平衡因子大于1时，需要右旋解决

            // 如果根的左子树的平衡因子小于0 则说明根的左子树 右重左轻 需要先对其左旋
            if (balanceFactor(root.left) < 0) root.left = leftRotate(root.left);
            root = rightRotate(root);
        } else {//当平衡因子小于-1时，需要左旋解决

            // 如果根的左右树的平衡因子大于0 则说明根的右子树 左重右轻 需要先对其右旋
            if (balanceFactor(root.right) > 0) root.right = rightRotate(root.right);
            root = leftRotate(root);
        }
        return root;
    }

    private static class AVLNode<T extends Comparable<T>> {
        T data;
        AVLNode<T> left;
        AVLNode<T> right;
        int height;

        public AVLNode(T data) {
            this.data = data;
            this.height = 1;
        }
    }

    /**
     * 删除结果类
     *
     * @param <T>
     */
    private static class RemoveResult<T extends Comparable<T>> {
        boolean success; //当前删除是否成功
        AVLNode<T> retNode; // 删除成功后 返回的新的根结点

        public RemoveResult(boolean success, AVLNode<T> retNode) {
            this.success = success;
            this.retNode = retNode;
        }

        public RemoveResult(boolean success) {
            this(success, null);
        }
    }

    public static void main(String[] args) {
        automationTest();
    }

    /**
     * 手动测试
     */
    private static void artificialTest() {
        AVLTree<Integer> integerAVLTree = new AVLTree<>();
        Scanner sc = new Scanner(System.in);
        String command = null;
        int n;
        while (true) {
            command = sc.next();
            if ("put".equals(command)) {
                n = sc.nextInt();
                if (integerAVLTree.put(n)) System.out.println(n + " 插入成功");
                else System.out.println(n + " 插入失败");
            }
            if ("remove".equals(command)) {
                n = sc.nextInt();
                if (integerAVLTree.remove(n)) System.out.println(n + " 删除成功");
                else System.out.println(n + " 删除失败");
            }
            if ("print".equals(command)) {
                integerAVLTree.inOrder();
            }
            if ("find".equals(command)) {
                n = sc.nextInt();
                if (integerAVLTree.find(n)) System.out.println(n + " 存在当前树中");
                else System.out.println(n + " 不存在当前树中");
            }
            if ("size".equals(command)) System.out.println("当前树的结点个数是：" + integerAVLTree.size());
            if ("exit".equals(command)) break;
        }
    }

    private static volatile boolean runFlag = true;

    /**
     * 自动测试
     */
    private static void automationTest() {

        new Thread(() -> {
            //验证的逻辑是 设置一个set集合，每次生成一个随机数number，
            // 1. 测试put方法  如果set集合已经包含number的时候，说明AVLTree已经添加过这个数了，再次添加会失败，校验添加是否失败
            //                如果set集合不包含number，则认为AVLTree没有添加过这个数，测试添加是否成功

            //2. 测试remove方法 如果set集合已经包含number的时候，说明AVLTree已经添加过这个数了，测试remove是否成功
            //                  如果set集合不包含number，则认为AVLTree没有添加过这个数，测试remove是否失败

            //3. 测试find 如果set集合已经包含number的时候，说明AVLTree已经添加过这个数了，测试find是否成功
            //                   如果set集合不包含number，则认为AVLTree没有添加过这个数，测试find是否失败
            Set<Integer> integerSet = new HashSet<>();
            AVLTree<Integer> integerAVLTree = new AVLTree<>();
            int cnt = 0;
            int command, number;
            while (runFlag) {
                command = (int) (Math.random() * 4) + 1;
                number = (int) (Math.random() * Integer.MAX_VALUE) + 1;
                switch (command) {
                    case 1://put
                        if (integerAVLTree.size() < 10000) {
                            boolean put = integerAVLTree.put(number);
                            if (integerSet.contains(number)) {
                                if (put) {//如果set中已经有了，但还是添加成功了，这是不正确的
                                    System.out.println("hash表中已经包含了：" + number + " 应该添加失败，但是添加成功了");
                                    return;
                                }
                            } else {
                                if (!put) {
                                    System.out.println("hash表中没有包含：" + number + " 应该添加成功，但是添加失败了");
                                    return;
                                }
                                integerSet.add(number);
                                ++cnt;
                            }
                        }
                        break;
                    case 2://remove
                        boolean remove = integerAVLTree.remove(number);
                        if (integerSet.contains(number)) {
                            if (!remove) {
                                System.out.println("hash表中已经包含了：" + number + " 应该删除成功，但是删除失败了");
                                return;
                            }
                            --cnt;
                            integerSet.remove(number);
                        } else {
                            if (remove) {
                                System.out.println("hash表中没有包含：" + number + " 应该删除失败，但是删除成功了");
                                return;
                            }
                        }
                        break;
                    case 3://find
                        if (integerSet.contains(number)) {
                            boolean b = integerAVLTree.find(number);
                            if (!b) {
                                System.out.println("hash表中已经包含了：" + number + " 应该查找成功，但是查找失败了");
                                return;
                            }
                        }
                        break;
                    case 4://size
                        if (integerAVLTree.size() != cnt) {
                            System.out.println("size应该是:" + cnt + "，但实际上它是" + integerAVLTree.size());
                            return;
                        }
                        break;
                }
            }
        }).start();

        Scanner scanner = new Scanner(System.in);
        String next = scanner.next();
        if ("exit".equals(next)) runFlag = false;
    }
}