文章目录
线性回归
1.1 专栏介绍
??本专栏学习材料为吴恩达《机器学习》课程,希望自学吴恩达的课程后通过自己的语言对算法进行描述且加强自己对模型的理解,后续在本科课程系统学习机器学习课程后,会对自学的笔记进行修改和补充,同时希望大神们及时批评与指正。
1.2 单变量线性回归
1.2.1 模型表示
课程中吴恩达老师以房屋交易问题为例,训练集如图所示:
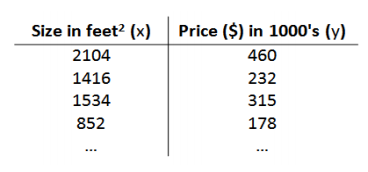
我们希望通过这些数据来预测房价,我们需要对一些符号进行定义。
| 符号 | 意义 |
|---|---|
| m m m | 训练集中实例个数 |
| x x x | 特征/输入变量 |
| y y y | 目标/输出变量 |
| ( x , y ) (x, y) (x,y) | 训练集中的实例 |
| ( x ( i ) , y ( i ) ) (x^{(i)}, y^{(i)}) (x(i),y(i)) | 第 i i i个实例 |
| h h h | 学习算法的解决方案/假设 |
因为本例中的特征只有房屋大小,价格暂时只考虑与房屋大小有关,所以称此模型为单变量线性回归,而我们对数据的处理方法大概如下所示。
数据集
学习算法
h 假设函数
输入
输出
在此例中,我们该如何选择
h
h
h呢?
因为该例只有一个特征,即房屋尺寸大小,所以我们可将假设函数设为
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta(x) = \theta_0 +\theta_1x
hθ?(x)=θ0?+θ1?x
h
h
h表示一个函数,输入的是房屋的尺寸大小,
h
h
h 根据输入的
x
x
x 值来得出
y
y
y 值,
y
y
y 值对应房屋出售价格,因此,
h
h
h 是一个从
x
x
x 到
y
y
y 的函数映射。
1.2.2 代价函数
??在设计假设函数
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta(x) = \theta_0 +\theta_1x
hθ?(x)=θ0?+θ1?x 的过程也是直线拟合散点图的过程。确定假设函数也就是我们需要选择合适的
θ
0
\theta_0
θ0? 与
θ
1
\theta_1
θ1? ,也就是图像上直线的截距与斜率。我们选择的参数决定了我们得到的直线相对于我们的训练集的准确程度,模型预测值与实际值的差距也就是建模误差。
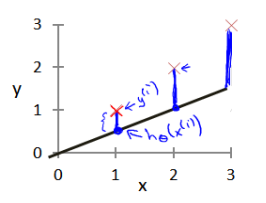
??我们的目标便是选择出可以使得建模误差的平方和能够最小的模型参数。在这里我们命名一种代价函数来表示模型误差。
m
i
n
i
m
i
z
e
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
minimize\quad J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2
minimizeJ(θ0?,θ1?)=2m1?i=1∑m?(hθ?(x(i))?y(i))2
??代价函数又叫平方误差函数,解决回归问题,平方误差函数是一种常用手段。我们可以编程将参数
θ
0
\theta_0
θ0? 、
θ
1
\theta_1
θ1?与代价函数
J
J
J的关系可视化。
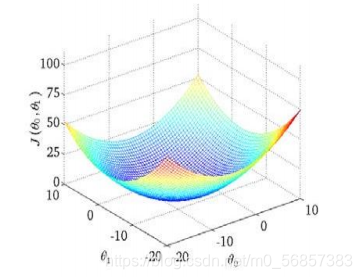
??可以看出,会有一组参数
(
θ
0
,
θ
1
)
(\theta_0, \theta_1)
(θ0?,θ1?) 使得
J
J
J 处于最低点,也就是我们希望的误差最小的参数对。幸运的是,可以通过数学证明线性回归的代价函数总为凸函数,需要用到引理:二阶可微函数为严格凸函数的充要条件为黑塞矩阵为正定矩阵,因此我们总能在线性回归的代价函数找到唯一的极小值点。接下来我们需要探索一种可以自动找到最佳参数的方法。
1.2.3 梯度下降法
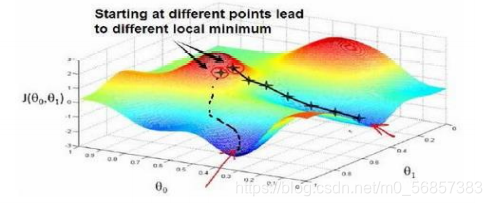
??梯度下降是一个用来求函数最小值的算法,我们会用该算法对本例假设函数进行最小化处理。该算法的思想大致为:首先随机选择一个参数组合
(
θ
0
,
θ
1
,
…
,
θ
n
)
(\theta_0, \theta_1, …, \theta_n)
(θ0?,θ1?,…,θn?),计算代价函数,接着寻找下一个能让代价函数下降最多的参数组合,直到找到局部最低点为止。而我们不能确定该局部最低点是否为全局最低点,且不同的初始参数组合可能会有不同的局部最低点。
批量梯度下降(batch gradient descent)算法的公式为:
r
e
p
e
a
t
?
u
n
t
i
l
?
c
o
n
v
e
r
g
e
n
c
e
:
θ
j
=
θ
j
?
α
?
?
?
θ
j
J
(
θ
0
,
θ
1
)
(
f
o
r
?
j
=
0
?
a
n
d
?
j
=
1
)
repeat\ until\ convergence:\\ \theta_j = \theta_j -\alpha \cdot \frac{\partial }{\partial \theta_j}J(\theta_0, \theta_1)(for\ j=0 \ and\ j=1)
repeat?until?convergence:θj?=θj??α??θj???J(θ0?,θ1?)(for?j=0?and?j=1)
??其中
α
\alpha
α 为学习率,它决定代价函数下降程度最大方向向下迈出的步子有多大。在批量梯度下降中,我们每一次迭代让所有参数减去学习率乘代价函数的导数,直至
θ
\theta
θ 收敛。
注意: 我们需要同时更新所有参数
θ
\theta
θ
t e m p 0 = θ 0 ? α ? ? ? θ 0 J ( θ 0 , θ 1 ) temp0 = \theta_0 -\alpha \cdot \frac{\partial}{\partial \theta_0}J(\theta_0,\theta_1) temp0=θ0??α??θ0???J(θ0?,θ1?)
t e m p 1 = θ 1 ? α ? ? ? θ 1 J ( θ 0 , θ 1 ) temp1 = \theta_1 -\alpha \cdot \frac{\partial}{\partial \theta_1}J(\theta_0,\theta_1) temp1=θ1??α??θ1???J(θ0?,θ1?)
θ 0 = t e m p 0 \theta_0 = temp0 θ0?=temp0
θ 1 = t e m p 1 \theta_1 = temp1 θ1?=temp1
??我们对
α
\alpha
α 有一定要求,若
α
\alpha
α 过大,可能导致其无法收敛甚至发散,若
α
\alpha
α 过小,则收敛速度会很慢。若已到达局部极值点,
?
?
θ
J
(
θ
0
,
θ
1
)
=
0
\frac{\partial}{\partial \theta}J(\theta_0,\theta_1)=0
?θ??J(θ0?,θ1?)=0,
θ
\theta
θ不再改变。
??让我们把梯度下降法利用在线性回归上,则有如下公式:
r
e
p
e
a
t
?
u
n
t
i
l
?
c
o
n
v
e
r
g
e
n
c
e
:
θ
0
=
θ
0
?
α
?
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
θ
1
=
θ
1
?
α
?
1
m
∑
i
=
1
m
[
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
?
x
(
i
)
]
u
p
d
a
t
e
?
θ
0
?
a
n
d
?
θ
1
?
s
i
m
u
l
t
a
n
e
o
u
s
l
y
repeat\ until\ convergence:\\ \theta_0 = \theta_0 -\alpha \cdot \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})\\ \theta_1 = \theta_1 -\alpha \cdot \frac{1}{m}\sum_{i=1}^m[(h_\theta(x^{(i)})-y^{(i)})\cdot x^{(i)}]\\ update\ \theta_0 \ and\ \theta_1\ simultaneously
repeat?until?convergence:θ0?=θ0??α?m1?i=1∑m?(hθ?(x(i))?y(i))θ1?=θ1??α?m1?i=1∑m?[(hθ?(x(i))?y(i))?x(i)]update?θ0??and?θ1??simultaneously
1.3 多变量线性回归
1.3.1 多维特征
??目前为止,我们探讨了单变量特征房屋大小对房价的影响,然而实际上有更多的特征会对房价造成影响,我们需要构建一个含有多个特征变量的模型,模型特征为
(
x
1
,
x
2
,
x
3
,
…
,
x
n
)
(x_1,x_2,x_3,…,x_n)
(x1?,x2?,x3?,…,xn?),我们有新的训练集如下:
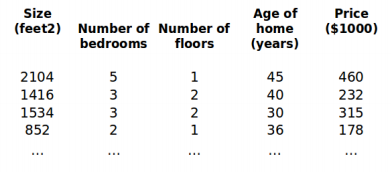
??同样地,我们需要对新的符号进行定义
| 符号 | 意义 |
|---|---|
| n n n | 特征数量 |
| x ( i ) x^{(i)} x(i) | 第 i i i个训练实例向量 |
| x j ( i ) x^{(i)}_j xj(i)? | 第 i i i个训练实例的第 j j j个特征 |
??此时支持多变量的假设函数
h
h
h为:
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
…
+
θ
n
x
n
h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n
hθ?(x)=θ0?+θ1?x1?+θ2?x2?+…+θn?xn?
??这个公式有n+1个参数和n个变量,为了使公式更加简单,我们可以引入新变量
x
0
=
1
x_0=1
x0?=1 ,则公式转化为:
h
θ
(
x
)
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
…
+
θ
n
x
n
h_\theta(x)=\theta_0x_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n
hθ?(x)=θ0?x0?+θ1?x1?+θ2?x2?+…+θn?xn?
??此时模型中的参数
θ
\theta
θ 是一个n+1维向量,而训练实例
x
x
x 也是n+1维向量,有如下表示:
θ
=
[
θ
0
θ
1
θ
2
…
θ
n
]
\theta= \begin{bmatrix} \theta_0\\ \theta_1\\ \theta_2\\ …\\ \theta_n \end{bmatrix}
θ=???????θ0?θ1?θ2?…θn?????????
X
=
[
x
0
x
1
x
2
…
x
m
]
X= \begin{bmatrix} x_0\\ x_1\\ x_2\\ …\\ x_m\\ \end{bmatrix}
X=???????x0?x1?x2?…xm?????????
??故假设函数
h
h
h 可简化为:
h
θ
(
x
)
=
θ
T
X
h_\theta(x)=\theta^TX
hθ?(x)=θTX
??其中上标T表示矩阵转置.
1.3.2 多元梯度下降
??与单变量线性回归类似,在多变量线性回归中,我们同样构建一个代价函数,则这个代价函数是所有建模误差的平方和,即:
m
i
n
i
m
i
z
e
J
(
θ
0
,
θ
1
,
…
,
θ
n
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
minimize\quad J(\theta_0,\theta_1,…,\theta_n)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2
minimizeJ(θ0?,θ1?,…,θn?)=2m1?i=1∑m?(hθ?(x(i))?y(i))2
其中
h
θ
(
x
)
=
θ
T
X
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
…
+
θ
n
x
n
h_\theta(x)=\theta^TX=\theta_0+\theta_1x_1+\theta_2x_2+…+\theta_nx_n
hθ?(x)=θTX=θ0?+θ1?x1?+θ2?x2?+…+θn?xn?.
??我们的目标与单变量线性回归时一样,找到使得代价函数最小的参数。多变量线性回归的算法为:
r
e
p
e
a
t
?
u
n
t
i
l
?
c
o
n
v
e
r
g
e
n
c
e
:
θ
j
=
θ
j
?
α
?
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
?
x
(
i
)
s
i
m
u
l
t
a
n
e
o
u
s
l
y
?
u
p
d
a
t
e
?
θ
j
?
f
o
r
?
j
=
0
,
1
,
…
,
n
repeat\ until\ convergence:\\ \theta_j=\theta_j-\alpha\cdot \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})\cdot x^{(i)}\\ simultaneously\ update\ \theta_j \ for \ j=0,1,…,n
repeat?until?convergence:θj?=θj??α?m1?i=1∑m?(hθ?(x(i))?y(i))?x(i)simultaneously?update?θj??for?j=0,1,…,n
??注意上式的
j
j
j 从0开始,因为我们引入了
x
0
=
1
x_0=1
x0?=1 ,使得算法对每一个参数
θ
\theta
θ 都成立.
1.3.3 特征缩放
??在我们面对多维特征问题的时候,我们要保证这些特征都具有相近的尺度,这将帮助梯度下降算法更快地收敛。
??以房价问题为例,假设我们使用两个特征,房屋的尺寸和房间的数量,尺寸的值为 0-2000 平方英尺,而房间数量的值则是 0-5,两个特征绝对值取值差异非常的大,以两个参数分别为横纵坐标,绘制代价函数的等高线图能,看出图像会显得很扁,梯度下降算法需要非常多次的迭代才能收敛。
??我们解决的方法为尽量使得每个特征的取值范围为-1到1之间.
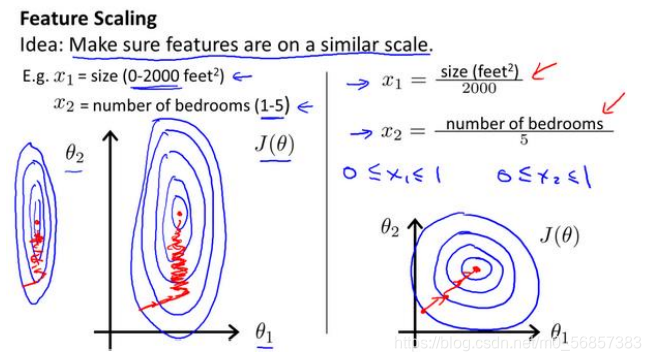
??更一般的情况,我们会利用标准差标准化公式:
x
n
=
x
n
?
μ
n
s
n
x_n=\frac{x_n-\mu_n}{s_n}
xn?=sn?xn??μn??
??其中
μ
n
\mu_n
μn? 为平均值,
s
n
s_n
sn?为标准差.
1.3.4 关于学习率
??我们不能提前预知梯度下降法的迭代次数,但可以通过可视化,找到代价函数
J
(
θ
)
J(\theta)
J(θ) 与 迭代次数的关系,帮助我们判断是否接近收敛。我们希望代价函数
J
(
θ
)
J(\theta)
J(θ) 在每一次迭代后都会下降。
??与此同时,有一种可自动判断收敛的方法,即如果代价函数
J
(
θ
)
J(\theta)
J(θ) 在一次迭代后下降少于
ε
\varepsilon
ε,则其收敛。这种方法的
ε
\varepsilon
ε 较小,比如
1
0
?
3
10^{-3}
10?3,但因
ε
\varepsilon
ε 不好取值,因此可视化判断收敛程度更佳。
??在单变量线性回归中,我们讨论过学习率对于梯度下降收敛的影响,如果
α
\alpha
α 过小,则达到收敛所需要的迭代次数会非常高;若
α
\alpha
α 过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
??通常可以尝试一些学习率:0.01,0.03,0.1,0.3,1,3……
1.3.5 特征与多项式回归
??有时候训练集给出的特征并不能很好地表现出与目标变量的影响,需要我们自己处理过后得到新的特征变量来描述关系。比如房价预测问题中,训练集给出房子的长度和宽度两个特征,不如直接用其乘积得到面积来体现与房价的关系,从而减少参数也更加直接。使得原本的假设函数
h
θ
(
x
)
=
θ
0
+
θ
1
?
w
i
d
t
h
+
θ
2
?
l
e
n
g
t
h
h_\theta(x)=\theta_0 + \theta_1\cdot width+\theta_2\cdot length
hθ?(x)=θ0?+θ1??width+θ2??length
变为
h
θ
(
x
)
=
θ
0
+
θ
1
?
a
r
e
a
h_\theta(x)=\theta_0 + \theta_1\cdot area
hθ?(x)=θ0?+θ1??area
??有时线性回归并不适用于所有数据,有时更需要曲线来进行拟合,此时可以利用多项式回归这一思想,比如用二次函数来拟合。通常我们需要先可视化观察散点图后再判断准备用什么模型去尝试,之后对该模型进行转换,可化为线性模型。
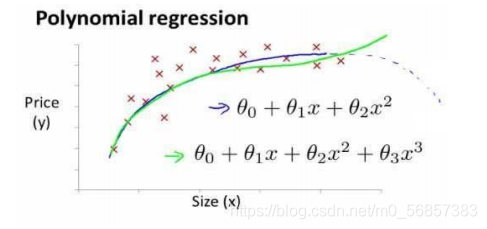
??同样地,我们仍以房屋大小为特征变量,房价为目标变量为例。当我们想用三次函数模型时,可以令
x
0
=
1
,
x
1
=
x
,
x
2
=
x
2
,
x
3
=
x
3
x_0=1,x_1=x,x_2=x^2,x_3=x^3
x0?=1,x1?=x,x2?=x2,x3?=x3,这样就又化为我们的线性回归模型。
??根据训练集所构建的散点图,我们还可以使:
h
θ
(
x
)
=
θ
0
+
θ
1
?
s
i
z
e
+
θ
2
?
s
i
z
e
h_\theta(x)= \theta_0+\theta_1\cdot size+\theta_2\cdot \sqrt{size}
hθ?(x)=θ0?+θ1??size+θ2??size?
注意:在多项式回归时,我们利用平方关系、立方关系作为新的特征变量,此时变量取值差异十分明显,应更注重特征缩放这一环节。
1.3.6 正规方程
??我们之前在寻找最合适的参数
θ
\theta
θ 时,所用的算法是梯度下降法,但在有的时候有一种叫做正规方程的方法可以不需要迭代更快地解出
θ
\theta
θ.
??正规方程法通过求解
?
?
θ
J
(
θ
)
=
0
\frac{\partial}{\partial \theta}J(\theta)=0
?θ??J(θ)=0,得到合适的
θ
\theta
θ.假设我们的训练集特征矩阵为
X
X
X (包含了
x
0
=
1
x_0=1
x0?=1),目标向量为
y
y
y,则利用正规方程解出向量
θ
=
(
X
T
X
)
?
1
X
T
y
\theta = (X^TX)^{-1}X^Ty
θ=(XTX)?1XTy
??我们对此进行以下简单推导:
由
已
知
可
得
,
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
其
中
,
h
θ
(
x
)
=
θ
T
X
=
θ
0
x
0
+
θ
1
x
1
+
…
+
θ
n
x
n
由已知可得,J(\theta)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2 \\ 其中,h_\theta(x)=\theta^TX=\theta_0x_0+\theta_1x_1+…+\theta_nx_n \\
由已知可得,J(θ)=2m1?i=1∑m?(hθ?(x(i))?y(i))2其中,hθ?(x)=θTX=θ0?x0?+θ1?x1?+…+θn?xn?
??将标量形式转化为矩阵形式,有
J
(
θ
)
=
1
2
m
(
X
θ
?
y
)
2
=
1
2
m
(
X
θ
?
y
)
T
(
X
θ
?
y
)
=
1
2
m
(
θ
T
X
T
?
y
T
)
(
X
θ
?
y
)
=
1
2
m
(
θ
T
X
T
X
θ
?
θ
T
X
T
y
?
y
T
X
θ
+
y
T
y
)
\begin{alignedat}{1} J(\theta) &=\frac{1}{2m}(X\theta - y)^2\\ &=\frac{1}{2m}(X\theta - y)^T(X\theta - y)\\ &=\frac{1}{2m}(\theta^TX^T-y^T)(X\theta - y)\\ &=\frac{1}{2m}(\theta^TX^TX\theta-\theta^TX^Ty-y^TX\theta+y^Ty) \end{alignedat}
J(θ)?=2m1?(Xθ?y)2=2m1?(Xθ?y)T(Xθ?y)=2m1?(θTXT?yT)(Xθ?y)=2m1?(θTXTXθ?θTXTy?yTXθ+yTy)?
??接下来对
J
(
θ
)
J(\theta)
J(θ) 求偏导,需要用到以下矩阵求导法则
d
A
B
d
B
=
A
T
d
B
T
A
d
B
=
A
d
X
T
A
X
d
X
=
2
A
X
\begin{alignedat}{1} \frac{dAB}{dB}&=A^T\\ \frac{dB^TA}{dB}&=A\\ \frac{dX^TAX}{dX}&=2AX \end{alignedat}
dBdAB?dBdBTA?dXdXTAX??=AT=A=2AX?
??利用以上法则,继续对
J
(
θ
)
J(\theta)
J(θ) 求偏导,且令其为0
?
J
(
θ
)
?
θ
=
1
2
m
(
2
X
T
X
θ
?
X
T
y
?
X
T
y
?
0
)
=
1
m
(
X
T
X
θ
?
X
T
y
)
=
0
\begin{alignedat}{1} \frac{\partial J(\theta)}{\partial\theta}&=\frac{1}{2m}(2X^TX\theta-X^Ty-X^Ty-0)\\ &=\frac{1}{m}(X^TX\theta-X^Ty)\\ &=0 \end{alignedat}
?θ?J(θ)??=2m1?(2XTXθ?XTy?XTy?0)=m1?(XTXθ?XTy)=0?
??解得
θ
=
(
X
T
X
)
?
1
X
T
y
\theta = (X^TX)^{-1}X^Ty
θ=(XTX)?1XTy
??关于矩阵求导公式及原理,可浏览其他博主的文章,本文便不再详述。可以看出,正规方程法对小数据集处理起来是非常快捷有效的。让我们将梯度下降与正规方程二者做个对比。
| 梯度下降法 | 正规方程法 |
|---|---|
| 需考虑特征缩放 | 不需要 |
| 需要选择学习率 α \alpha α | 不需要 |
| 需要多次迭代 | 不需要 |
| 当特征数量 n n n 较大时仍有效 | 需要计算 ( X T X ) ? 1 (X^TX)^{-1} (XTX)?1, n n n 较大时计算时间成本高,求逆时间复杂度为 O ( n 3 ) O(n^3) O(n3),一般 n < 10000 n<10000 n<10000可以接受 |
| 适用于各种模型 | 只适用于线性模型,逻辑回归等不适用 |
??除此之外,还需要注意一点:如果 X T X X^TX XTX 不可逆,这种情况一般很少发生,那么有可能是因为训练集内有相似特征变量或者训练集内特征变量过多(比如 n > m n>m n>m),对于前者我们需要保证特征变量的线性无关性,后者可以删除一些特征或者使用正则化方法来找到参数。而且在Octave中的pinv()可以求解矩阵的伪逆,一样可以求解参数 θ \theta θ.
1.4 配套作业的Python实现
1.4.1 单变量线性回归
1. 问题背景:
??假如你是一个连锁餐厅的CEO,已有不同城市的人口与利润数据集(ex1data1.txt),第一列为人口,第二列为利润,请你使用一个变量实施线性回归来预测连锁餐厅利润。
2. 代码实现:
??导入所需要的包
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
??导入数据集,一定要把数据文件ex1data1.txt放在和程序同一个文件夹里,否则需要使用绝对路径访问文件
path = 'ex1data1.txt'
data = pd.read_csv(path, header=None, names=['Population', 'Profit'])
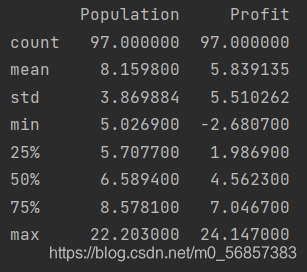
print(data.head()) # 预览数据
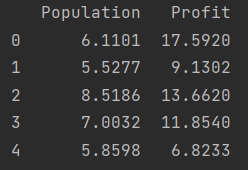
print(data.describe())
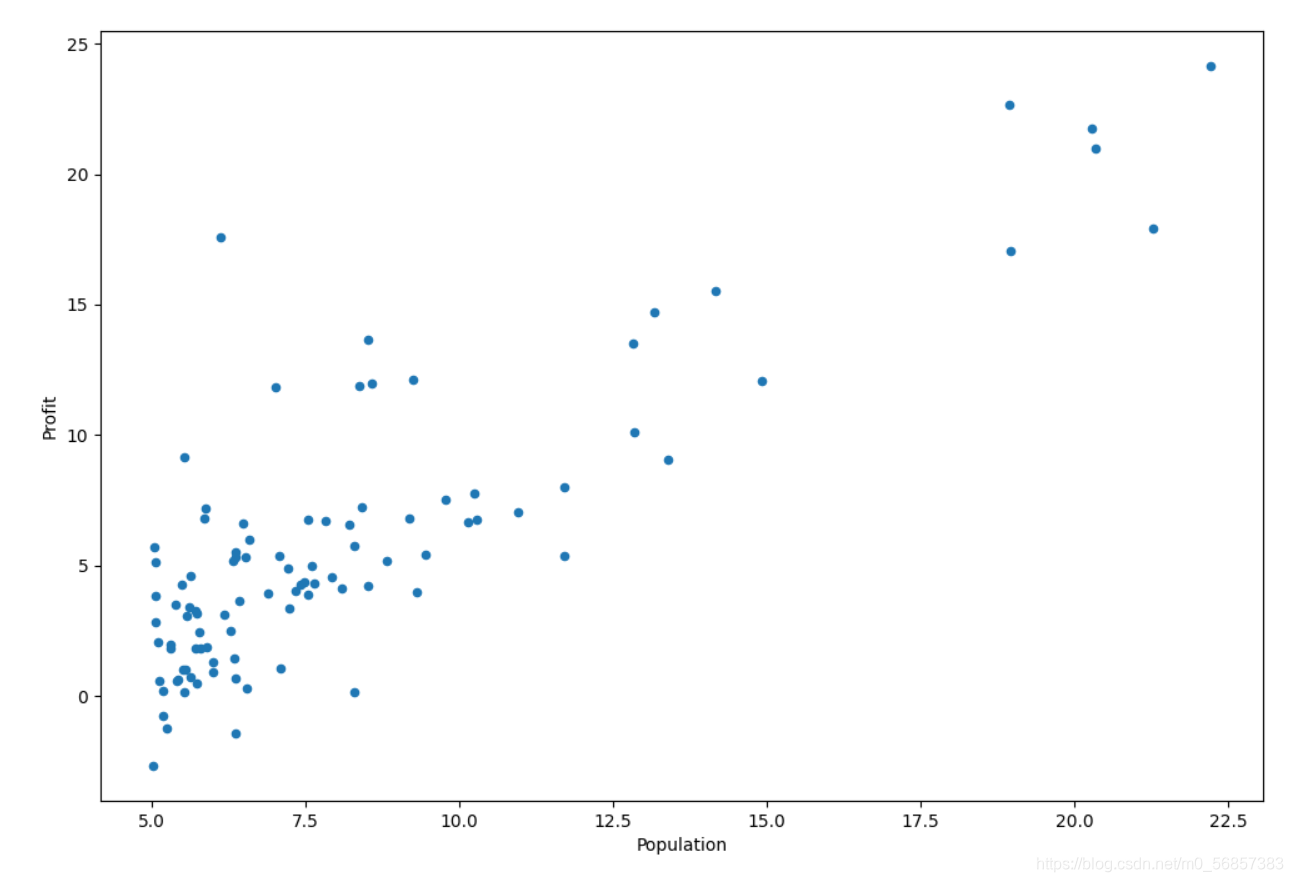
??数据可视化,绘制散点图
??可利用matplotlib库将Dataframe转为数组后plt.scatter
data_x = data["Population"].values
data_y = data["Profit"].values
plt.figure(figsize=(12,8))
plt.scatter(data_x, data_y)
plt.xlabel("Population")
plt.ylabel("Profit")
plt.show()
??也可以直接用Pandas直接作图
data.plot(kind="scatter", x="Population", y="Profit", figsize=(12, 8))
plt.show()
??梯度下降法,以实现最小化代价函数。首先需要创建代价函数
J
(
θ
0
,
θ
1
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
2
J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2
J(θ0?,θ1?)=2m1?i=1∑m?(hθ?(x(i))?y(i))2
def compute_cost(X, y, theta):
inner = np.power((X * theta.T)-y, 2)
cost = np.sum(inner)/(2*len(X))
return cost
??函数设计思路:因为
h
θ
(
x
)
=
θ
0
+
θ
1
x
h_\theta(x) = \theta_0 +\theta_1x
hθ?(x)=θ0?+θ1?x,可利用矩阵形式批量计算误差后平方累和最后除以2倍样本数。这里的矩阵形式是因为theta的维度是一个(1,2)的行向量,而y是(97,1)的列向量,因此需要把theta取转置。
??由前文可知,引入
x
0
=
1
x_0=1
x0?=1后将更方便利用矩阵处理代价函数与梯度,因此我们需要在DataFrame中引入该列。
data.insert(0, 'Ones', 1)
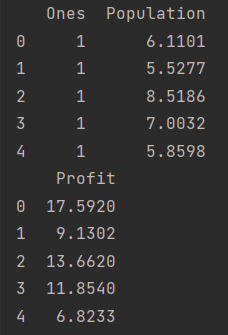
??创建好代价函数之后,我们需要处理DataFrame中的数据,使其可以直接传入compute_cost中,也就是得到所需的X,y,theta。
cols = data.shape[1]
X = data.iloc[:, 0:cols-1] # X是所有行,去掉最后一列
y = data.iloc[:, cols-1:cols] # y是所有行,最后一列
print(X.head())
print(y.head())
??我们利用切片处理数据时记得检查是否该数据是我们所需要的。
??检查完毕后,将这些Pandas数据类型转化为可传入函数的矩阵类型。
X = np.matrix(X.values)
y = np.matrix(y.values)
theta = np.matrix(np.array([0, 0]))
??转化完毕后可查看各矩阵的维度是否满足传入函数的条件。
print(X.shape, y.shape, theta.shape)
(97, 2) (97, 1) (1, 2)
??可以看出,果然与前文描述的一样,y为列向量,theta为行向量需要在函数内转置才可运算。接下来便可执行compute_cost函数,观察在
θ
0
=
0
,
?
θ
1
=
0
\theta_0=0,\ \theta_1=0
θ0?=0,?θ1?=0 的条件下的代价函数值。
print(compute_cost(X, y, theta))
32.072733877455676
??接下来是批量梯度下降的代码实现,是本节最重要的知识之一。
r
e
p
e
a
t
?
u
n
t
i
l
?
c
o
n
v
e
r
g
e
n
c
e
:
θ
j
=
θ
j
?
α
?
1
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
?
y
(
i
)
)
?
x
(
i
)
s
i
m
u
l
t
a
n
e
o
u
s
l
y
?
u
p
d
a
t
e
?
θ
j
?
f
o
r
?
j
=
0
,
1
,
…
,
n
repeat\ until\ convergence:\\ \theta_j=\theta_j-\alpha\cdot \frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})\cdot x^{(i)}\\ simultaneously\ update\ \theta_j \ for \ j=0,1,…,n
repeat?until?convergence:θj?=θj??α?m1?i=1∑m?(hθ?(x(i))?y(i))?x(i)simultaneously?update?θj??for?j=0,1,…,n
def gradientDescent(X, y, theta, alpha, iters):
temp = np.matrix(np.zeros(theta.shape))
parameters = int(theta.ravel().shape[1])
cost = np.zeros(iters)
for i in range(iters):
error = (X * theta.T) - y
for j in range(parameters):
term = np.multiply(error, X[:, j])
temp[0, j] = theta[0, j] - alpha / len(X) * np.sum(term)
theta = temp
cost[i] = compute_cost(X, y, theta)
return theta, cost
??这里运用到的temp变量是为了保证每个 θ \theta θ 同时更新,先把算出来的 θ j \theta_j θj?存起来,再把它们一起赋值给theta向量。细心的读者可以发现,这个批量梯度下降算法实际上可以直接处理多变量线性回归问题。接着,我们需要初始化学习率与迭代次数。
alpha = 0.01
iters = 1000
??最后让我们用梯度下降算法得到最新的参数 θ \theta θ.
new_theta, cost = gradientDescent(X, y, theta, alpha, iters)
print(new_theta)
[[-3.24140214 1.1272942 ]]
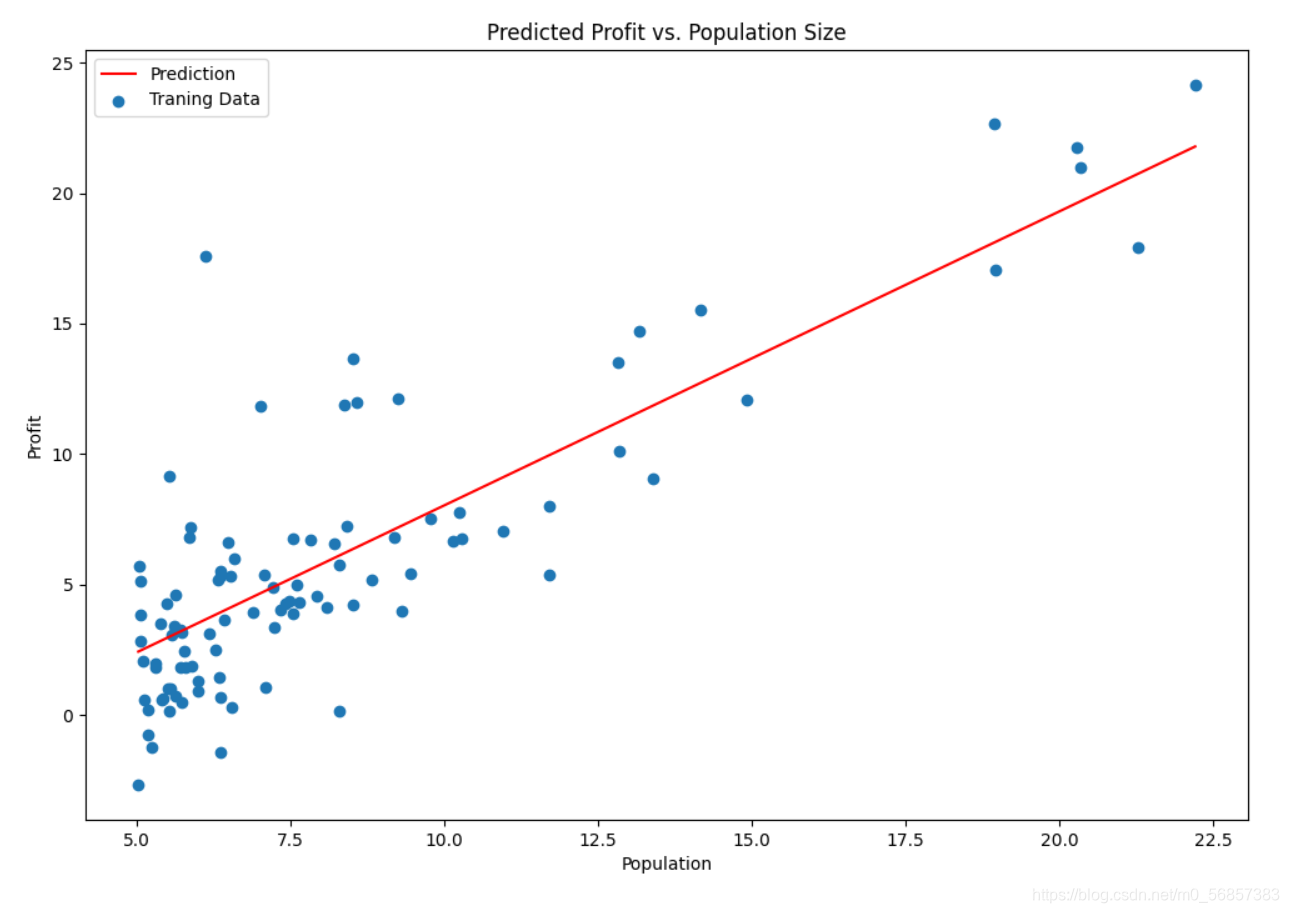
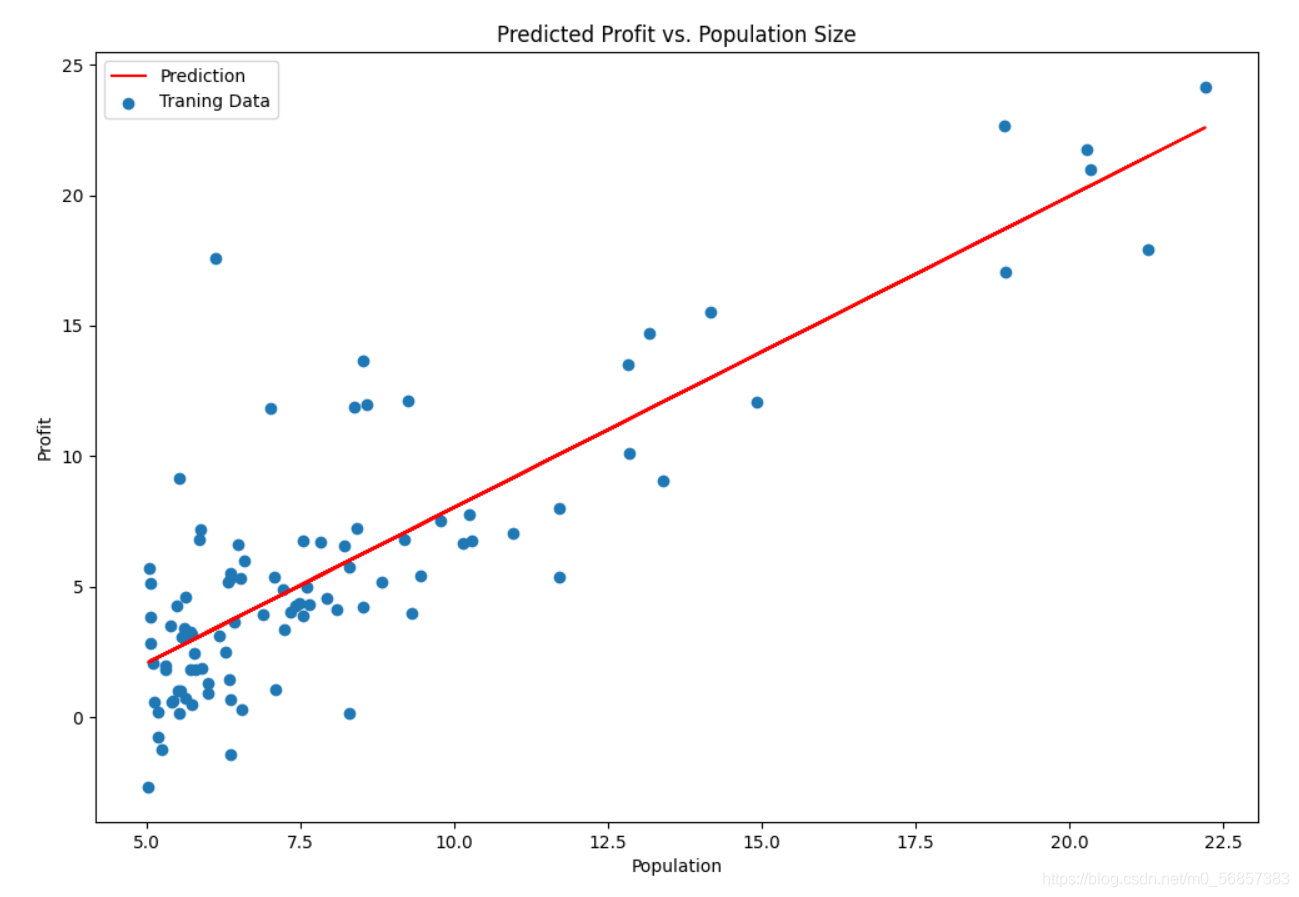
3. 可视化
??得到迭代出的参数
θ
\theta
θ 后,便可以将线性模型可视化在散点图中观察拟合效果。
x = np.linspace(data.Population.min(), data.Population.max(), 100)
f = new_theta[0, 0] + (new_theta[0, 1] * x)
fig, ax = plt.subplots(figsize=(12, 8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
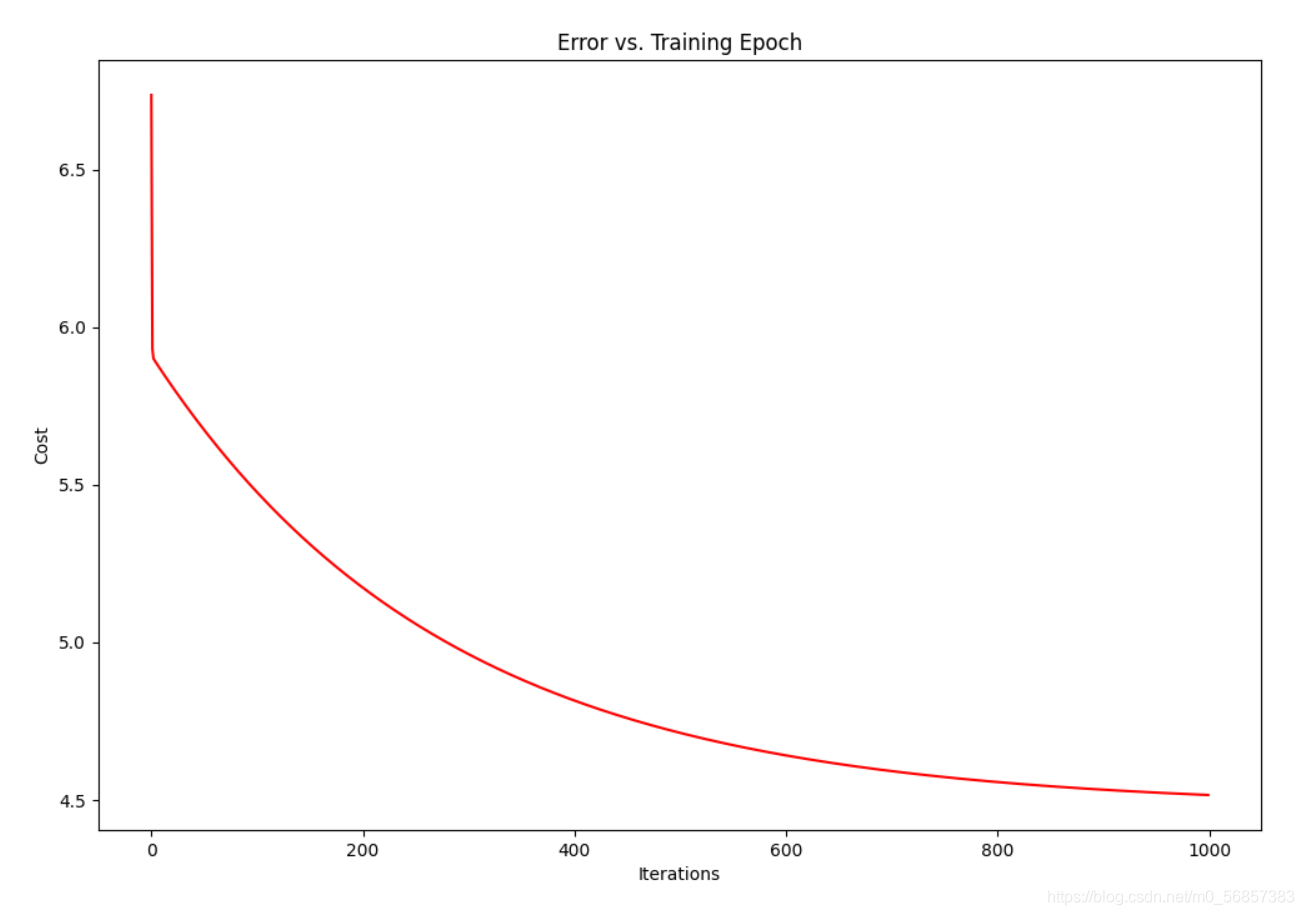
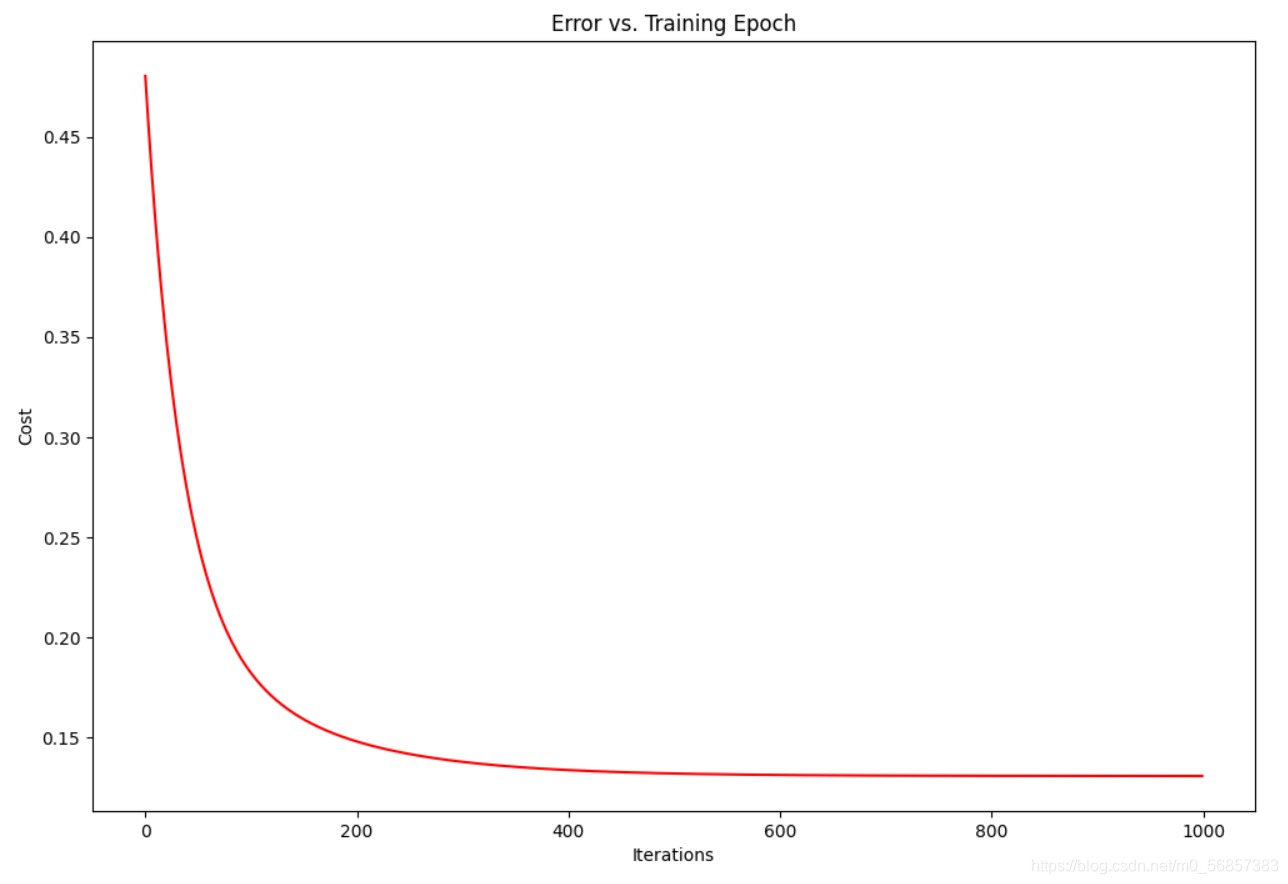
??有了结果之后,自然还可以做很多有意思的检验,做很多有趣的可视化,比如代价函数值随迭代次数的变化,观察学习率
α
\alpha
α 是否设置合理,是否每一次迭代后都有所下降以及其收敛程度。
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
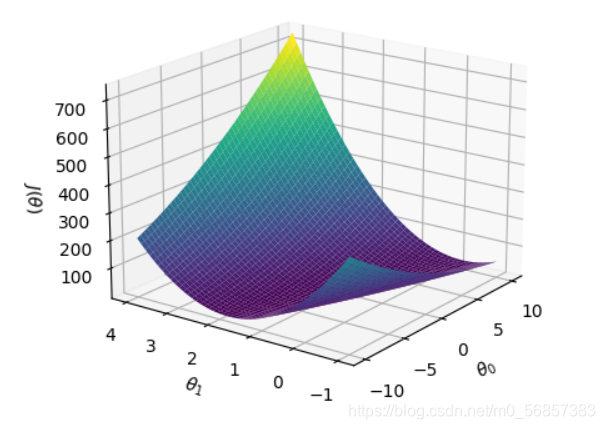
??还可以作出不同参数
θ
\theta
θ 对代价函数的影响的三维图与等高线图。
theta_0 = np.linspace(-10, 10, 50)
theta_1 = np.linspace(-1, 4, 50)
Theta_0, Theta_1 = np.meshgrid(theta_0, theta_1)
Cost = np.zeros((50, 50))
for i in range(len(theta_0)):
for j in range(len(theta_1)):
Theta = np.matrix([theta_0[i], theta_1[j]])
Cost[j][i] = compute_cost(X, y, Theta)
ax = plt.axes(projection='3d')
ax.plot_surface(Theta_0, Theta_1, Cost, cmap="viridis")
ax.set_xlabel("$\\theta_0$")
ax.set_ylabel("$\\theta_1$")
ax.set_zlabel("$J(\\theta)$")
plt.show()
theta_0 = np.linspace(-10, 10, 100)
theta_1 = np.linspace(-1, 4, 100)
[Theta_0, Theta_1] = np.meshgrid(theta_0, theta_1)
print(Theta_1)
Cost = np.zeros((100, 100))
for i in range(len(theta_0)):
for j in range(len(theta_1)):
Theta = np.matrix([theta_0[i], theta_1[j]])
Cost[j, i] = compute_cost(X, y, Theta)
plt.contour(Theta_0, Theta_1, Cost, np.linspace(5, 20, 5))
plt.xlabel("$\\theta_0$")
plt.ylabel("$\\theta_1$")
plt.scatter(new_theta[0, 0], new_theta[0, 1], marker="x")
plt.show()

1.4.2 多变量线性回归
1. 问题背景
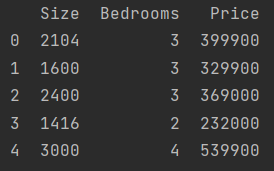
??你想要卖你的房子,你想知道什么是好的市场价格。我们收集了最近售出房屋的信息,实现一个多变量线性回归的模型。数据集为ex1data2.txt,里面包含了俄勒冈州波特兰市的房价信息,其中第一列为房子的大小(以平方英尺为单位),第二列为卧室数,第三列为房价。
2. 代码实现
??此问与第一问不同的是,该数据集的特征有两个,为多变量线性回归问题。我们依然选择使用批量梯度下降算法来解决该问题。首先仍是导入数据集ex1data2.txt.
path = 'ex1data2.txt'
data2 = pd.read_csv(path, header=None, names=['Size', 'Bedrooms', 'Price'])
print(data2.head())
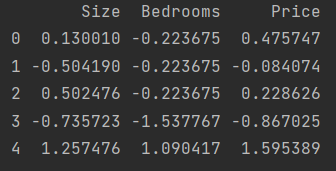
??观察该数据集,我们很容易发现上文提到的特征缩放问题,卧室数与房价的范围差距太大了,因此我们需要对该数据集进行数据预处理——特征归一化。
data2 = (data2 - data2.mean()) / data2.std()
print(data2.head())
??现在我们重复第一问单变量线性回归的步骤,对数据进行预处理。
data2.insert(0, 'Ones', 1)
cols = data2.shape[1]
X2 = data2.iloc[:, 0:cols-1]
y2 = data2.iloc[:, cols-1:cols]
X2 = np.matrix(X2.values)
y2 = np.matrix(y2.values)
theta2 = np.matrix(np.array([0, 0, 0]))
??同样地应用批量梯度下降算法,得到合适的 θ \theta θ 与 J ( θ ) m i n J(\theta)_{min} J(θ)min?.
alpha = 0.01
iters = 1000
new_theta2, cost2 = gradientDescent(X2, y2, theta2, alpha, iters)
print(compute_cost(X2, y2, new_theta2))
print(new_theta2)
0.1307033696077189
[[-1.10910099e-16 8.78503652e-01 -4.69166570e-02]]
3. 可视化
??同样地,我们也可以将训练进程可视化。
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(np.arange(iters), cost2, 'r')
ax.set_xlabel('Iterations')
ax.set_ylabel('Cost')
ax.set_title('Error vs. Training Epoch')
plt.show()
1.4.3 正规方程
??对此问题我们依然使用第二问数据集ex1data2.txt.正规方程为
θ
=
(
X
T
X
)
?
1
X
T
y
\theta = (X^TX)^{-1}X^Ty
θ=(XTX)?1XTy
def normalEqn(X, y):
theta = np.linalg.inv(X.T@X)@X.T@y
return theta
final_theta = normalEqn(X2, y2)
print(final_theta.T)
[[-1.10910099e-16 8.78503652e-01 -4.69166570e-02]] # 梯度下降
[[-1.11022302e-16 8.84765988e-01 -5.31788197e-02]] # 正规方程
??可以发现,梯度下降的结果与正规方程有一定差距,原因可能是迭代次数不够等等。
1.4.4 线性回归的scikit-learn实现
??我们利用第一问的数据集ex1data1.txt,使用scikit-learn库实现。
from sklearn import linear_model
model = linear_model.LinearRegression()
model.fit(X, y)
x = np.array(X[:, 1].A1)
f = model.predict(X).flatten()
fig, ax = plt.subplots(figsize=(12,8))
ax.plot(x, f, 'r', label='Prediction')
ax.scatter(data.Population, data.Profit, label='Traning Data')
ax.legend(loc=2)
ax.set_xlabel('Population')
ax.set_ylabel('Profit')
ax.set_title('Predicted Profit vs. Population Size')
plt.show()
??以上,便是DS的machine learning学习笔记的第一节:线性回归的全部内容,由于是自学吴恩达课程,会有不严谨甚至错误的地方,欢迎大家指出。在本科系统学习《机器学习》课程后会对该节进行修改更新。下一节内容为逻辑回归。