[数据结构与算法]剑指offer-21~30（基础必会！）

21. 调整数组顺序使奇数位于偶数前面

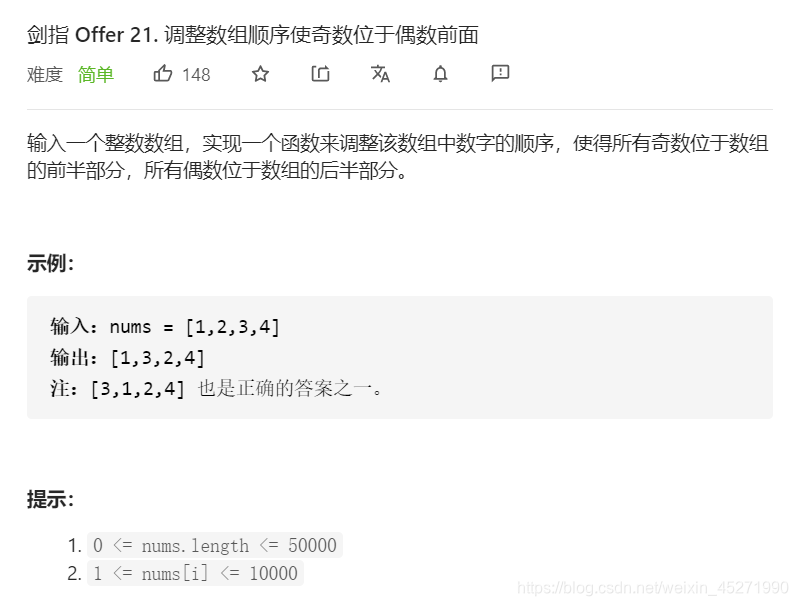
思路使用双指针法
思路一：首尾双指针

注意判断数组的引用指向，老是忘，该打！

class Solution {
    public int[] exchange(int[] arr) {
        if(arr == null || arr.length == 0) return arr;
        int left = 0;
        int right = arr.length-1;
        int key = arr[left];
        while(left < right){
            while(left < right && arr[right] %2 == 0){
                right--;
            }
            arr[left] = arr[right];
            while(left < right && arr[left] %2 != 0){
                left++;
            }
            arr[right] = arr[left];
        }
        arr[left] = key;
        return arr;
    }
}

思路二：快慢双指针

slow 的左边都是奇数，slow指向的位置应该是第一个遇到的偶数，同时fast 遇到奇数的之后和slow 指向的 值交换，
这样可以保证fast走完一遍以后 所有的奇数都在slow的左侧了>

class Solution {
    public int[] exchange(int[] nums) {
        if(nums == null || nums.length == 0) return nums;
        int slow = 0;
        int fast = 0;
        while(slow < nums.length && fast < nums.length){
            while(slow < nums.length  && nums[slow] %2 != 0){
                slow++;
                fast++;
            } //这里找到了第一个偶数
            while(fast < nums.length && nums[fast] % 2== 0){
                fast++;
            }//这里找到了一个奇数
            //执行交换的逻辑
            if(slow < nums.length && fast < nums.length){
                int temp = nums[slow];
                nums[slow] = nums[fast];
                nums[fast] = temp;
            }
        }
        return nums;
    }
}

这两种写法其实和快排的逻辑是一样的

22. 链表中倒数第K个结点

注意这里需要对k进行数据的判断，所以需要先求出链表的长度（但是这个题看题意就不用了，不会越界的）
下面给出特判k 和不特判k的快慢指针的写法

快指针先走k-1 步，之后和慢指针一起一步步的走，直到快指针走到了链表的尾部，返回慢指针所在的位置，就是此时的倒数第k个结点。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        ListNode cur = head;
        //让fast 先走key-1步
        ListNode fast = head;
        while(k - 1 > 0){
            fast = fast.next;
            k--;
        }
        while(fast.next != null){
            cur = cur.next;
            fast = fast.next;
        }

        return cur;
    }
}

求出链表的长度 对k进行取模，然后特殊设置，如果恰好是第一个倒数第length 个，注意就好啦

class Solution {
    public ListNode getKthFromEnd(ListNode head, int k) {
        ListNode cur = head;
        int length = 0;
        if(head == null) return null;
        while(cur != null){
            cur = cur.next;
            length++;
        }
        int key = k%length;
        if(key == 0) key = length; //如果恰好是第一个倒数第length 个 取模是0 特殊赋值即可
        //让fast 先走key-1步
        ListNode fast = head;
        while(key - 1 > 0){
            fast = fast.next;
            key--;
        }
        cur = head;
        while(fast.next != null){
            cur = cur.next;
            fast = fast.next;
        }

        return cur;

    }
}

24.反转链表

没有23题，不是我没写，是真的leetcode 没有？

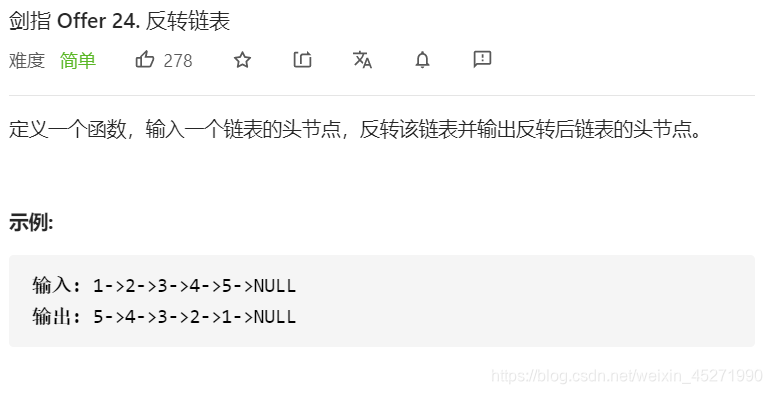
没啥题解，自己画图，定义prev cur curNext 就可以了。

class Solution {
    public ListNode reverseList(ListNode head) {
        ListNode prev = new ListNode(-1);
        prev.next = head;
        ListNode cur = head;
        if(head == null || head.next == null) return head;
        ListNode curNext = null;
        while(cur != null){
            curNext = cur.next;
            cur.next = prev;
            prev = cur;
            cur = curNext;
        }
        head.next = null;
        return prev;
    }
}

25.合并两个排序链表

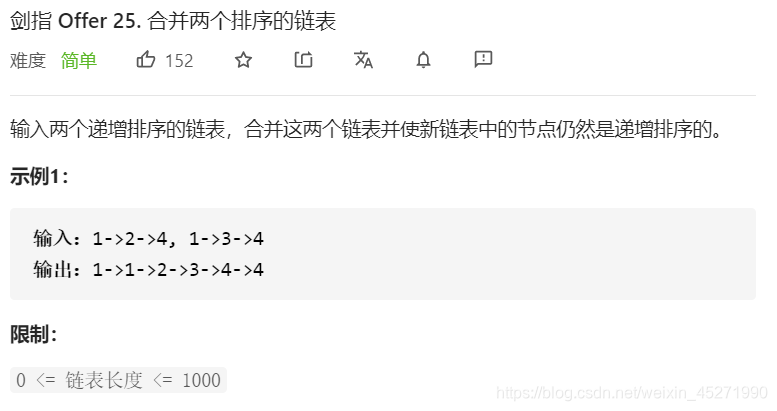
这个也没啥需要注意的，看看就好啦！
倒是有一个它的衍生题目 合并k个排序链表，值得一做！

class Solution {
    public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
        ListNode fakeHead = new ListNode(-1);
        ListNode prev = fakeHead;
        ListNode cur1 = l1;
        ListNode cur2 = l2;

        while(cur1 != null && cur2 != null){
            if(cur1.val <= cur2.val){
                prev.next =cur1;
                prev = prev.next;
                cur1 =cur1.next;
            }else{
                prev.next = cur2;
                prev = prev.next;
                cur2 = cur2.next;
            }
        }
        while(cur1 != null){
            prev.next =cur1;
            prev = prev.next;
            cur1 =cur1.next;
        }
        while(cur2 != null){
            prev.next = cur2;
            prev = prev.next;
            cur2 = cur2.next;
        }
        return fakeHead.next;
    }
}

26.树的子结构(※※)

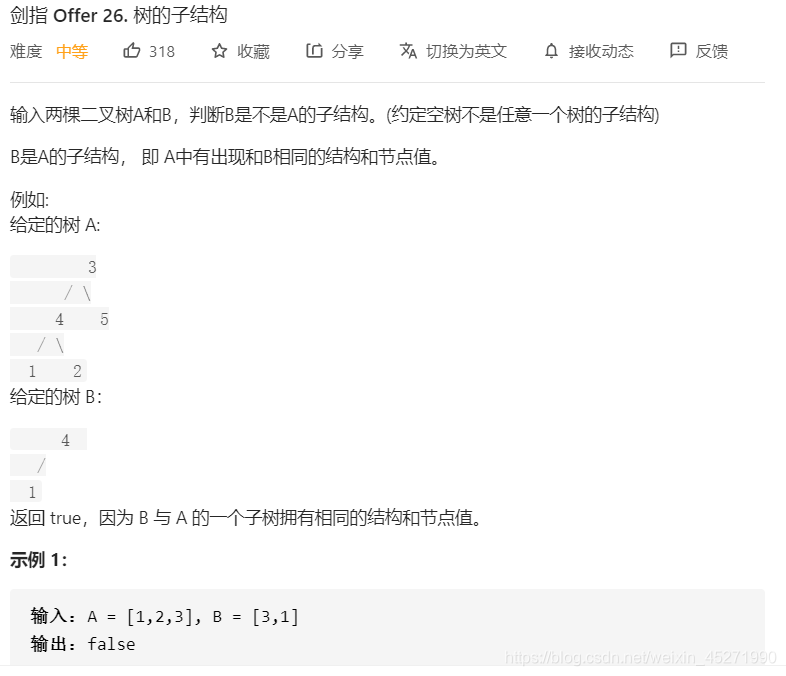
我的错误理解是找到第一个相等的值，然后去看A的左子树和B的左子树 以及A的右子树和B的右子树是否相等，但是是有问题的!

我的错误思路：
首先对树进行先序遍历，在A中找到和B的根节点相同的结点，之后在这个结点判断这个这个结点的左子树和B的左子树是不是子树关系，并且判断这个结点的右子树和B的右子树是不是子树的关系。即使找到了了相同的根节点有可能出现上面的情况，还是要去在当前的结点的左子树和右子树进行遍历。
于是写了下面这样的一段代码出来，错的，但是值得反思。

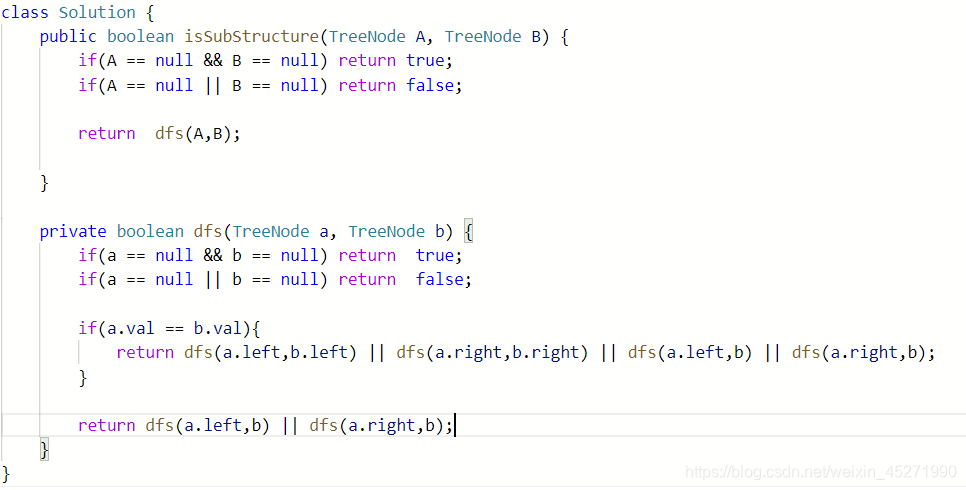
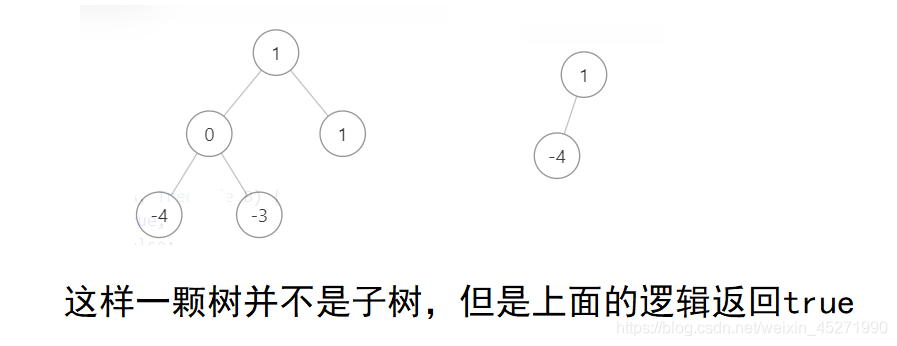
好像树的递归写多了，自己都不知道在干啥，有的题糊里糊涂就写对了，有的也不知掉为啥错了

判断B是不是树A的子结构两步逻辑

• 遍历树A的每一个结点
• 判断A 中以当前遍历到的为根节点的子树 是否包含树 B

class Solution {
    public boolean isSubStructure(TreeNode A, TreeNode B) {
        if(A== null && B == null) return true; //两个树都是空树
        if(A == null || B == null ) return false; //空树不是任意一个树的子结构

        //先判断当前的根节点的树和B是不是子树关系

        if(recur(A,B)){
            return true; //如果当前的就是那么但会true 如果不是 那么继续去左右结点找子树的关系
        }else {
            return isSubStructure(A.left,B) || isSubStructure(A.right,B);
        }
    }

    //recur 重现的意思 再发生
    private boolean recur(TreeNode a, TreeNode b) {
        //两个树同时走到了末尾 b== null && a == null || b树走到了末尾 b==null
        //传进来的时候 可以确保b不是空树 所有b为null 一定是因为递归的关系走完了 所以可以返回null
        if(b == null ) return true;

        //表明没有树了 那么自然也就不可能是子树的关系 返回fasle
        if(a == null) return false;

        if(a.val == b.val){
            return recur(a.left,b.left) && recur(a.right,b.right);
        }else {
            //如果当前的根结点的值都不相等，那么直接返回false
            return false;
        }
    }

}

27.二叉树的镜像 (※※)

思路一：递归
其实这个题目的本意是想原地改变这个树的结构，然后变成镜像的方式呈现。

根据二叉树镜像的定义，考虑递归遍历（dfs）二叉树，交换每个节点的左 / 右子节点，即可生成二叉树的镜像。
注意事先要保当前结点的一边，不然递归之后指向都变化了

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;

        //保存一下root 的left
        TreeNode left = root.left;
        root.left = mirrorTree(root.right);
        root.right = mirrorTree(left);
        return root;
    }
}

下面这个是我自己重现new 了一个树，锻炼一下思维

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;
        return dfs(root);
    }

    public TreeNode dfs(TreeNode a){
        //如果是最后一个结点了那么返回即可
        if(a == null) return null;
        if(a.left == null && a.right == null) return new TreeNode(a.val);

        //new 出当前遍历的结点
        TreeNode node = new TreeNode(a.val);
        //当前的子树关系进行建立
        node.left = dfs(a.right);
        node.right = dfs(a.left);
        return node;
    }
}

思路二：使用栈

其实还是使用的交换左右子树的思想，只不过是利用栈来解决处理结点的顺序问题

class Solution {
    public TreeNode mirrorTree(TreeNode root) {
        if(root == null) return null;
        Deque<TreeNode> stack = new LinkedList<>();
        stack.add(root);
        while(stack.size() != 0){
            TreeNode node = stack.pop();
            if(node.left != null) stack.add(node.left);
            if(node.right != null) stack.add(node.right);
            TreeNode temp = node.left;
            node.left = node.right;
            node.right = temp; 
        }
        return root;
    }
}

28.对称的二叉树

对于树中 任意两个对称节点 L和 R ，一定有：
L.val = R.val ：即此两对称节点值相等。
L.left.val = R.right.val ：即 L 的 左子节点 和 R 的 右子节点 对称；
L.right.val = R.left.val：即 LL的 右子节点 和 R 的 左子节点 对称。

递归判断即可

class Solution {
    public boolean isSymmetric(TreeNode root) {
        if(root == null) return true;
        return dfs(root.left,root.right);
    }
    //判断这棵树是不是镜像的
    public boolean dfs(TreeNode a,TreeNode b){
        if(a == null && b == null) return true;
        if(a == null || b == null) return false;

        if(a.val != b.val){
            return false;
        }else{
            return dfs(a.left,b.right) && dfs(a.right,b.left);
        }
    }
}

29.顺时打印矩阵

实在是不知道，为什么一个简单的题，还做了这么久？怀疑自己的能力了…
空值处理： 当 matrix 为空时，直接返回空列表 [] 即可。

思路一： 分别定两个坐标

一个是左上角 一个是右下角，每次打完一圈之后，改变两个定点！ 通过更新 x y 从左上角开始在来一圈

class Solution {
    public int[] spiralOrder(int[][] matrix) {
        if(matrix == null || matrix.length == 0|| matrix[0].length == 0) return new int[0];
        int level = matrix.length;
        int column = matrix[0].length;
        int length = level * column;
        int []res = new int[length];

        int leftX = 0;
        int leftY = 0;
        int rightX = matrix.length-1;
        int rightY = matrix[0].length-1;
        int x = 0;
        int y = 0;
        int i = 0;

        while(length > 0){
            if (x == leftX ){
                res[i++] = matrix[x][y];
                length--;
                y++;
                if(y > rightY) {x++;y--;}
            }
            else if (y == rightY) {
                res[i++] = matrix[x][y];
                x++;
                length--;
                if(x > rightX) {x--;y--;}
            }
            else if (x == rightX){
                res[i++] = matrix[x][y];
                y--;
                length--;
                if(y < leftY){ x--;y++;}
            }
            else if(y == leftY) {
                res[i++] = matrix[x][y];
                length--;
                x--;
                //每调整完一轮之后 定向的指针都要变化
                if(x == leftX ) {
                    leftX++;leftY++;
                    rightX--;rightY--;
                    x = leftX;
                    y = leftY;
                }
            }

        }
        return res;
    }
}

思路二：定 top bottom left right

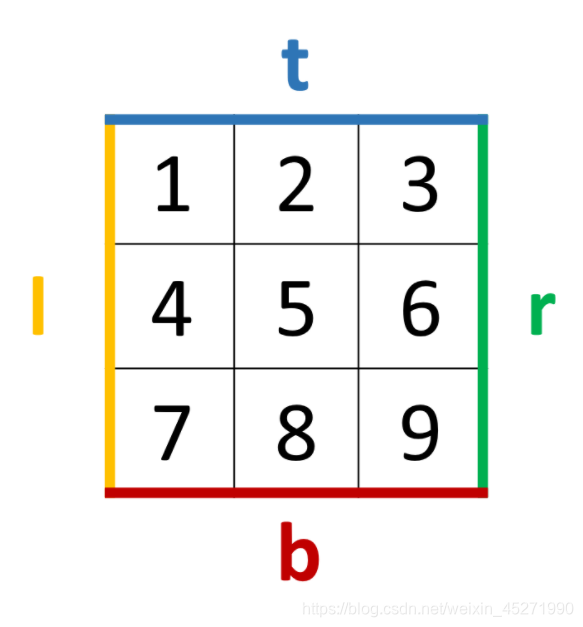
class Solution {
    public int[] spiralOrder(int[][] matrix) {
        if(matrix.length == 0) return new int[0];
        int l = 0, r = matrix[0].length - 1, t = 0, b = matrix.length - 1, x = 0;
        int[] res = new int[(r + 1) * (b + 1)];
        while(true) {
            for(int i = l; i <= r; i++) res[x++] = matrix[t][i]; // left to right.
            if(++t > b) break;
            for(int i = t; i <= b; i++) res[x++] = matrix[i][r]; // top to bottom.
            if(l > --r) break;
            for(int i = r; i >= l; i--) res[x++] = matrix[b][i]; // right to left.
            if(t > --b) break;
            for(int i = b; i >= t; i--) res[x++] = matrix[i][l]; // bottom to top.
            if(++l > r) break;
        }
        return res;
    }
}

30.包含min函数的栈

思路一：双栈解法
空间复杂度 o(n)
一个栈正常的进出 一个栈保存当前栈中的最小数据

class MinStack {
 /** initialize your data structure here. */
    Deque<Integer> stack = null;
    Deque<Integer> stackMin = null;
    public MinStack() {
        stack = new LinkedList<>();
        stackMin = new LinkedList<>();
    }
    
    public void push(int x) {
        stack.push(x);
        if(stackMin.size() == 0 || x < stackMin.peek()){
            stackMin.push(x);
        }else{
            stackMin.push(stackMin.peek());
        }
    }
    
    public void pop() {
       stack.pop();
       stackMin.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int min() {
        return stackMin.peek();
    }
}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.min();
 */

思路二：残差法。
这里就不写了，简单说一下思路。
栈里面存放的元素永远是遍历到的元素 x 和 min 的差值！

如果我们用一个最小值来记录当前栈的min，那么当min这个元素出栈的时候，需要将最小值回退的上一个版本，这个时候，如何做呢，那就是记录一个上一个和当前的差值。

class MinStack {
    /**
     * 残差法
     */
    Deque<Long> stack;
    long min;
    /** initialize your data structure here. */
    public MinStack() {
        stack = new LinkedList<>();
    }
    public void push(long x) {
        if(stack.isEmpty()){
            min = x;
            stack.push(0l);
        }else{
            stack.push(x - min);
            // 小于min则更新
            min = x < min? x: min;
        }
    }
    public void pop() {
        //看是否需要更新min
        if(stack.peek() < 0){
            //说明需要更新一下最小值
            min = min - stack.pop();
        }else {
            stack.pop();
        }
    }
    public long top() {
        //如果当前的栈顶小于0 那么top 就是min
        if(stack.peek() < 0) {
            return  min;
        }else {
            return  stack.peek() + min;
        }
    }
    public long min() {
        return min;
    }

}

/**
 * Your MinStack object will be instantiated and called as such:
 * MinStack obj = new MinStack();
 * obj.push(x);
 * obj.pop();
 * int param_3 = obj.top();
 * int param_4 = obj.min();
 */