图结构概念
图是区别于线性结构(只有一个前驱和一个后驱)和树结构(一个父节点和多个子节点)的数据结构,它是一种多对多的关系。图(Graph)是有顶点的有穷非空集合和顶点之间边的集合组成,通常表示为: G ( V , E ) G(V, E) G(V,E),其中 G G G表示图, V V V表示顶点的集合, E E E表示边的集合。
线性表中,数据元素被称为元素;树结构中,数据元素被称为节点;图结构中,数据元素被称为顶点。在线性表和树中允许为空,有空表和空树的概念,图结构中不允许为空,只有有一个顶点。在线性表中相邻元素之间具有线性关系,树中相邻层的节点具有层次关系。图中的两个顶点允许没有边的关系(即图可以允许只有顶点,边的集合可以为空)。
边可以有方向和无方向,被称为有向边或无向边。即:若顶点 v i v_i vi?到顶点 v j v_j vj?之间的边无方向称边为无向边记为 e i j = ( v i , v j ) e_{ij}=(v_i,v_j) eij?=(vi?,vj?)。若顶点 v i v_i vi?到顶点 v j v_j vj?之间的边有方向称边为有向边记为 e i j = < v i , v j > e_{ij}=<v_i,v_j> eij?=<vi?,vj?>。如下图所示左为无向图,右为有向图:
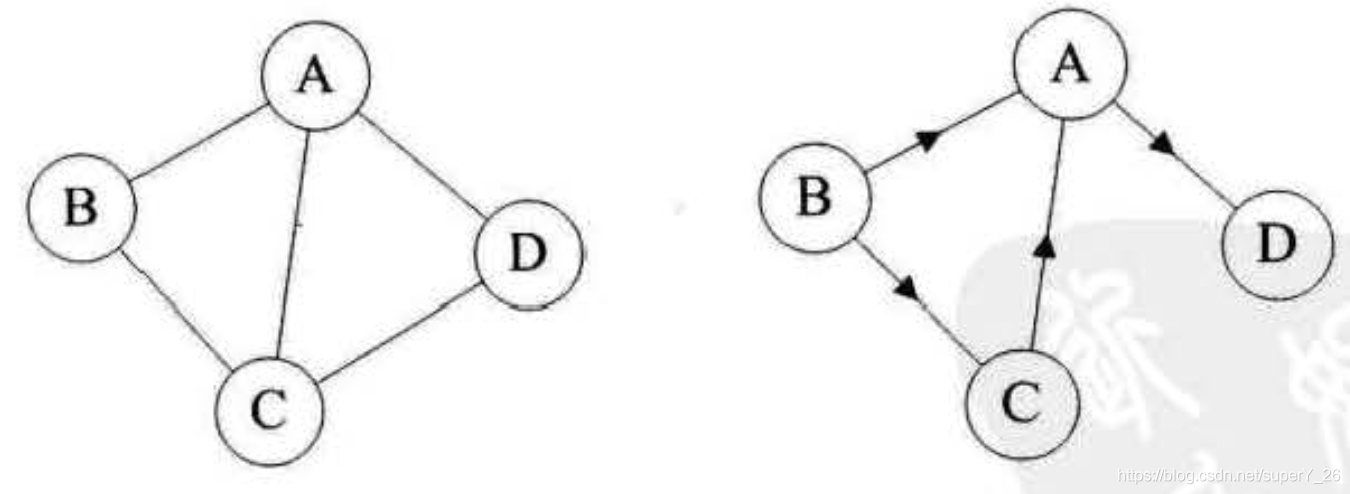
在无向图中,若任意两个顶点之间都存在边,被称为无向完全图,其边的数量为:
n
(
n
?
1
)
2
\frac{n(n-1)}{2}
2n(n?1)?。在有向图中,若任意两个顶点之间都存在两条方向相反的边,被称为有向完全图,其边的数量为
n
(
n
?
1
)
n(n-1)
n(n?1)。
稀疏度,计算公式: e d g e s n o d e s ? ( n o d e s ? 1 ) \frac{edges}{nodes*(nodes-1)} nodes?(nodes?1)edges?,当边很少时,被称为稀疏图,反之,被称为稠密图。
当图中的边带有相应的值,被称为有权图,其值被称为权重
假设两个图:
G
=
(
V
,
E
)
G=(V,E)
G=(V,E)和
G
′
=
(
V
′
,
E
′
)
G'=(V',E')
G′=(V′,E′),其中,
V
′
?
V
V'\sube V
V′?V且
E
′
?
E
E'\sube E
E′?E,则称
G
′
G'
G′为
G
G
G的子图(Subgraph)。如下图:
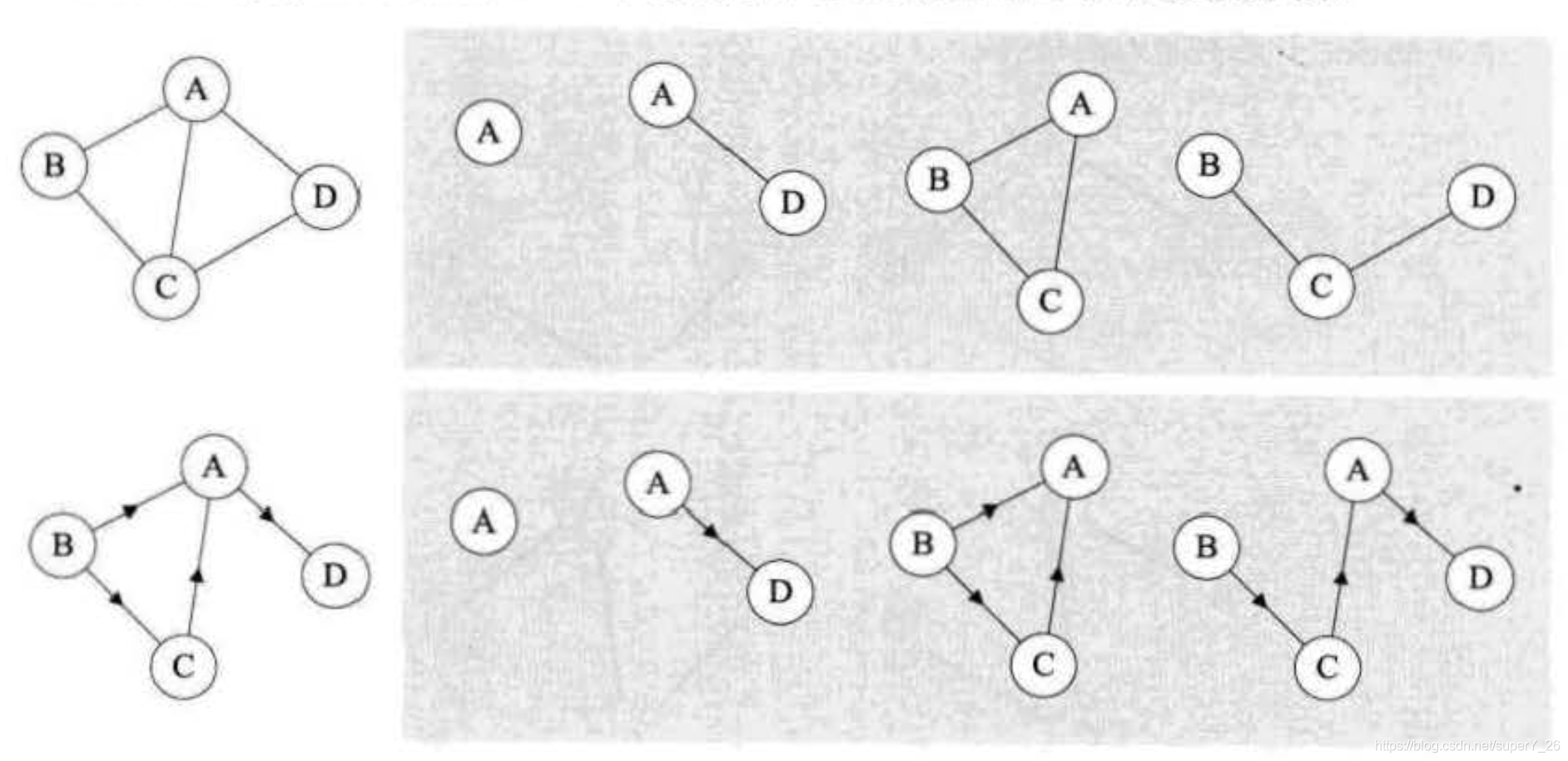
图的度(TD)。有向图有入度(ID)和出度(OD)之分。度为连接顶点 v v v的边的数量。如上图中的顶点 A A A的度为3。有向图中入度为方向指向顶点 v v v的边的数量。出度为从顶点 v v v出发指向其他邻接顶点的边的数量。如上图中顶点 A A A的入度为2,出度为1。
边和度的关系,无向图中, e = 1 2 ∑ i = 1 n T D ( v i ) e=\frac{1}{2}\sum_{i=1}^{n}TD(v_i) e=21?∑i=1n?TD(vi?),有向图中, e = ∑ i = 1 n I D ( v i ) = ∑ i = 1 n O D ( v i ) e=\sum_{i=1}^{n}ID(v_i)=\sum_{i=1}^{n}OD(v_i) e=∑i=1n?ID(vi?)=∑i=1n?OD(vi?)
顶点之间的路径,是顶点 v i v_i vi?到顶点 v j v_j vj?的顶点序列。路径长度是顶点之间边的数量。如上图的无向图中,顶点 B B B到顶点 D D D有4条路径,分别为: ( B , A , D ) , ( B , C , D ) , ( B , A , C , D ) , ( B , C , A , D ) (B,A,D),(B,C,D),(B,A,C,D),(B,C,A,D) (B,A,D),(B,C,D),(B,A,C,D),(B,C,A,D)。有向图中,顶点 B B B到顶点 D D D只有2条路径,分别为: ( B , A , D ) , ( B , C , A , D ) (B,A,D),(B,C,A,D) (B,A,D),(B,C,A,D)。第一个顶点和最后一个顶点相同的路径称为环。
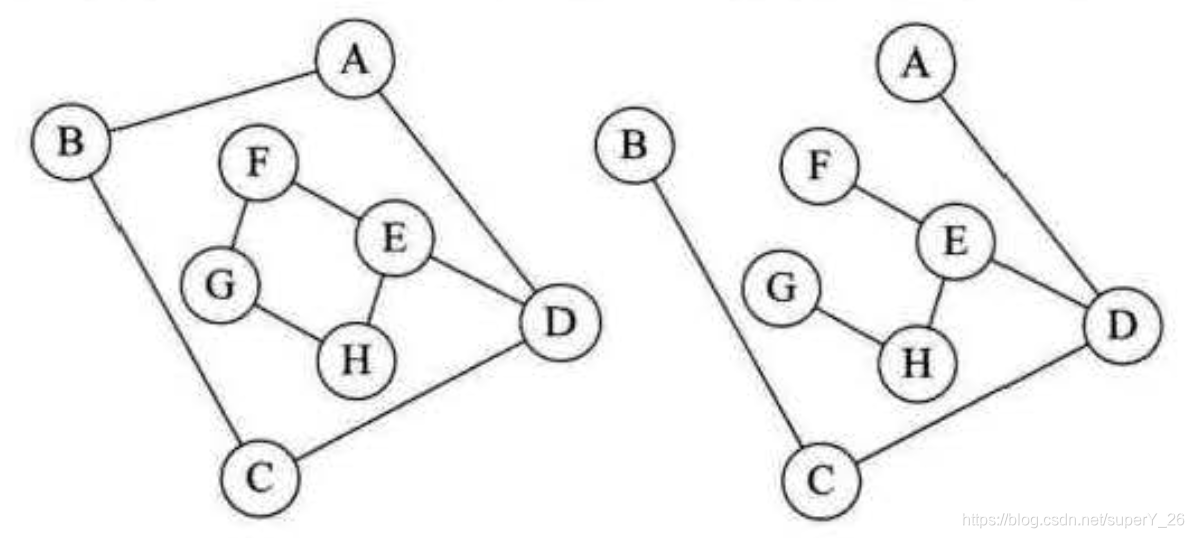
当图中任意两个顶点
v
i
v_i
vi?和
v
j
v_j
vj?都能连通,则称图为连通图。如下图所示左边为非连通图,右边为连通图。
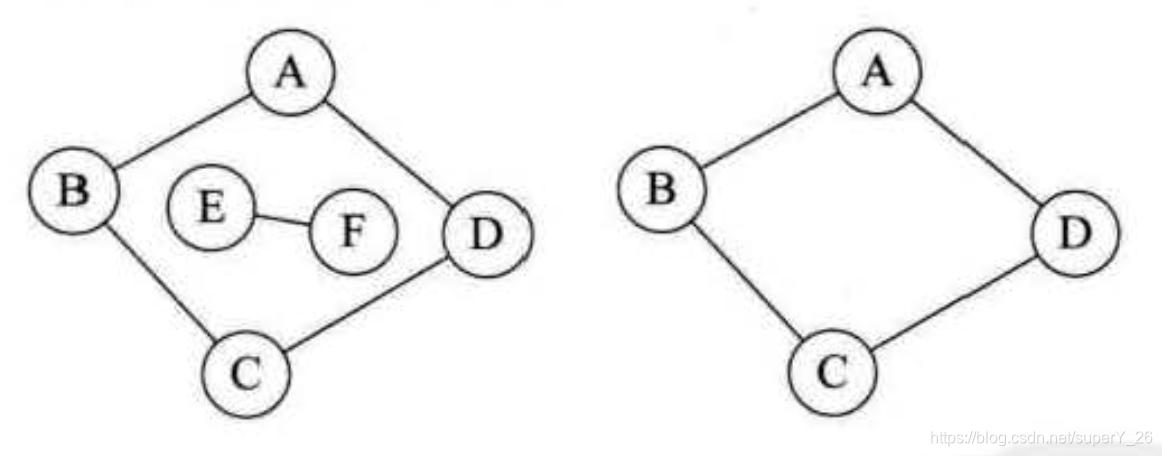
极大连通子图是图中连通顶点数最多的连通图,被称为连通分量。其约束条件为:1、为子图;2、子图是连通图;3、子图再多添加一个顶点就为非连通子图;4、子图中包含了连接这些节点所有的边。如上图中的右边的连通图就是左边图的连通子图。在有向图中,对于每一对顶点,
v
i
,
v
j
∈
V
,
v
i
=?
v
j
v_i,v_j\in V,v_i \not = v_j
vi?,vj?∈V,vi??=vj?,从
v
i
v_i
vi?到
v
j
v_j
vj?和从
v
j
v_j
vj?到
v
i
v_i
vi?都存在路径,则称该有向图为强连通图。有向图的极大强连通子图称为有向图的强连通分量。如下图右边图为左边图的强连通分量。
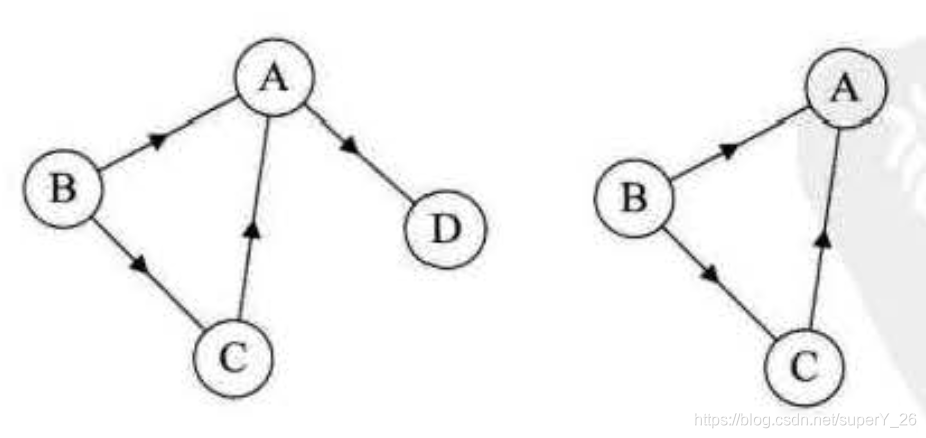
一个连通图的生成树是一个极小的连通子图,它含有图中全部的
n
n
n个顶点,但只有足以构成一课树的
n
?
1
n-1
n?1条边。如下图右图是左图的一个生成树。
图的抽象数据类型和存储
1、 图的邻接矩阵存储方式
设图
G
G
G有
n
n
n个顶点,则邻接矩阵是一个
n
×
n
n \times n
n×n的方阵,定义为:
a
r
c
[
i
]
[
j
]
=
{
1
若
(
v
i
,
v
j
)
∈
E
或
<
v
i
,
v
j
>
∈
E
0
反之?
arc[i][j]=\begin{cases} 1 & 若(v_i,v_j) \in E或 <v_i,v_j> \in E\\ 0 &\text{反之 } \end{cases}
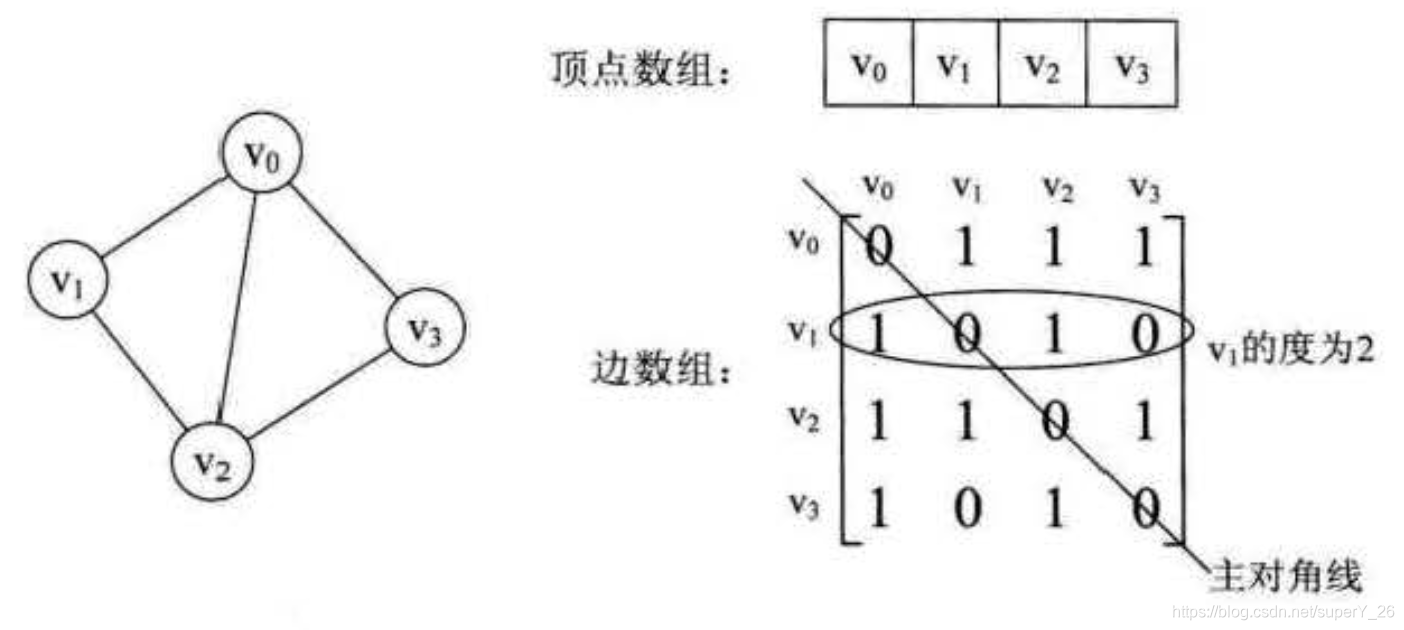
arc[i][j]={10?若(vi?,vj?)∈E或<vi?,vj?>∈E反之??该方式存储有两个数组,一个一维数组,用来存储顶点信息,一个二维数组用来存储边信息。如下图为无向图的存储。
v
e
c
t
e
r
=
[
v
1
,
v
2
,
v
3
,
v
4
]
,
a
r
c
=
[
0
,
1
,
1
,
1
1
,
0
,
1
,
0
1
,
1
,
0
,
1
1
,
0
,
1
,
0
]
vecter=[v_1,v_2,v_3,v_4],arc=\begin{bmatrix} 0,1,1,1 \\ 1,0,1,0 \\ 1,1,0,1 \\ 1,0,1,0 \end{bmatrix}
vecter=[v1?,v2?,v3?,v4?],arc=?????0,1,1,11,0,1,01,1,0,11,0,1,0??????
无向图的边信息矩阵为对称矩阵。 a r c [ 0 ] [ 1 ] = a r c [ 1 ] [ 0 ] = 1 arc[0][1]=arc[1][0]=1 arc[0][1]=arc[1][0]=1表示顶点 v 0 v_0 v0?到顶点 v 1 v_1 v1?存在一条边。有了这个矩阵就可以清楚的知道了图的边信息:
- 可以直接判断任意两个顶点是否有无边了,如顶点 v 1 v_1 v1?和顶点 v 2 v_2 v2?之间是否存在边就是 a r c [ 1 ] [ 2 ] = 1 arc[1][2]=1 arc[1][2]=1。
- 可以知道某个顶点的度,如顶点 v 2 v_2 v2?的度为 a r c [ 2 ] = [ 1 , 1 , 0 , 1 ] arc[2]=[1,1,0,1] arc[2]=[1,1,0,1]数组的和,即 1 + 1 + 0 + 1 = 3 1+1+0+1=3 1+1+0+1=3。
- 可以知道任意某个顶点的邻接顶点,如顶点 v 2 v_2 v2?的邻接顶点为 a r c [ 2 ] = [ 1 , 1 , 0 , 1 ] arc[2]=[1,1,0,1] arc[2]=[1,1,0,1]数组的元素不为零对应的顶点,即 v 0 , v 1 , v 3 v_0,v_1,v_3 v0?,v1?,v3?
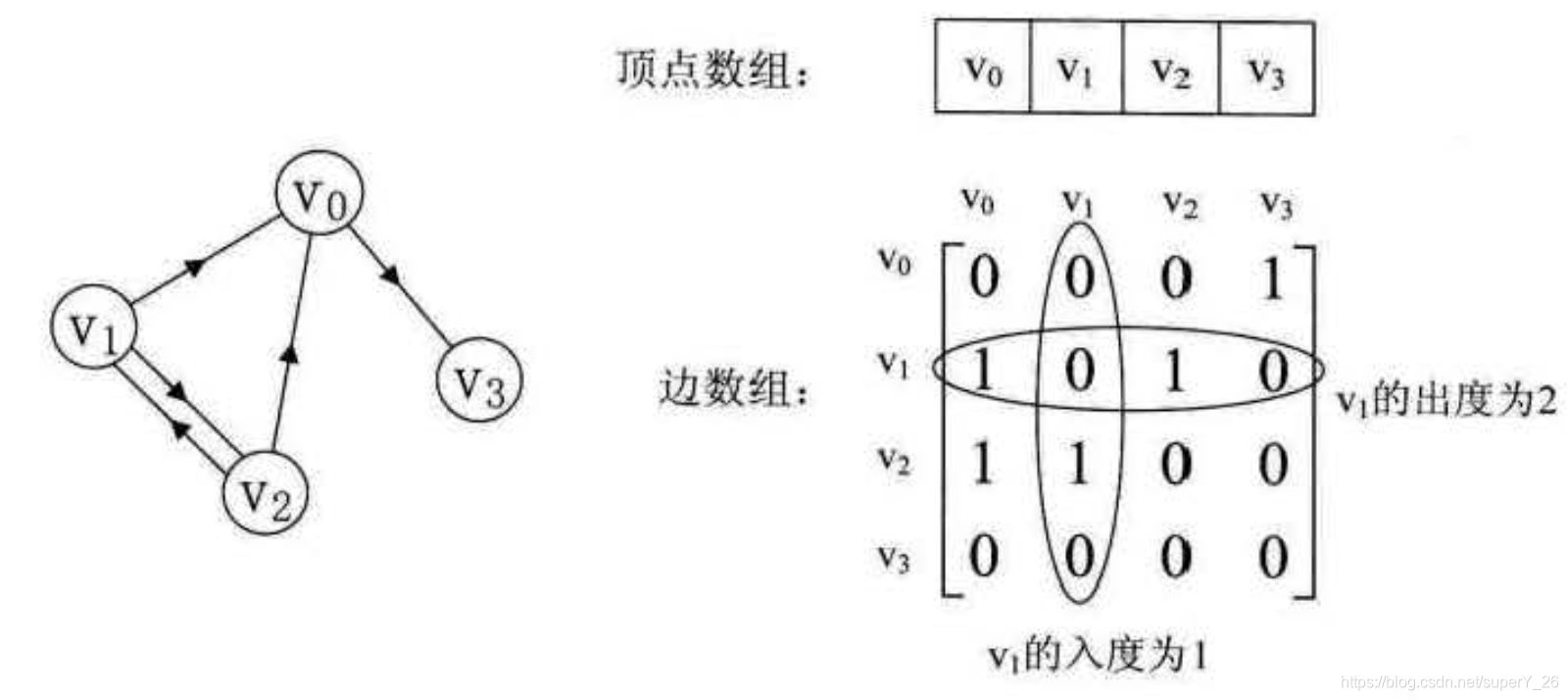
有向图,边信息的二维矩阵不是对称,因为边有方向,如下图所示:
v
e
c
t
e
r
=
[
v
1
,
v
2
,
v
3
,
v
4
]
,
a
r
c
=
[
0
,
0
,
0
,
1
1
,
0
,
1
,
0
1
,
1
,
0
,
0
0
,
0
,
0
,
0
]
vecter=[v_1,v_2,v_3,v_4],arc=\begin{bmatrix} 0,0,0,1 \\ 1,0,1,0 \\ 1,1,0,0 \\ 0,0,0,0 \end{bmatrix}
vecter=[v1?,v2?,v3?,v4?],arc=?????0,0,0,11,0,1,01,1,0,00,0,0,0??????
有向图的度分为入度和出度,如上图二维数组的列为顶点的入度,行为顶点的出度。
带权图的表示:
a
r
c
[
i
]
[
j
]
=
{
w
i
j
若
(
v
i
,
v
j
)
∈
E
或
<
v
i
,
v
j
>
∈
E
0
若
i
=
j
∞
反
之
arc[i][j]=\begin{cases} w_{ij} & 若(v_i,v_j) \in E或 <v_i,v_j> \in E\\ 0 & 若 i = j \\ \infty & 反之 \end{cases}
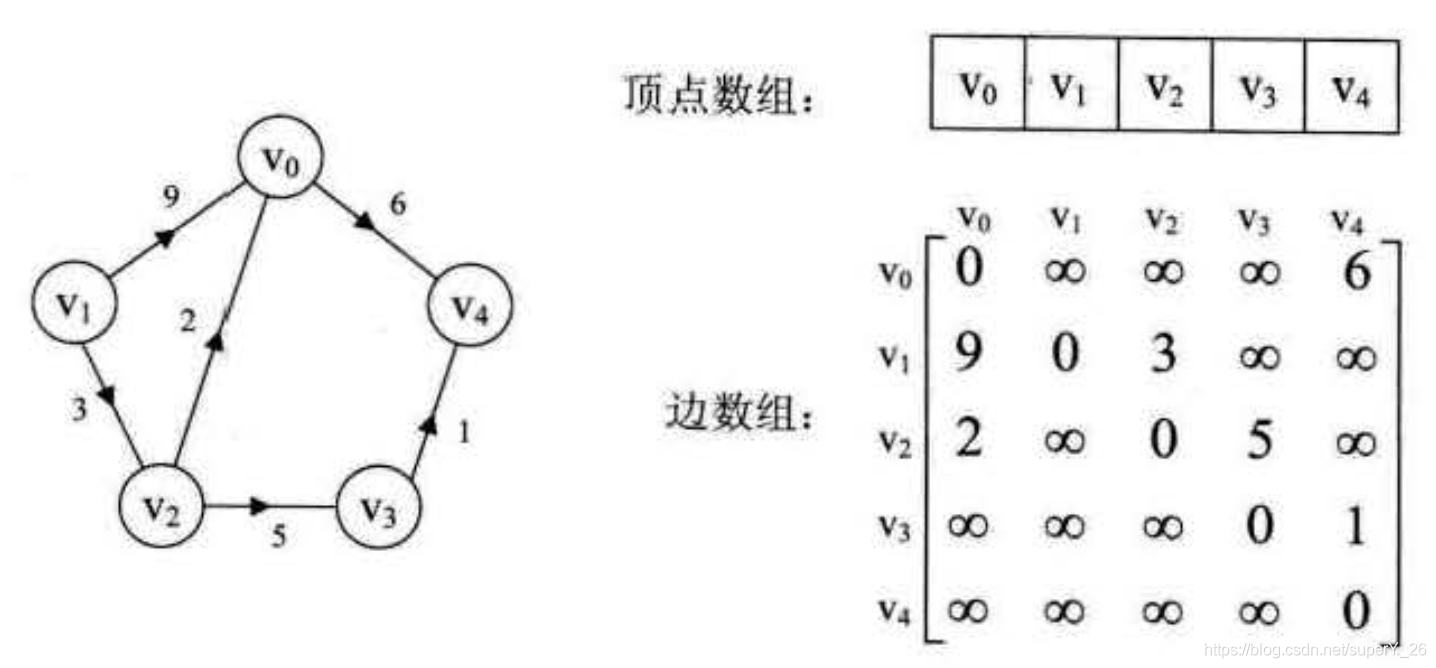
arc[i][j]=??????wij?0∞?若(vi?,vj?)∈E或<vi?,vj?>∈E若i=j反之?其中
w
[
i
j
]
w_[ij]
w[?ij]表示顶点
v
i
v_i
vi?和顶点
v
j
v_j
vj?之间边的权重。如下图有向带权图。
图的算法描述:
class graph:
def __init__(self, vector=None, edges=None)
# vector information
self.vector = vector
# edges information 2 dimension array
self.edges = edges
其中包含顶点信息的一维数组,以及包含边信息的二维数组。
2、 图的邻接表存储方式
邻接矩阵的存储方式对稀疏图非常不友好,存在存储空间的极大浪费。
邻接表的存储原理:
- 顶点用一个一维数组存储。
- 每个顶点的所有邻接顶点使用一个单链表存储,对于有向图,其也是有方向的。
如下图所示,顶点
v
0
v_0
v0?的邻接顶点有
v
1
,
v
2
,
v
3
v_1,v_2,v_3
v1?,v2?,v3?,顶点
v
1
v_1
v1?的邻接顶点有
v
0
,
v
2
v_0,v_2
v0?,v2?,顶点
v
2
v_2
v2?的邻接顶点有
v
0
,
v
1
,
v
3
v_0,v_1,v_3
v0?,v1?,v3?,顶点
v
3
v_3
v3?的邻接顶点有
v
0
,
v
2
v_0,v_2
v0?,v2?。
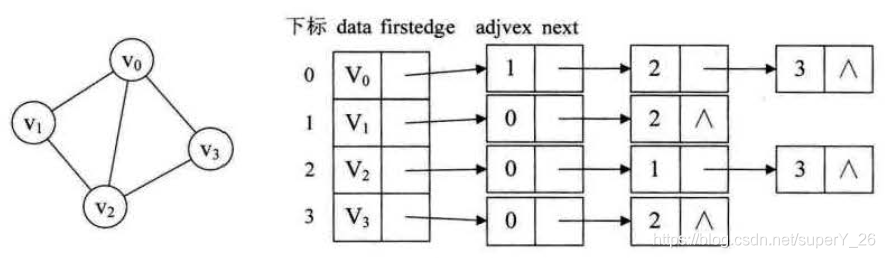
这样的结构我们也可以轻松的图的相关信息:
- 顶点信息从数组中获取
- 顶点的边信息从对应顶点的链表中获取
有向图则如下所示,因此边是有方向的,所有需要两个链表(邻接表和逆邻接表)来存储信息,邻接链表记录的是当前顶点的出度信息。逆邻接链表记录的是当前顶点的入度信息。
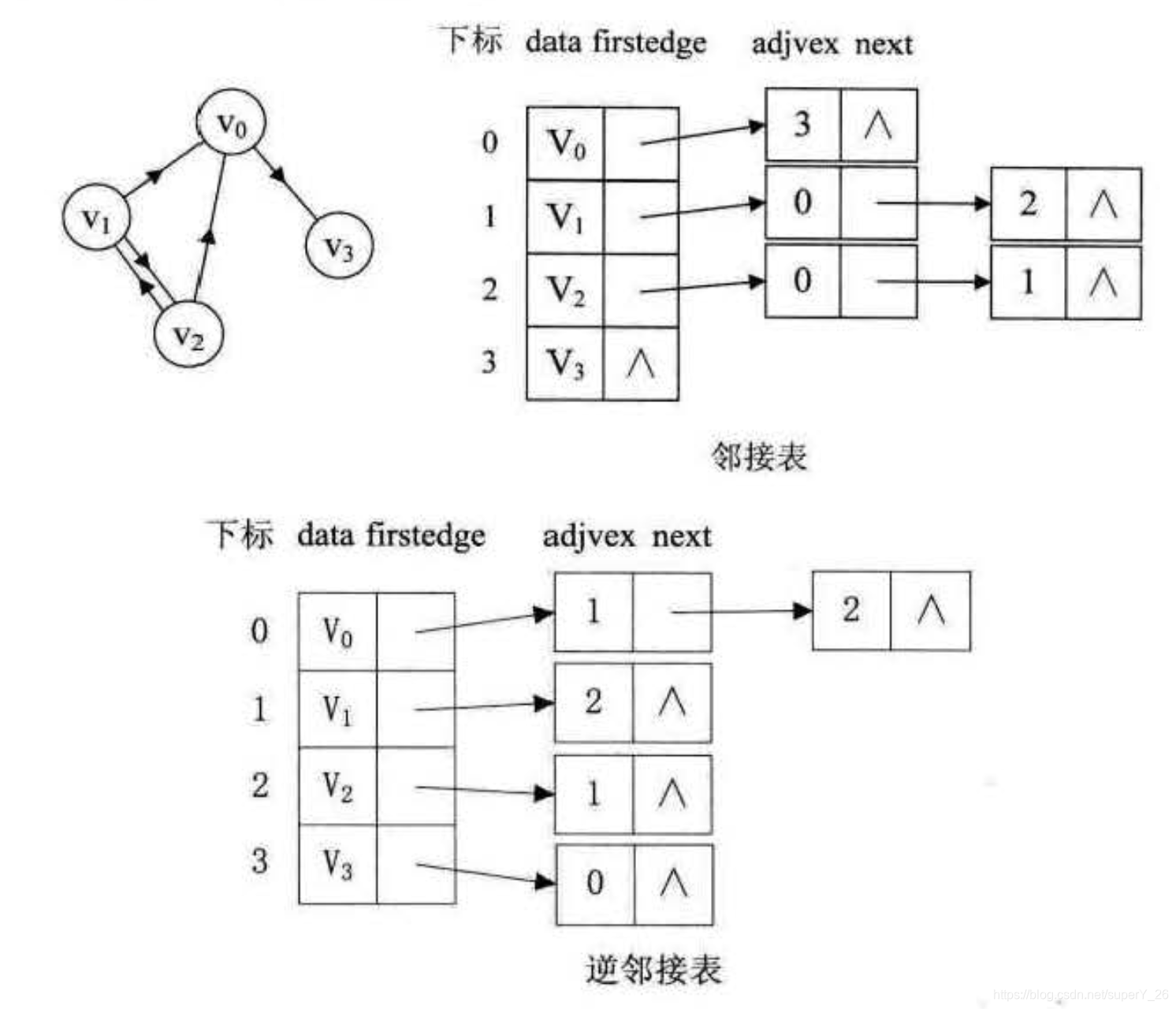
对于带权图来说,就是在链表的节点中再加入一个权重的属性,如下图:
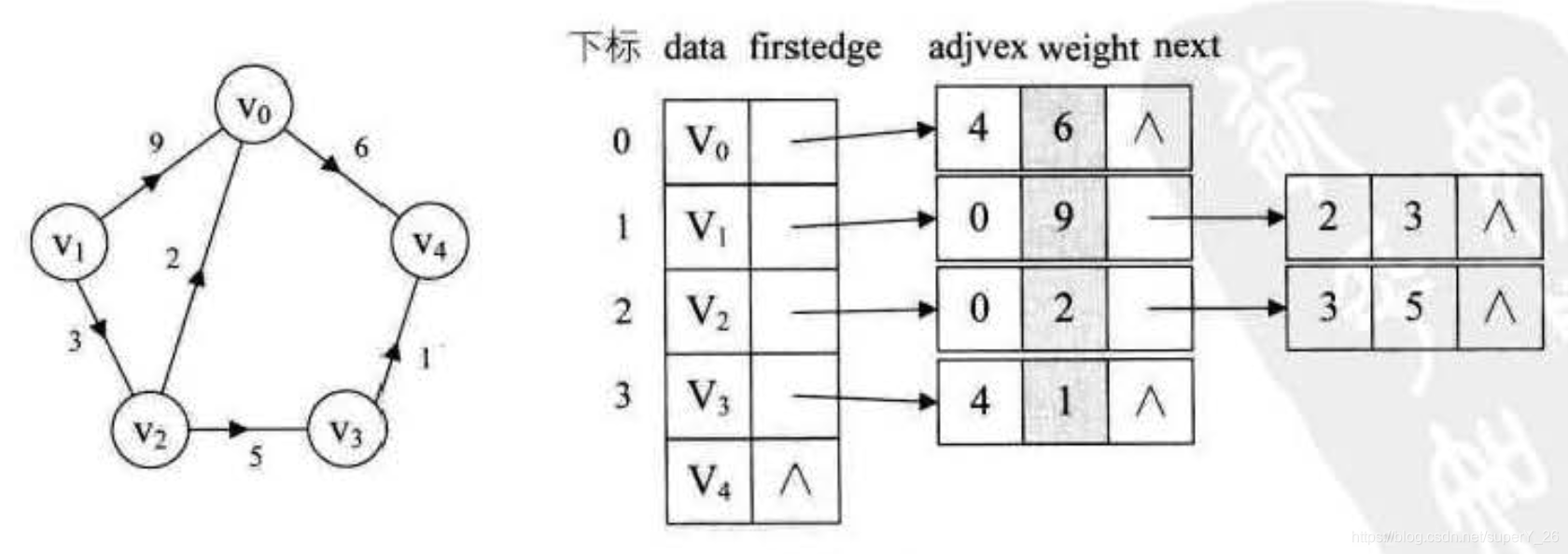
图的算法描述:
# 边信息的链表节点定义
class LinkedNode:
def __init__(self, vector=None, weight=None, next=None):
self.vector = vector
self.weight = weight # 有权图的权重
self.next = next
# 邻接表
class Graph:
def __init__(self, linked=None, reverse_linked=None):
# 数组,数组的每个元素为每个顶点的邻接链表
self.linked = linked
# 数组,数组的每个元素为每个顶点的逆邻接链表 (有向图)
self.reverse_linked = reverse_linked
3、 图的十字链表存储方式
对于有向图来说,邻接链表的存储方式有一定的缺陷,其邻接链表(逆邻接链表)只记录了顶点的出度(入度)。
十字链表存储方式是同时记录顶点的出度和入度的一种存储方式,它将邻接链表和逆邻接链表结合起来。
如下图所示为有向图的十字链表存储方式,其中
f
i
r
s
t
i
n
firstin
firstin表示入边表头指针,指向该顶点的人边表中第一个结点。
f
i
r
s
t
o
u
t
firstout
firstout表示出边表头指针,指向该顶点的出边表中 的 第一个结点。tailvex 是指弧起点在顶点袤的下标, headvex 是指弧终点在顶点表中的下标, headlink 是指入边表指针域,指向终点相同的下一条边, taillink 是指边表指针域,指向起点相同的下一条边。
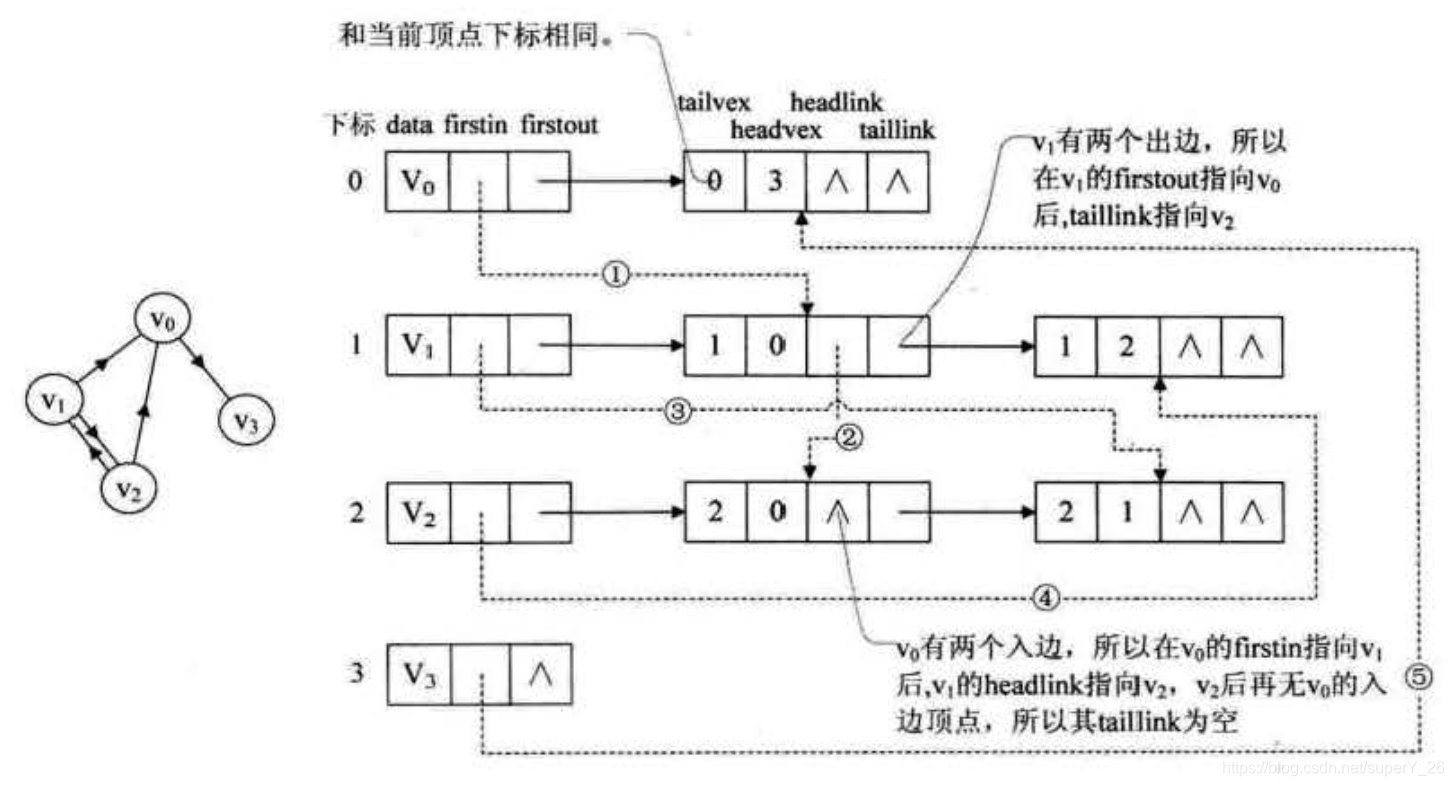
十字链表存储方式可以容易的找到顶点的入度和出度。而它除了结构有点复杂之外,创建图算法的时间复杂度和邻接链表是一样的。因此,在有向图中具有非常好的应用。
4、 图的邻接多重表存储方式
在无向图的邻接链表中,想要关注边的操作,比如对己访问过的边做标记,删除某一条边等操作,那就意味着需要找到这条边的两个边表结点进行操作,这其实还是比较麻烦的。因此,对邻接链表进行的改进,如下图所示。其链表的节点包含四个属性,
i
v
e
x
ivex
ivex和
j
v
e
x
jvex
jvex是与某条边依附的两个顶点在顶点表中下标。
i
l
i
n
k
ilink
ilink指向依附顶点
i
v
e
x
ivex
ivex的下一条边,
j
l
i
n
k
jlink
jlink指向依附顶点
j
v
e
x
jvex
jvex 的下一条边。
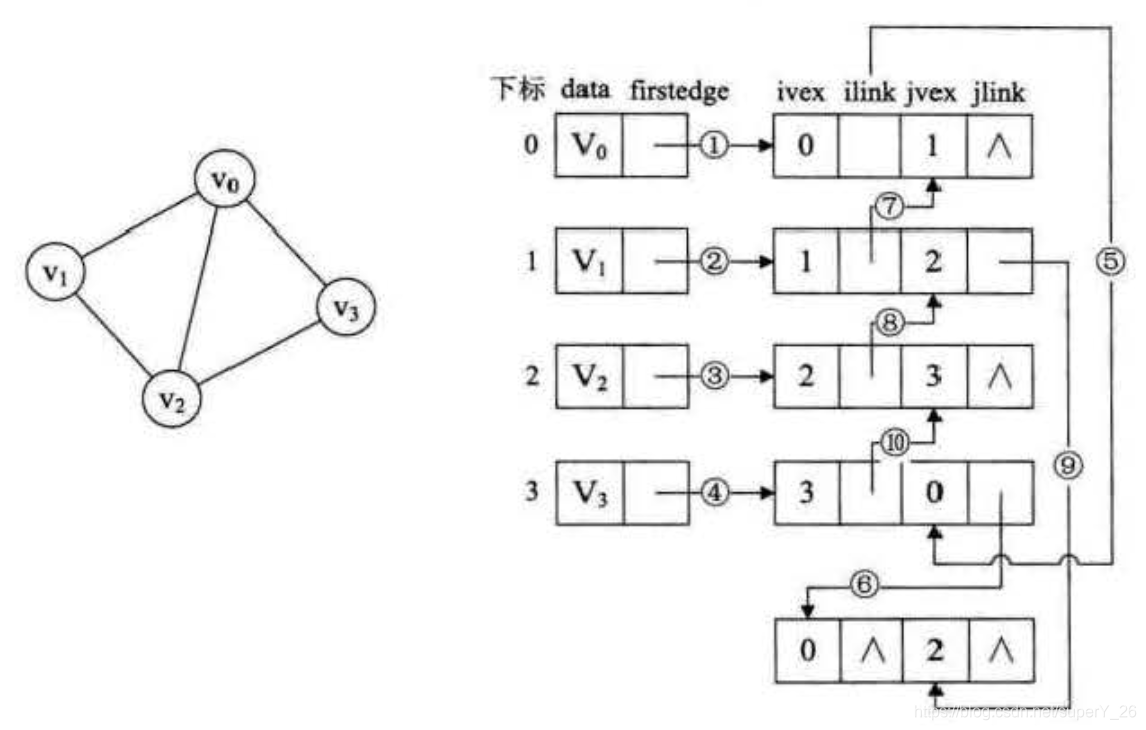
5、 图的边集数组存储方式
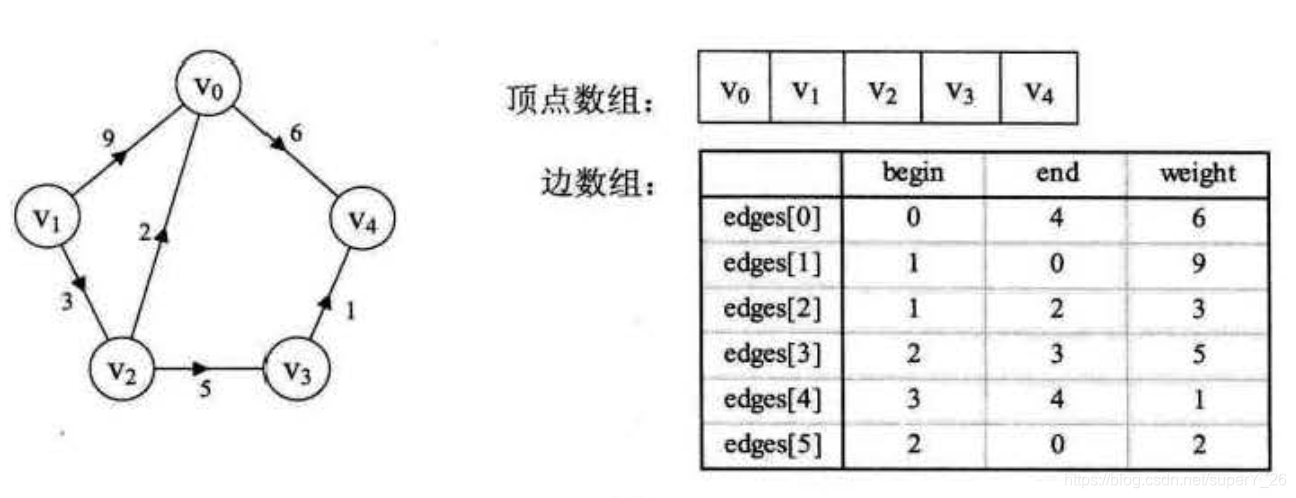
边集数组是由两个一维数组构成。 一个是存储顶点的信息;另一个是存储边的信息,这个边数组每个数据元素由一条边的起点下标 (begin)、终点下标 (end) 和权 (weigbt) 组成。如下图所示。
总结
本文先介绍图结构的相关定义和图的五种存储方式,定义主要有无向(有向)图、顶点、边、出度、入度、图的稀疏度、顶点路径、连通子图。存储结构主要有邻接矩阵、邻接表、十字邻接表、多重邻接表、边集数组。