1. 题目描述

给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你最多可以移动 maxMove 次球。

给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余后的结果。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/out-of-boundary-paths

示例 2：
在这里插入图片描述

输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
输出：12

提示：

1 <= m, n <= 50
0 <= maxMove <= 50
0 <= startRow < m
0 <= startColumn < n

首先认真读题，给定一个矩阵的坐标，在有限步中移动出界的路径数目。根据实例，我们知道访问过的坐标可以再次访问。

那么我们需要记录每个坐标下，在当前最大移动次数下的越界路径数目。

对于每个格子而言，都在上下左右四个方向上都可以移动，最大移动距离为当前的最大移动次数。每次移动后，我们都可以判断是否越界。

那么dp[i][j][k] 表示在坐标为(x,y)的格子在移动次数为k下的越界路径数量。

所以可以用直接上下左右四个方向遍历：

public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
    int[][][] dp = new int[m][n][maxMove + 1];
    // 1. 初始化dp数组
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < n; j++) {
            for (int k = 0; k <= maxMove; k++) {
                dp[i][j][k] = -1;
            }
        }
    }
    return dfs(dp, startRow, startColumn, maxMove, m, n);
}

private int dfs(int[][][] dp, int startRow, int startColumn, int maxMove, int m, int n) {
    if(startColumn < 0 || startRow < 0 || startColumn >= n || startRow >= m) return 1; // 出界
    if(maxMove == 0) return 0; // 达到最小步数
    if(dp[startRow][startColumn][maxMove] != -1) return dp[startRow][startColumn][maxMove];
    int sum = 0;
    sum = (sum + dfs(dp, startRow + 1, startColumn, maxMove - 1, m, n)) % 1000000007;
    sum = (sum + dfs(dp, startRow - 1, startColumn, maxMove - 1, m, n)) % 1000000007;
    sum = (sum + dfs(dp, startRow, startColumn + 1, maxMove - 1, m, n)) % 1000000007;
    sum = (sum + dfs(dp, startRow, startColumn - 1, maxMove - 1, m, n)) % 1000000007;

    // 记录当前值
    dp[startRow][startColumn][maxMove] = sum;
    return sum;
}

这个搜索过程可以使用动态规划来求解。如上所述：dp[i][j][k] 表示在坐标为(x,y)的格子在移动次数为k下的越界路径数量。

那么，在上面搜索过程中，每个位置的值都来源于周围四个格子的累加，即：

dp[i][j][k] = dp[i-1][j][k-1] + dp[i+1][j][k-1] + dp[i][j-1][k-1] + dp[i][j+1][k-1];

比如，最大移动次数为1的时候：
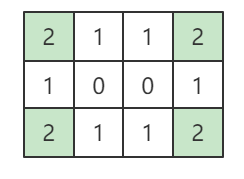
在这里插入图片描述
可以看出，我么可以将四个边缘初始化为1，然后做累加操作，即可得到。

public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {
    int[][][] dp = new int[m][n][maxMove + 1];
    int[][] dirs = new int[][] {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
    // 1. 初始化dp数组
    for (int k = 1; k <= maxMove; k++) {
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
            	// 如果一步可以越界，就累加1，上下左右四个方向都要判断
                if(i == 0) dp[i][j][k]++;
                if(j == 0) dp[i][j][k]++;
                if(i == m - 1) dp[i][j][k]++;
                if(j == n - 1) dp[i][j][k]++;

                int sum = dp[i][j][k];
                for (int[] dir : dirs) {
                    int next_i = i + dir[0];
                    int next_j = j + dir[1];
                    if(next_i >= 0 && next_i < m && next_j >= 0 && next_j < n){
                        sum = (sum + dp[next_i][next_j][k - 1]) % 1000000007;
                    }
                }
                dp[i][j][k] = sum;
            }
        }
    }
    return dp[startRow][startColumn][maxMove];
}