[数据结构与算法]LC295. 数据流的中位数

295. 数据流的中位数
中位数是有序列表中间的数。如果列表长度是偶数，中位数则是中间两个数的平均值。
例如，
[2,3,4] 的中位数是 3
[2,3] 的中位数是 (2 + 3) / 2 = 2.5

设计一个支持以下两种操作的数据结构：
void addNum(int num) - 从数据流中添加一个整数到数据结构中。
double findMedian() - 返回目前所有元素的中位数。

示例：

addNum(1)
addNum(2)
findMedian() -> 1.5
addNum(3) 
findMedian() -> 2

进阶:
如果数据流中所有整数都在 0 到 100 范围内，你将如何优化你的算法？
如果数据流中 99% 的整数都在 0 到 100 范围内，你将如何优化你的算法？

优先队列（大顶堆+小顶堆）

当从数据流中读出的数的个数为奇数的时候，中位数是「前有序数组」中的最大值，如下左图所示；
当从数据流中读出的数的个数为偶数的时候，左中位数是「前有序数组」中的最大值，右中位数是「后有序数组」中的最小值，如下右图所示。

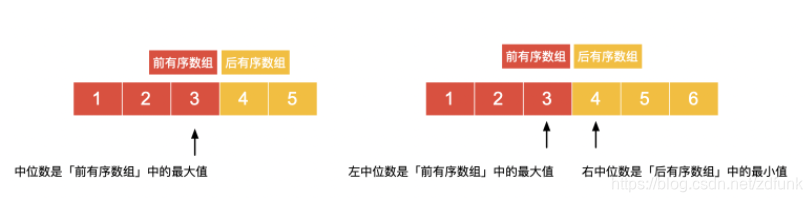
我们只关心这两个 有序数组 中的最值，有一个数据结构可以帮助我们快速找到这个最值，这就是 优先队列 。具体来说：

前有序数组由于只关注最大值，可以 动态地 放置在一个最大堆中；
后有序数组由于只关注最小值，可以 动态地 放置在一个最小堆中。

当从数据流中读出的数的个数为偶数的时候，我们想办法让两个堆中的元素个数相等，两个堆顶元素的平均值就是所求的中位数（如下左图）；

当从数据流中读出的数的个数为奇数的时候，我们想办法让最大堆的元素个数永远比最小堆的元素个数多 1 个，那么最大堆的堆顶元素就是所求的中位数（如下右图）。

Java优先队列：PriorityQueue，默认构造方法是构造小顶堆

        maxheap = new PriorityQueue<>((x, y) -> y - x);//大顶堆
        minheap = new PriorityQueue<>();//小顶堆

import java.util.PriorityQueue;

public class MedianFinder {

    /**
     * 当前大顶堆和小顶堆的元素个数之和
     */
    private int count;
    private PriorityQueue<Integer> maxheap;
    private PriorityQueue<Integer> minheap;

    /**
     * initialize your data structure here.
     */
    public MedianFinder() {
        count = 0;
        maxheap = new PriorityQueue<>((x, y) -> y - x);
        minheap = new PriorityQueue<>();
    }

    public void addNum(int num) {
        count += 1;
        maxheap.offer(num);
        minheap.add(maxheap.poll());
        // 如果两个堆合起来的元素个数是奇数，小顶堆要拿出堆顶元素给大顶堆
        if ((count & 1) != 0) {
            maxheap.add(minheap.poll());
        }
    }

    public double findMedian() {
        if ((count & 1) == 0) {
            // 如果两个堆合起来的元素个数是偶数，数据流的中位数就是各自堆顶元素的平均值
            return (double) (maxheap.peek() + minheap.peek()) / 2;
        } else {
            // 如果两个堆合起来的元素个数是奇数，数据流的中位数大顶堆的堆顶元素
            return (double) maxheap.peek();
        }
    }
}

作者：liweiwei1419
链接：https://leetcode-cn.com/problems/find-median-from-data-stream/solution/you-xian-dui-lie-python-dai-ma-java-dai-ma-by-liwe/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。