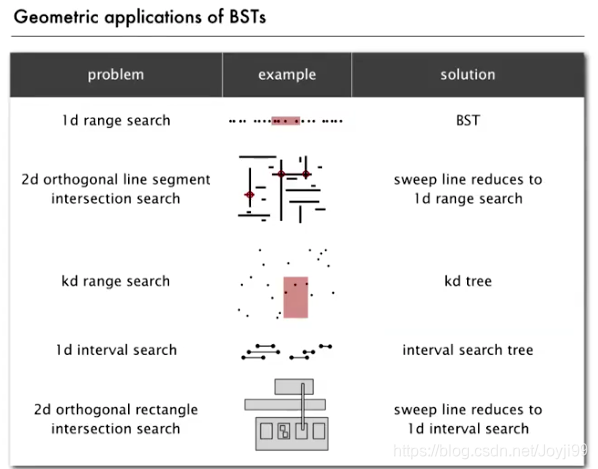
Geometric Applications of BSTs
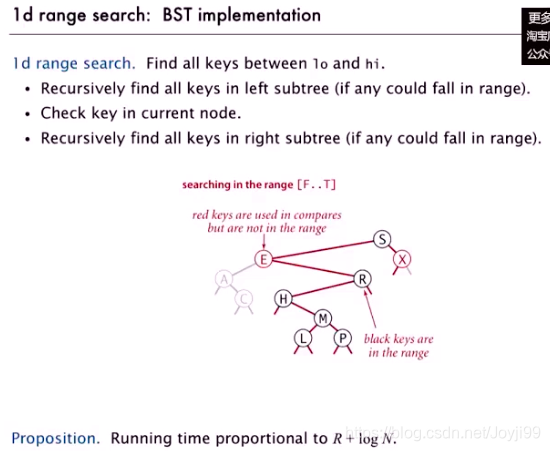
1 1d range search 一维区间搜索



//Returns the number of keys in the symbol table in the given range,两个边界也取进去
public int size(Key lo, Key hi){
if (contains(hi)) return rank(hi) - rank(lo) + 1;
else return rank(hi) - rank(lo);//lo这边的rank始终一样
}
//Does this symbol table contain the given key?
public boolean contains(Key key) {
if (key == null) throw new IllegalArgumentException("argument to contains() is null");
return get(key) != null;
}
public int rank(Key key){
return rank(key, root);
}
private int rank(Key key, Node x){
//返回以x为根结点的子树中小于x.key的键的数量
if (x == null) return 0;
int cmp = key.compareTo(x.key);
if (cmp < 0) return rank(key, x.left);//若key小于根结点,返回key在左子树的排名(递归)
else if (cmp > 0) return 1 + size(x.left) + rank(key, x.right);
else return size(x.left);//如果key和根结点的key相等,rank就是左边子树的结点总数
}
2 line segment intersection 线段交点几何问题
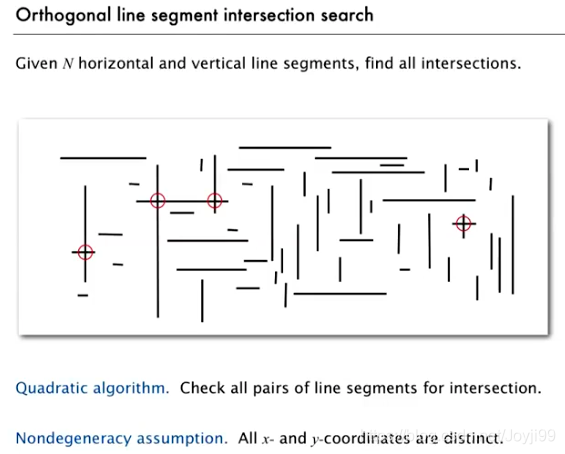
- 扫描线算法
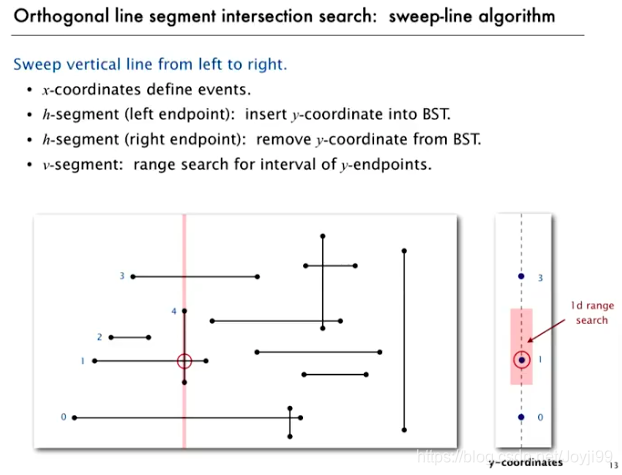

3 kd trees
3.1 2d正交范围搜索
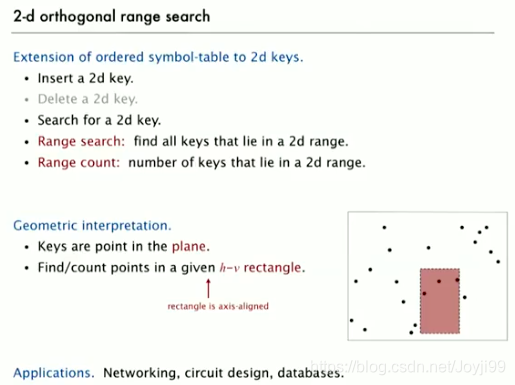
3.3.1 网格分割法
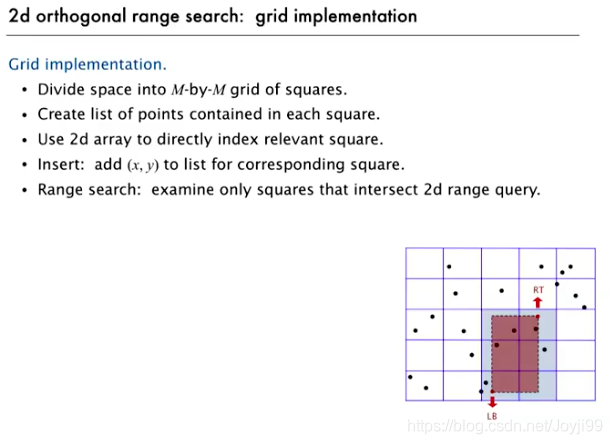
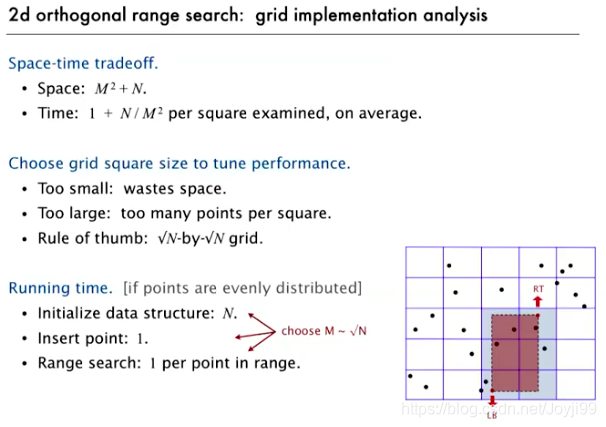
- 选择根号N为M的大小(小正方形边长),可以保证时间不变
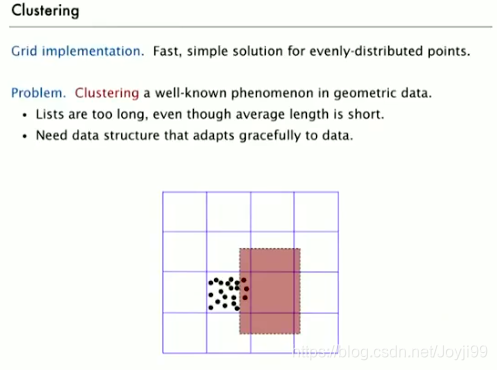
- 因此,针对有些数据不随机的情况,grid implementation并不合适
3.3.2 递归分割法

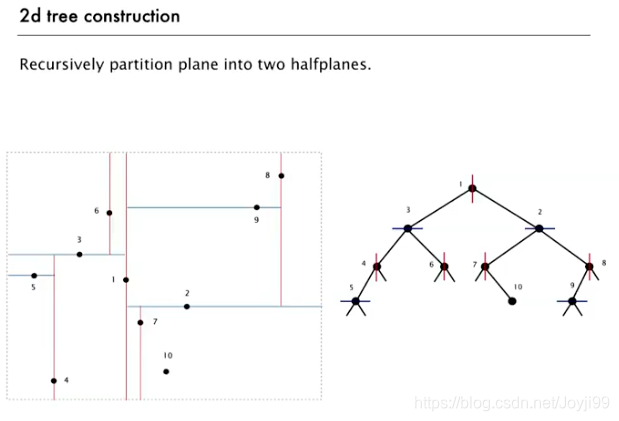
- 下在左,上在右
- 单数用垂线,双数key用水平线
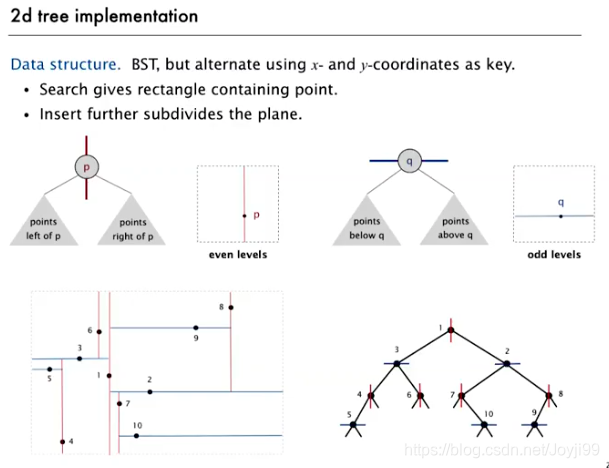
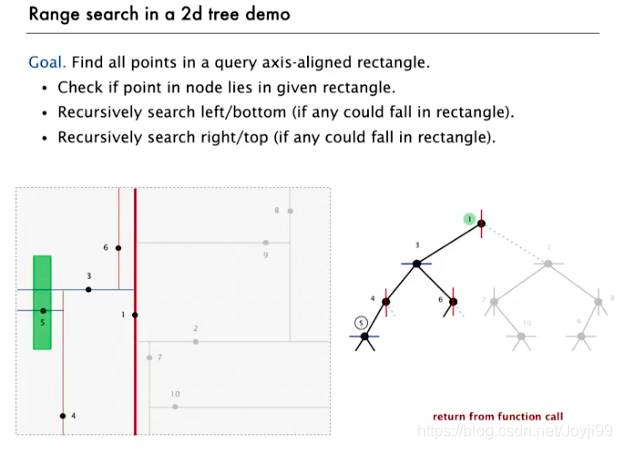
- 如果一条线穿过区域,则左右子树都要遍历,先遍历一边,结束,再另一边
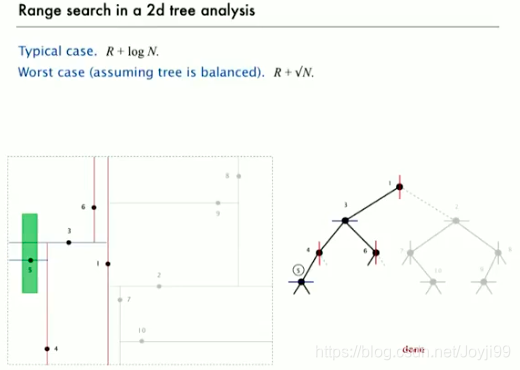
- R是所有要返回的包含在区域内的点
3.2 nearest neighbor search
- 寻找一点周围最近的点
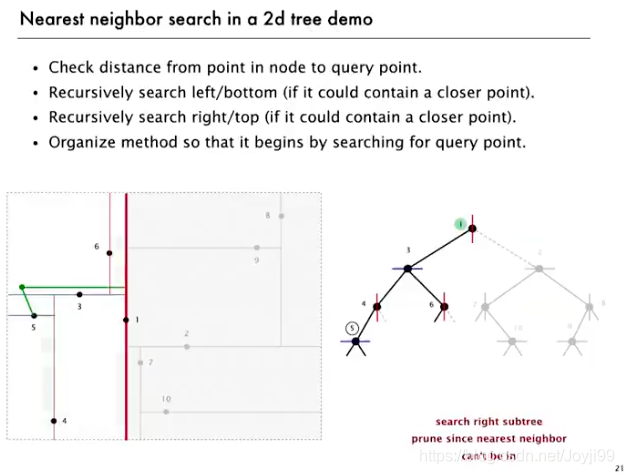
- query point在一点左边,因此先遍历左子树(右子树稍后也要遍历)
- 如果在左子树中,找到距离更小的点,把这个点设为新的champion,且不再遍历右子树,因为比query point到1点所在垂线的垂直距离短
- 上下同理
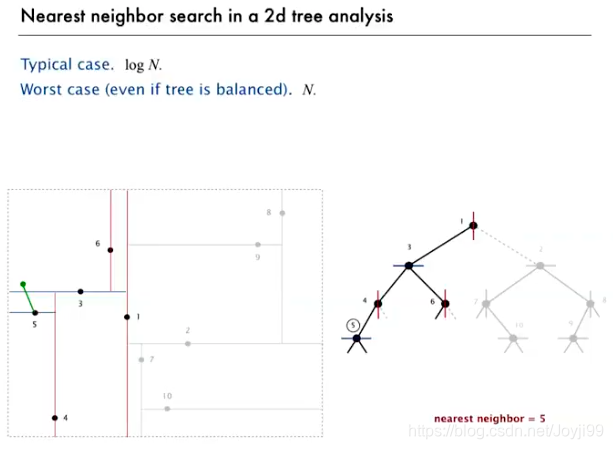
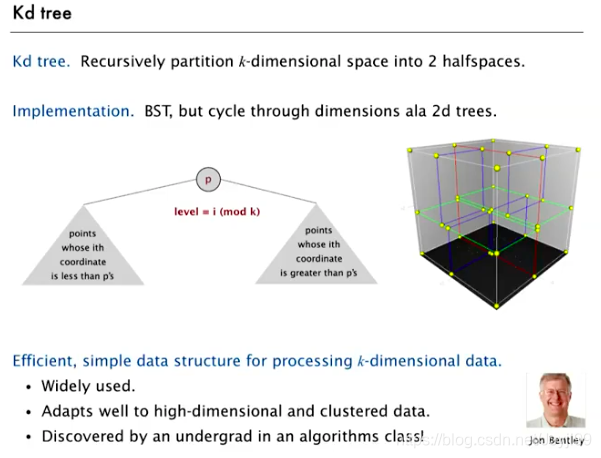
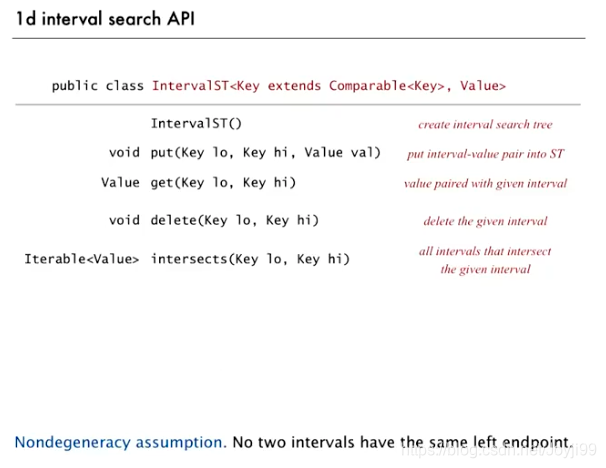
4 interval search trees 区间搜索树

4.1 1d区间搜索
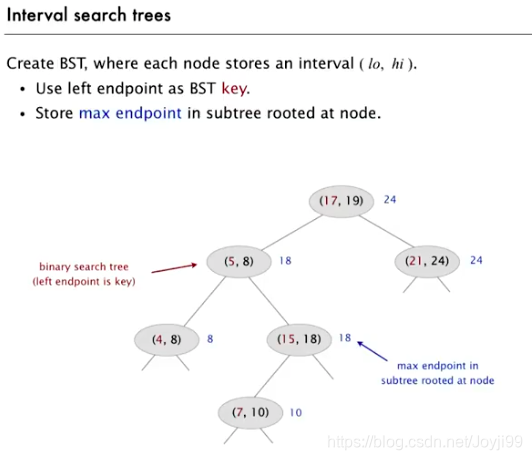
4.1.1 插入
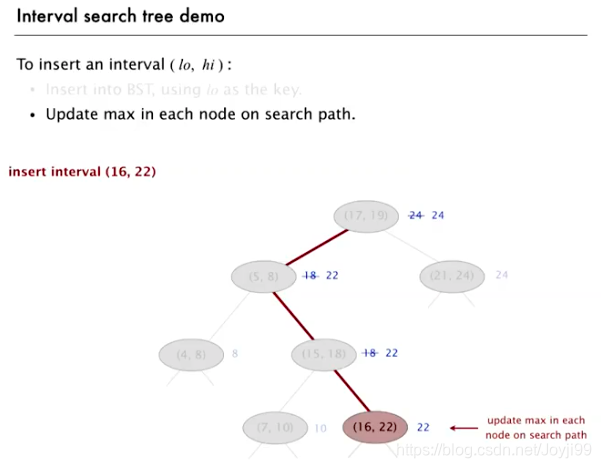
4.1.2 search

- 此处max endpoint被用上


Node x = root;
while (x != null){
if (x.interval.intersects(lo,hi)) return x.interval;
else if (x.left = null) x = x.right;
else if (x.left.max < lo) x = x.right;
else x = x.left;
}
return null;
- 源码见algs4 --> Interval1D



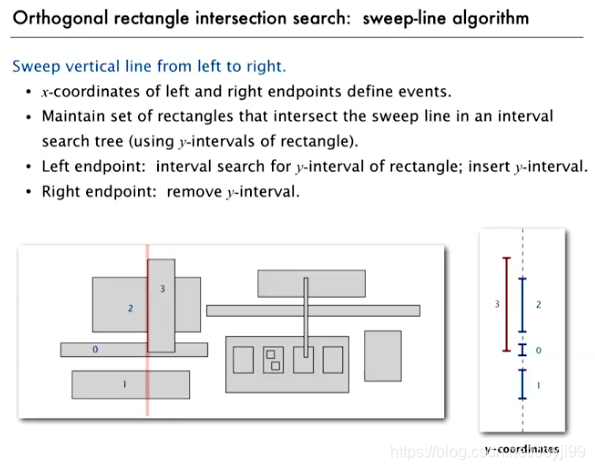
5 rectangle intersection