A

比较简单

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;
int main()
{
	int n;
	cin>>n;
	if(n<126) cout<<4<<'\n';
	else if(n<212) cout<<6<<'\n';
	else cout<<8<<'\n';
	return 0; 
}

B

直接暴力枚举所有情况1e6计算量不会超时

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;

int main()
{
	ll res = 0;
	int s,t;
	cin>>s>>t;
	for(int i=0;i<=100;i++)
		for(int j=0;j<=100;j++)
			for(int k=0;k<=100;k++)
				if(i+j+k<=s&&i*j*k<=t)res ++;
	cout<<res<<'\n';
	return 0; 
}

C

题目中给的是一个环形的问题
注意环形问题一般都需要转换为链状问题进行解决

解决的方法：将环拆成链长度变为2倍，等于把链复制一下加到后面

首先将答案存入 $r e s [i]$ 数组中，第一次得到的时间可能是刚开始被分发的时间

然后用 $m n$ 记录到达第i个人时第一次接到前一个人传宝石的最小时刻（贪心），接到前一个人传递的宝石可能是更前面的人传的
$t t$ 是前一个人得到分发的宝石后向后传的的时间，然后比较 $t t$ 和 $m n$ ，如果 $t t$ 更小的话需要更新 $m n$

每次到达一个人时就维护一下答案

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e5+5;
ll s[N*2],t[N*2],res[N*2];
int n;

int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) 
	{
		cin>>s[i];
		s[i+n] = s[i];
	}
	for(int i=1;i<=n;i++)
	{
		cin>>t[i];
		t[i+n] = t[i];
		res[i] = t[i];
		res[i+n] = res[i];
	}
	ll mn = t[1];
	for(int i=2;i<=n*2;i++)
	{
		mn += s[i-1];
		ll tt = s[i-1] + t[i-1];
		if(tt < mn) mn = tt;
		if(mn < res[i%n==0 ? n : i%n]) res[i%n==0 ? n : i%n] = mn;
	}
	for(int i=1;i<=n;i++) cout<<res[i]<<'\n';
	return 0; 
}

D

题目求的可以转化为求树中所有两两节点之间路径中最大权值边权值的和

思路：可以发现一条边的权值是一条路径中最大的话，那么这条路径产生的贡献就为这条边左边的点个数乘上右边的点个数再乘上权值

那么我们就可以将边按权值进行排序，从小的开始加边，所以每次加的边的权值一定是最大的，然后贡献就是权值乘上一边儿的连接的点个数再乘上另一边儿的点个数（其中的点必须可达才能把个数加上）。

在计算时候需要用并查集维护点之间的可达性关系，初始化一个sz数组记录点的个数，当有新的边加上时，父节点的个数要加上子节点的个数

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e5+5;

ll f[N],sz[N];
int n;
struct edge
{
	int u,v,w;
	bool operator < (const edge &a) const
	{
		return w < a.w;
	}
}e[N];

void init() 
{
	for(int i=1;i<N;i++) 
	{
		f[i] = i;
		sz[i] = 1;
	}
}
ll ask(int x)
{
	return f[x]==x ? x : f[x]=ask(f[x]);
}
int main()
{
	cin>>n;
	for(int i=1;i<n;i++) cin>>e[i].u>>e[i].v>>e[i].w;
	sort(e+1,e+n);
	init();
	ll res = 0;
	for(int i=1;i<n;i++)
	{
		int x = ask(e[i].u),y = ask(e[i].v);
		res += e[i].w * sz[x] * sz[y];
		//结合
		f[x] = y;
		sz[y] += sz[x];
	}
	cout<<res<<'\n';
	return 0;
 }

E

题目:
有n个区间，每个区间可以在任意整数点位置放一个球，一个点只能放一个球，求能否放下n个球

区间覆盖问题，一般都需要贪心，都需要对区间进行排序

本题需要使用到优先队列的数据结构，来实现对区间的右端的大小实现实时的有序的功能

将区间存储到pair数组中，对数组进行排序，会首先按照区间的左端点排序，如果左端点相等的话，再排右端点

首先定义cur表示能够放置球的最小坐标点，每次遍历一个区间，如果cur小于当前的左端点那么更新cur，最小可放置坐标点需要右移。

对于所有左端点相同的区间，把右端点加入到优先队列中

在队列不空和cur小于下一个区间的左端点时的条件下，总是取出最小的右端点判断cur是否小于等于它（是否可以放置小球）否则的话就不能放置。

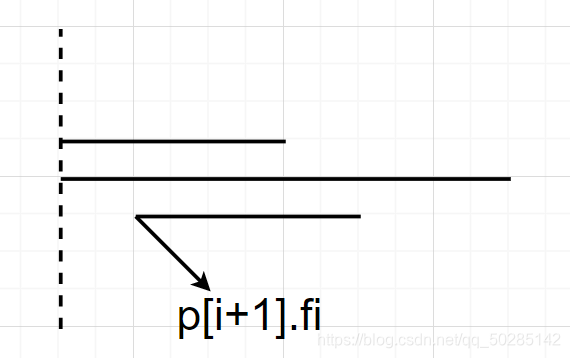
为什么有cur要小于下一个区间的左端点的条件呢？
我们要优先考虑放置先开始的早结束的区间，因为之前的区间先开始我们就把他们加入到队列中，如果当前的所有开头相同的区间还没结束，后一个区间就开始了，肯定时优先放置后面的区间的。这时候循环就要结束，下一个循环就会开始（队列可能没有空），下面继续操作，一直是默认先放小的点
在这里插入图片描述

#include<bits/stdc++.h>
#define fi first
#define se second 
using namespace std;
typedef long long ll;
typedef pair<int ,int> pii;
const int N = 2e5+5;

pii p[N];

void solve()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>p[i].fi>>p[i].se;
	sort(p+1,p+1+n);
	int cur = 0;
	bool is = true;
	p[n+1].fi = 2e9;
	priority_queue<int,vector<int>,greater<int> >pq;
	for(int i=1;i<=n;i++)
	{
		if(cur < p[i].fi) cur = p[i].fi;
		pq.push(p[i].se);
		while(p[i].fi==p[i+1].fi) 
		{
			pq.push(p[i+1].se);
			i++;
		}
		while(!pq.empty()&&cur<p[i+1].fi)
		{
			int t = pq.top();
			pq.pop();
			if(cur <= t) cur++;
			else 
			{
				is = false;
				break;
			}
		}
		if(!is) break;
	}
	if(is) cout<<"Yes\n";
	else cout<<"No\n";
}
int main()
{
	ios::sync_with_stdio(false);
	cin.tie(0),cout.tie(0);
	int _;
	cin>>_;
	while(_--)
	{
		solve();
	}
	return 0;
 }