给定一棵树的前序遍历?
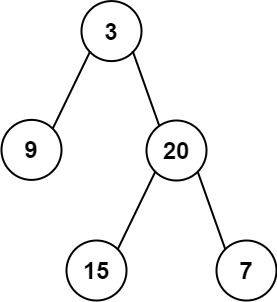
preorder?与中序遍历??inorder。请构造二叉树并返回其根节点。
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:Input: preorder = [-1], inorder = [-1]
Output: [-1]来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
?递归:思路就是我们可以通过前序遍历知道,前序遍历结果数组的第一个元素就是根节点,我们知道这个根节点的值找到它在中序遍历中对应的位置就可以将树分开。
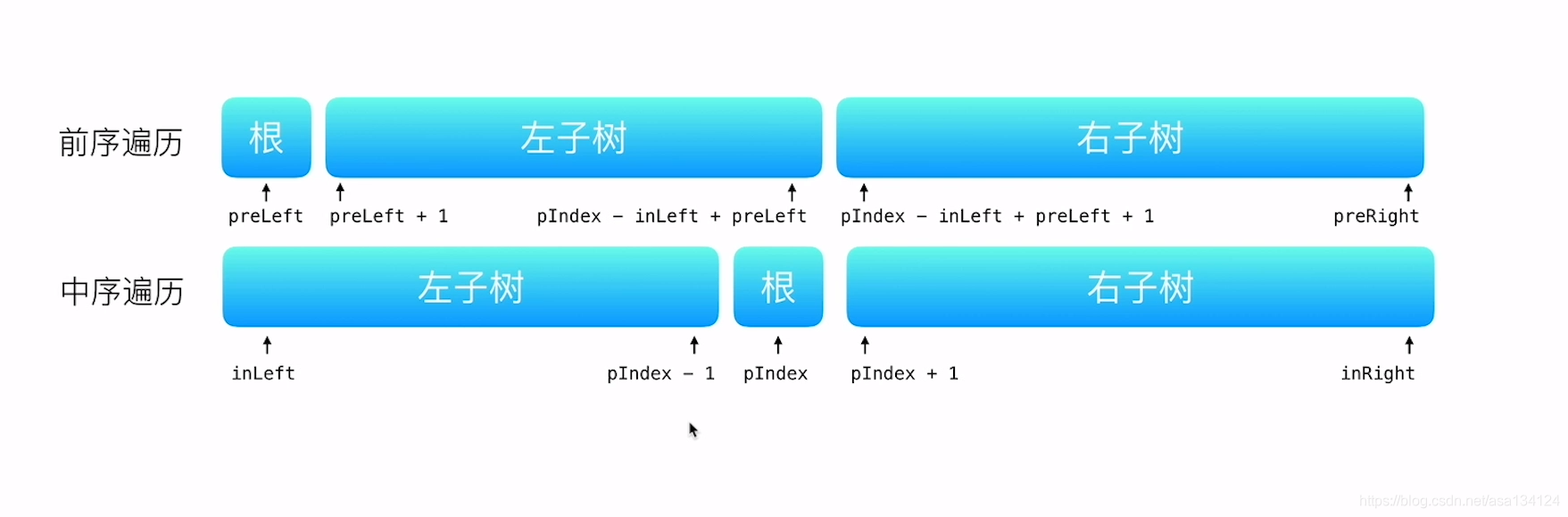
?分出左子树,右字树可以通过同样的方法递归,继续分解,终止条件是preleft>preright,inleft>inright.
?
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
int prelen=preorder.length;
int inlen=inorder.length;
/* if(prelen!=inlen){
return 0;
}*/
Map <Integer,Integer> map=new HashMap<>(prelen);
for(int i=0;i<inlen;i++){
map.put(inorder[i],i);
}
return buildTree(preorder,0,prelen-1,map,0,inlen-1);
}
private TreeNode buildTree(int[] preorder,int preleft,int preright,Map<Integer,Integer>map,int inleft,int inright)
{
if(preleft>preright || inleft>inright){
return null;
}
int rootval=preorder[preleft];
TreeNode root=new TreeNode(rootval);
int pindex=map.get(root.val);
root.left=buildTree(preorder,preleft+1,pindex-inleft+preleft,map,inleft,pindex-1);
root.right=buildTree(preorder,pindex-inleft+preleft+1,preright,map,pindex+1,inright);
return root;
}
}class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder==null||preorder.length==0){
return null;
}
TreeNode root=new TreeNode(preorder[0]);
Deque<TreeNode> stack=new LinkedList<>();
stack.push(root);//存入根节点
int inorderIndex=0;
for(int i=1;i<preorder.length;i++){
int preorderVal=preorder[i];//取出前序遍历数组当前值,便于让其放入节点
TreeNode node=stack.peek();//得到栈顶节点
if(node.val!=inorder[inorderIndex]){//如果栈顶节点不等于中序遍历出的index值,这说明
//它一直是左节点
node.left=new TreeNode(preorderVal);//构造树
stack.push(node.left);//一直将这个节点压入栈中
}else{//当节点与index值相等时,这是说明到了叶子节点
while(!stack.isEmpty()&&stack.peek().val==inorder[inorderIndex]){
node=stack.pop();//取出栈顶元素
inorderIndex++;//index值加加,继续判断是否相等
}
node.right=new TreeNode(preorderVal);//不相等的话,这说明找到右节点的母亲。就是
//最后一个pop出来的节点
stack.push(node.right);//将右节点入栈,继续判断是否是叶子节点
}
}
return root;
}
}方法二:迭代
思路迭代法是一种非常巧妙的实现方法。
对于前序遍历中的任意两个连续节点 u?和 v,根据前序遍历的流程,我们可以知道 u?和 v?只有两种可能的关系:
v?是 u?的左儿子。这是因为在遍历到 u?之后,下一个遍历的节点就是 u?的左儿子,即 v;
u?没有左儿子,并且 v?是 u?的某个祖先节点(或者 u 本身)的右儿子。如果 u?没有左儿子,那么下一个遍历的节点就是 u?的右儿子。如果 u?没有右儿子,我们就会向上回溯,直到遇到第一个有右儿子(且 u 不在它的右儿子的子树中)的节点 u_a,那么 v?就是 u_a?的右儿子。
第二种关系看上去有些复杂。我们举一个例子来说明其正确性,并在例子中给出我们的迭代算法。
例子
我们以树
? ? ? ? 3
? ? ? ?/ \
? ? ? 9 ?20
? ? ?/ ?/ ?\
? ? 8 ?15 ? 7
? ?/ \
? 5 ?10
?/
4
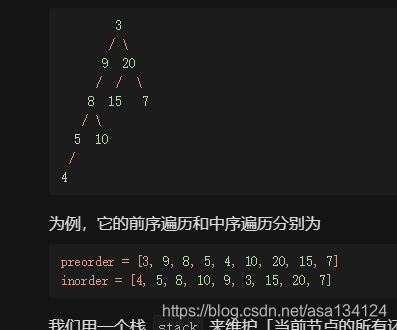
为例,它的前序遍历和中序遍历分别为
preorder = [3, 9, 8, 5, 4, 10, 20, 15, 7]
inorder = [4, 5, 8, 10, 9, 3, 15, 20, 7]
我们用一个栈 stack 来维护「当前节点的所有还没有考虑过右儿子的祖先节点」,栈顶就是当前节点。也就是说,只有在栈中的节点才可能连接一个新的右儿子。同时,我们用一个指针 index 指向中序遍历的某个位置,初始值为 0。index 对应的节点是「当前节点不断往左走达到的最终节点」,这也是符合中序遍历的,它的作用在下面的过程中会有所体现。首先我们将根节点 3 入栈,再初始化 index 所指向的节点为 4,随后对于前序遍历中的每个节点,我们依次判断它是栈顶节点的左儿子,还是栈中某个节点的右儿子。
我们遍历 9。9 一定是栈顶节点 3 的左儿子。我们使用反证法,假设 9 是 3 的右儿子,那么 3 没有左儿子,index 应该恰好指向 3,但实际上为 4,因此产生了矛盾。所以我们将 9 作为 3 的左儿子,并将 9 入栈。
stack = [3, 9]
index -> inorder[0] = 4
我们遍历 8,5 和 4。同理可得它们都是上一个节点(栈顶节点)的左儿子,所以它们会依次入栈。stack = [3, 9, 8, 5, 4]
index -> inorder[0] = 4
我们遍历 10,这时情况就不一样了。我们发现 index 恰好指向当前的栈顶节点 4,也就是说 4 没有左儿子,那么 10 必须为栈中某个节点的右儿子。那么如何找到这个节点呢?栈中的节点的顺序和它们在前序遍历中出现的顺序是一致的,而且每一个节点的右儿子都还没有被遍历过,那么这些节点的顺序和它们在中序遍历中出现的顺序一定是相反的。这是因为栈中的任意两个相邻的节点,前者都是后者的某个祖先。并且我们知道,栈中的任意一个节点的右儿子还没有被遍历过,说明后者一定是前者左儿子的子树中的节点,那么后者就先于前者出现在中序遍历中。
因此我们可以把 index 不断向右移动,并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点,那么说明我们在中序遍历中找到了栈顶节点,所以将 index 增加 1 并弹出栈顶节点,直到 index 对应的元素不等于栈顶节点。按照这样的过程,我们弹出的最后一个节点 x 就是 10 的双亲节点,这是因为 10 出现在了 x 与 x 在栈中的下一个节点的中序遍历之间,因此 10 就是 x 的右儿子。
回到我们的例子,我们会依次从栈顶弹出 4,5 和 8,并且将 index 向右移动了三次。我们将 10 作为最后弹出的节点 8 的右儿子,并将 10 入栈。
stack = [3, 9, 10]
index -> inorder[3] = 10
我们遍历 20。同理,index 恰好指向当前栈顶节点 10,那么我们会依次从栈顶弹出 10,9 和 3,并且将 index 向右移动了三次。我们将 20 作为最后弹出的节点 3 的右儿子,并将 20 入栈。stack = [20]
index -> inorder[6] = 15
我们遍历 15,将 15 作为栈顶节点 20 的左儿子,并将 15 入栈。stack = [20, 15]
index -> inorder[6] = 15
我们遍历 7。index 恰好指向当前栈顶节点 15,那么我们会依次从栈顶弹出 15 和 20,并且将 index 向右移动了两次。我们将 7 作为最后弹出的节点 20 的右儿子,并将 7 入栈。stack = [7]
index -> inorder[8] = 7
此时遍历结束,我们就构造出了正确的二叉树。算法
我们归纳出上述例子中的算法流程:
我们用一个栈和一个指针辅助进行二叉树的构造。初始时栈中存放了根节点(前序遍历的第一个节点),指针指向中序遍历的第一个节点;
我们依次枚举前序遍历中除了第一个节点以外的每个节点。如果 index 恰好指向栈顶节点,那么我们不断地弹出栈顶节点并向右移动 index,并将当前节点作为最后一个弹出的节点的右儿子;如果 index 和栈顶节点不同,我们将当前节点作为栈顶节点的左儿子;
无论是哪一种情况,我们最后都将当前的节点入栈。
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/construct-binary-tree-from-preorder-and-inorder-traversal/solution/cong-qian-xu-yu-zhong-xu-bian-li-xu-lie-gou-zao-9/
来源:力扣(LeetCode)
著作权归这作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
比较难想,多想几遍就好,多复习。?
?
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
if(inorder==null||inorder.length==0){
return null;
}
TreeNode root=new TreeNode(postorder[postorder.length-1]);
Deque<TreeNode> stack=new LinkedList<>();
stack.push(root);
int inorderIndex=inorder.length-1;
for(int i=postorder.length-2;i>=0;i--){
int postorderVal=postorder[i];
TreeNode node=stack.peek();
if(node.val!=inorder[inorderIndex]){
node.right=new TreeNode(postorderVal);
stack.push(node.right);
}else{
while(!stack.isEmpty()&& stack.peek().val==inorder[inorderIndex]){
node=stack.pop();
inorderIndex--;
}
node.left=new TreeNode(postorderVal);
stack.push(node.left);
}
}
return root;
}
}?其实这道题思路跟上一题大致相同,我们是从数组尾部开始计算的,即翻转数组,先遍历右字树,根,左子树。将后序数据放入栈,让中序遍历数据继续作为index值。
贴上leeco的题解吧
?
方法二:迭代
思路迭代法是一种非常巧妙的实现方法。迭代法的实现基于以下两点发现。
如果将中序遍历反序,则得到反向的中序遍历,即每次遍历右孩子,再遍历根节点,最后遍历左孩子。
如果将后序遍历反序,则得到反向的前序遍历,即每次遍历根节点,再遍历右孩子,最后遍历左孩子。
「反向」的意思是交换遍历左孩子和右孩子的顺序,即反向的遍历中,右孩子在左孩子之前被遍历。因此可以使用和「105. 从前序与中序遍历序列构造二叉树」的迭代方法类似的方法构造二叉树。对于后序遍历中的任意两个连续节点 u 和 v(在后序遍历中,u 在 v 的前面),根据后序遍历的流程,我们可以知道 u 和 v 只有两种可能的关系:u 是 v 的右儿子。这是因为在遍历到 u 之后,下一个遍历的节点就是 u 的双亲节点,即 v没有右儿子,并且 u 是 v 的某个祖先节点(或者 v 本身)的左儿子。如果 v?没有右儿子,那么上一个遍历的节点就是 v?的左儿子。如果 v 没有左儿子,则从 v 开始向上遍历 v?的祖先节点,直到遇到一个有左儿子(且 v 不在它的左儿子的子树中)的节点 v_a那么 u 就是 v_a?的左儿子。
第二种关系看上去有些复杂。我们举一个例子来说明其正确性,并在例子中给出我们的迭代算法。
例子
我们以树
? ? ? ? 3
? ? ? ?/ \
? ? ? 9 ?20
? ? ?/ \ ? \
? ? 15 10 ? 7
? ? ? ? ? ?/ \
? ? ? ? ? 5 ? 8
? ? ? ? ? ? ? ?\
? ? ? ? ? ? ? ? 4
为例,它的中序遍历和后序遍历分别为
inorder = [15, 9, 10, 3, 20, 5, 7, 8, 4]
postorder = [15, 10, 9, 5, 4, 8, 7, 20, 3]
我们用一个栈 stack 来维护「当前节点的所有还没有考虑过左儿子的祖先节点」,栈顶就是当前节点。也就是说,只有在栈中的节点才可能连接一个新的左儿子。同时,我们用一个指针 index 指向中序遍历的某个位置,初始值为 n - 1,其中 n 为数组的长度。index 对应的节点是「当前节点不断往右走达到的最终节点」,这也是符合反向中序遍历的,它的作用在下面的过程中会有所体现。首先我们将根节点 3 入栈,再初始化 index 所指向的节点为 4,随后对于后序遍历中的每个节点,我们依次判断它是栈顶节点的右儿子,还是栈中某个节点的左儿子。
我们遍历 20。20 一定是栈顶节点 3 的右儿子。我们使用反证法,假设 20 是 3 的左儿子,因为 20 和 3 中间不存在其他的节点,那么 3 没有右儿子,index 应该恰好指向 3,但实际上为 4,因此产生了矛盾。所以我们将 20 作为 3 的右儿子,并将 20 入栈。
stack = [3, 20]
index -> inorder[8] = 4
我们遍历 7,8 和 4。同理可得它们都是上一个节点(栈顶节点)的右儿子,所以它们会依次入栈。stack = [3, 20, 7, 8, 4]
index -> inorder[8] = 4
我们遍历 5,这时情况就不一样了。我们发现 index 恰好指向当前的栈顶节点 4,也就是说 4 没有右儿子,那么 5 必须为栈中某个节点的左儿子。那么如何找到这个节点呢?栈中的节点的顺序和它们在反向前序遍历中出现的顺序是一致的,而且每一个节点的左儿子都还没有被遍历过,那么这些节点的顺序和它们在反向中序遍历中出现的顺序一定是相反的。这是因为栈中的任意两个相邻的节点,前者都是后者的某个祖先。并且我们知道,栈中的任意一个节点的左儿子还没有被遍历过,说明后者一定是前者右儿子的子树中的节点,那么后者就先于前者出现在反向中序遍历中。
因此我们可以把 index 不断向左移动,并与栈顶节点进行比较。如果 index 对应的元素恰好等于栈顶节点,那么说明我们在反向中序遍历中找到了栈顶节点,所以将 index 减少 1 并弹出栈顶节点,直到 index 对应的元素不等于栈顶节点。按照这样的过程,我们弹出的最后一个节点 x 就是 5 的双亲节点,这是因为 5 出现在了 x 与 x 在栈中的下一个节点的反向中序遍历之间,因此 5 就是 x 的左儿子。
回到我们的例子,我们会依次从栈顶弹出 4,8 和 7,并且将 index 向左移动了三次。我们将 5 作为最后弹出的节点 7 的左儿子,并将 5 入栈。
stack = [3, 20, 5]
index -> inorder[5] = 5
我们遍历 9。同理,index 恰好指向当前栈顶节点 5,那么我们会依次从栈顶弹出 5,20 和 3,并且将 index 向左移动了三次。我们将 9 作为最后弹出的节点 3 的左儿子,并将 9 入栈。stack = [9]
index -> inorder[2] = 10
我们遍历 10,将 10 作为栈顶节点 9 的右儿子,并将 10 入栈。stack = [9, 10]
index -> inorder[2] = 10
我们遍历 15。index 恰好指向当前栈顶节点 10,那么我们会依次从栈顶弹出 10 和 9,并且将 index 向左移动了两次。我们将 15 作为最后弹出的节点 9 的左儿子,并将 15 入栈。stack = [15]
index -> inorder[0] = 15
此时遍历结束,我们就构造出了正确的二叉树。作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/construct-binary-tree-from-inorder-and-postorder-traversal/solution/cong-zhong-xu-yu-hou-xu-bian-li-xu-lie-gou-zao-14/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。