树形结构
树的概念
节点: 根节点、父节点、子节点、兄弟节点
空树: 一棵树可以没有任何节点
一棵树可以只有1个节点,也就是只有根节点
子树: 左子树、右子树
节点的度(degree): 子树的个数
树的度: 所有节点度中的最大值
叶子节点(leaf): 度为 0 的节点
非叶子节点: 度不为 0 的节点
层数(level): 根节点在第1层,根节点的子节点在第2层,以此类推(有些教程也从第0层开始计算)
节点的深度(depth): 从根节点到当前节点的唯一路径上的节点总数
节点的高度(height): 从当前节点到最远叶子节点的路径上的节点总数
树的深度: 所有节点深度中的最大值
树的高度: 所有节点高度中的最大值
树的深度等于树的高度
有序树 树中任意节点的子节点之间有顺序关系
无序树 树中任意节点的子节点之间没有顺序关系,也称为“自由树”
二叉树(Binary Tree)
二叉树的特点
- 每个节点的度最大为2(最多拥有2棵子树)
- 左子树和右子树是有顺序的(有序树)
- 即使某节点只有一棵子树,也要区分左右子树
真二叉树(Proper Binary Tree)
概念:所有节点的度都要么为 0,要么为 2

满二叉树(Full Binary Tree)
概念:最后一层节点的度都为0,其他节点的度都为2
性质:
-
假设满二叉树的高度为h(h≥1),那么有:
第i层的节点数量: 2 ^(i?1)
叶子节点数量:2 ^(h?1) -
同样高度的二叉树中,满二叉树的叶子节点数量最多、总节点数量最多
-
满二叉树一定是真二叉树,真二叉树不一定是满二叉树
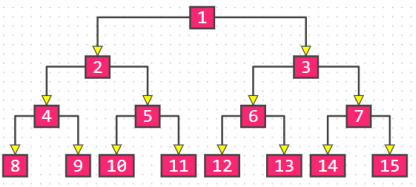
完全二叉树(Complete Binary Tree)
概念:叶子节点只会出现最后 2 层,且最后 1 层的叶子结点都靠左对齐
完全二叉树与满二叉树是很相似的,所以也可以这么定义,完全二叉树:对节点从上至下、左至右开始编号,其所有编号都能与相同高度的满二叉树中的编号对应

小结论:1、完全二叉树从根结点至倒数第2层是一棵满二叉树,2、满二叉树一定是完全二叉树,完全二叉树不一定是满二叉树
属性与节点
//数据元素
typedef struct data
{
int value;
data(int val)
{
value = val;
}
data()
{
value = 0;
}
}Item;
//树节点
typedef struct tree_node
{
Item item;
tree_node* pLeft;
tree_node* pRight;
}TreeNode;
//二叉树
typedef struct tree {
tree_node* pRoot;
int size;
}Tree;
二叉树的遍历
前序遍历
访问顺序:根节点、前序遍历左子树、前序遍历右子树 — (根节点访问在前)

遍历结果是:7、4、2、1、3、5、9、8、11、10、12
递归实现
//前序遍历 递归实现
void preorderTraversal(const TreeNode* pNode)
{
if (pNode == nullptr)
{
return;
}
//打印当前节点
std::cout << pNode->item.value << std::endl;
//遍历左子树
preorderTraversal(pNode->pLeft);
//遍历右子树
preorderTraversal(pNode->pRight);
}
非递归实现
- 利用栈先进后出的特性
- 设置node = root,将root入栈,循环执行以下操作,直到栈为空
- 弹出栈顶节点top,进行访问
- 将top.right入栈将top.left入栈
void preorderTraversal2(const Tree& tree)
{
stack<TreeNode*> s;
s.push(tree.pRoot);
while (!s.empty())
{
TreeNode* pNode = s.top();
s.pop();
//打印当前节点
cout << pNode->item.value << endl;
//先压入右节点,先压入的后弹出
if (pNode->pRight != nullptr)
{
s.push(pNode->pRight);
}
if (pNode->pLeft != nullptr)
{
s.push(pNode->pLeft);
}
}
}
中序遍历
访问顺序: — (根节点访问在中)
1、中序遍历左子树、根节点、中序遍历右子树 (如果是二叉搜索树,结果升序)
2、中序遍历右子树、根节点、中序遍历左子树 (如果是二叉搜索树,结果降序)

遍历结果是:1、2、3、4、5、7、8、9、10、11、12 (升序)
递归实现
void inorderTraversal(const TreeNode* pNode)
{
if (pNode == nullptr)
{
return;
}
//遍历左子树
inorderTraversal(pNode->pLeft);
//打印节点数据
std::cout << pNode->item.value << std::endl;
//遍历右子树
inorderTraversal(pNode->pRight);
}
非递归实现
实现步骤:
- 利用栈先进后出的特性
- 设置node = root,将root入栈,循环执行以下操作,直到栈为空
- 如果node!= null将node入栈,设置node = node.left
- 如果node == null如果栈为空,结束遍历,如果栈不为空,弹出栈顶元素并赋值给node,对node进行访问
- 设置node = node.right
void inorderTraversal2(const Tree& tree)
{
stack<TreeNode*> s;
TreeNode* pNode = tree.pRoot;
TreeNode* pTempNode;
do
{
while (pNode != nullptr)
{
s.push(pNode);
pNode = pNode->pLeft;
}
pTempNode = s.top();
s.pop();
cout << pTempNode->item.value << endl;
pNode = pTempNode->pRight;
} while (!s.empty() || pNode != nullptr);
}
后序遍历
访问顺序:后序遍历左子树、后序遍历右子树、根节点 — (根节点访问在后)

遍历结果是:1、3、2、5、4、8、10、12、11、9、7
递归实现
void postorderTraversal(const TreeNode* pNode)
{
if (pNode == nullptr)
{
return;
}
postorderTraversal(pNode->pLeft);
postorderTraversal(pNode->pRight);
std::cout << pNode->item.value << std::endl;
}
非递归实现
实现步骤:
- 利用栈先进后出的特性:
- 设置node = root,将root入栈,循环执行以下操作,直到栈为空
- 如果栈顶节点是叶子节点或者上一次访问的节点是栈顶节点的子节点,弹出栈顶节点,进行访问
- 否则,将栈顶节点的right、left按顺序入栈
void postorderTraversal2(const Tree& tree)
{
stack<TreeNode*> s;
TreeNode* pNode = tree.pRoot;
//记录上次访问的节点
TreeNode* pLastVisited = nullptr;
while (!s.empty() || pNode != nullptr)
{
while (pNode != nullptr)
{
s.push(pNode);
pNode = pNode->pLeft;
}
pNode = s.top();
s.pop();
//栈顶节点是叶子节点或者上一次访问的节点是栈顶节点的子节点
if (pNode->pRight == nullptr || pNode->pRight == pLastVisited)
{
cout << pNode->item.value << endl;
pLastVisited = pNode;
//这里node没有改变指向,所以需要指向null,否则会死循环
pNode = nullptr;
}
else
{
//既不是子节点且上一次访问的节点又不是栈顶节点的子节点话,代表是符节点,重新进栈
s.push(pNode);
pNode = pNode->pRight;
}
}
}
层序遍历
访问顺序:从上到下、从左到右依次访问每一个节点

遍历结果是:7、4、9、2、5、8、11、1、3、10、12
层序遍历采用迭代的方式实现,利用队列的先进先出性质,能很好的做到层序遍历
void levelOrderTraversal(const Tree& tree)
{
queue<TreeNode*> q;
q.push(tree.pRoot);
while (!q.empty())
{
TreeNode* pNode = q.front();
q.pop();
cout << pNode->item.value << endl;
if (pNode->pLeft != nullptr)
{
q.push(pNode->pLeft);
}
if (pNode->pRight != nullptr)
{
q.push(pNode->pRight);
}
}
}
完整代码
// ConsoleApplication32.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//
#include <iostream>
#include <stack>
#include <queue>
using namespace std;
//数据元素
typedef struct data
{
int value;
data(int val)
{
value = val;
}
data()
{
value = 0;
}
}Item;
//树节点
typedef struct tree_node
{
Item item;
tree_node* pLeft;
tree_node* pRight;
}TreeNode;
//二叉树
typedef struct tree {
tree_node* pRoot;
int size;
}Tree;
//初始化节点
void initTree(Tree& pTree);
//构造一个节点
TreeNode* makeNode(const Item& item);
//前序遍历 递归实现
void preorderTraversal(const TreeNode* pNode);
//中序遍历 递归实现
void inorderTraversal(const TreeNode* pNode);
//后序遍历 递归实现
void postorderTraversal(const TreeNode* pNode);
//前序遍历 非递归实现
void preorderTraversal2(const Tree& tree);
//中序遍历 非递归实现
void inorderTraversal2(const Tree& tree);
//后序遍历 非递归实现
void postorderTraversal2(const Tree& tree);
//层序遍历
void levelOrderTraversal(const Tree& tree);
int main()
{
Tree tree;
initTree(tree);
levelOrderTraversal(tree);
}
void initTree(Tree& pTree)
{
pTree.pRoot = makeNode(7);
pTree.pRoot->pLeft = makeNode(4);
pTree.pRoot->pRight = makeNode(9);
pTree.pRoot->pLeft->pLeft = makeNode(2);
pTree.pRoot->pLeft->pRight = makeNode(5);
pTree.pRoot->pLeft->pLeft->pLeft = makeNode(1);
pTree.pRoot->pLeft->pLeft->pRight = makeNode(3);
pTree.pRoot->pRight->pLeft = makeNode(8);
pTree.pRoot->pRight->pRight = makeNode(11);
pTree.pRoot->pRight->pRight->pLeft = makeNode(10);
pTree.pRoot->pRight->pRight->pRight = makeNode(12);
}
TreeNode* makeNode(const Item& item)
{
TreeNode* pNode = nullptr;
try {
pNode = new TreeNode;
}
catch (const std::bad_alloc& e)
{
cout << e.what() << endl;
cout << "Allocated memory exception." << endl;
}
pNode->item = item;
pNode->pLeft = nullptr;
pNode->pRight = nullptr;
return pNode;
}
//前序遍历 递归实现
void preorderTraversal(const TreeNode* pNode)
{
if (pNode == nullptr)
{
return;
}
//打印当前节点
std::cout << pNode->item.value << std::endl;
//遍历左子树
preorderTraversal(pNode->pLeft);
//遍历右子树
preorderTraversal(pNode->pRight);
}
void inorderTraversal(const TreeNode* pNode)
{
if (pNode == nullptr)
{
return;
}
//遍历左子树
inorderTraversal(pNode->pLeft);
//打印节点数据
std::cout << pNode->item.value << std::endl;
//遍历右子树
inorderTraversal(pNode->pRight);
}
void postorderTraversal(const TreeNode* pNode)
{
if (pNode == nullptr)
{
return;
}
postorderTraversal(pNode->pLeft);
postorderTraversal(pNode->pRight);
std::cout << pNode->item.value << std::endl;
}
void preorderTraversal2(const Tree& tree)
{
stack<TreeNode*> s;
s.push(tree.pRoot);
while (!s.empty())
{
TreeNode* pNode = s.top();
s.pop();
//打印当前节点
cout << pNode->item.value << endl;
//先压入右节点,先压入的后弹出
if (pNode->pRight != nullptr)
{
s.push(pNode->pRight);
}
if (pNode->pLeft != nullptr)
{
s.push(pNode->pLeft);
}
}
}
void inorderTraversal2(const Tree& tree)
{
stack<TreeNode*> s;
TreeNode* pNode = tree.pRoot;
TreeNode* pTempNode;
do
{
while (pNode != nullptr)
{
s.push(pNode);
pNode = pNode->pLeft;
}
pTempNode = s.top();
s.pop();
cout << pTempNode->item.value << endl;
pNode = pTempNode->pRight;
} while (!s.empty() || pNode != nullptr);
}
void postorderTraversal2(const Tree& tree)
{
stack<TreeNode*> s;
TreeNode* pNode = tree.pRoot;
//记录上次访问的节点
TreeNode* pLastVisited = nullptr;
while (!s.empty() || pNode != nullptr)
{
while (pNode != nullptr)
{
s.push(pNode);
pNode = pNode->pLeft;
}
pNode = s.top();
s.pop();
//栈顶节点是叶子节点或者上一次访问的节点是栈顶节点的子节点
if (pNode->pRight == nullptr || pNode->pRight == pLastVisited)
{
cout << pNode->item.value << endl;
pLastVisited = pNode;
//这里node没有改变指向,所以需要指向null,否则会死循环
pNode = nullptr;
}
else
{
//既不是子节点且上一次访问的节点又不是栈顶节点的子节点话,代表是符节点,重新进栈
s.push(pNode);
pNode = pNode->pRight;
}
}
}
void levelOrderTraversal(const Tree& tree)
{
queue<TreeNode*> q;
q.push(tree.pRoot);
while (!q.empty())
{
TreeNode* pNode = q.front();
q.pop();
cout << pNode->item.value << endl;
if (pNode->pLeft != nullptr)
{
q.push(pNode->pLeft);
}
if (pNode->pRight != nullptr)
{
q.push(pNode->pRight);
}
}
}