如何构造一个大顶堆(C实现)
基础知识
堆是一种二叉树结构,但是他的物理保存是一个数组,如下图

实际的保存形式为
{5,4,1,25,68,8,1,5,2,3}
设每个结点下标为i
则左孩子:2i+1
右孩子:2i+2
最后一个非叶子结点:arr.length/2-1 //因为 每一个结点的孩子结点下标不能超过数组长度arr.length,所以非叶子结点孩子下标2*i+1<=arr.length-1 ,下标从0开始
**大根堆的概念:**从根结点开始,每一个结点的值都大于其两个孩子结点的值
接下来我们通过算法将该数组构造成一个大根堆
构造大根堆
算法思路: 如果以某结点 i 为树,它的左右子树都是一个大根堆,那我们只要将arr[i] 与 max(arr[2*i+1], arr[2*i+2])进行比较,如果arr[i] < max(arr[2*i+1], arr[i*2+2]),就将两者交换,然后继续往下交换,直到arr[i] > max(arr[i*2+1], arr[i*2+2]),或者i*2+1>length,就可以完成大根堆的构造
现在问题就是,如果保证左右子树都是大根堆,我们通过动态规划的思想,从最后一个非叶子结点一直往上推,就能保证每一个结点的左右子树都为大根堆
c语言实现如下:
#include<stdio.h>
#include<stdlib.h>
void createHeap(int arr[10]);
void upAdjust(int root, int arr[10]);
int main(){
int arr[10] = {5,4,1,25,68,8,1,5,2,3};
createHeap(arr);
return 0;
}
void createHeap(int arr[10] ){
int parent = 10/2 - 1; //最后一个非叶子结点 2*x+1 <= arr.length-1
for(int i=parent; i>=0; i--){
upAdjust(i, arr);
}
for(int i=0; i<10; i++)
printf("%2d ", arr[i]);
printf("\n");
for(int i=0; i<10; i++)
printf("%2d ", i);
}
void upAdjust(int root, int arr[10]){
int parent = root;
int child = 2*root+1;
if(child+1<10 && arr[child]<arr[child+1])
child=child+1;
while(child < 10){
if(arr[parent]<arr[child]){
int tmp = arr[parent];
arr[parent] = arr[child];
arr[child] = tmp;
parent=child;
child=parent*2+1;
}else{
break;
}
}
}
运行结果如下:
图如下:
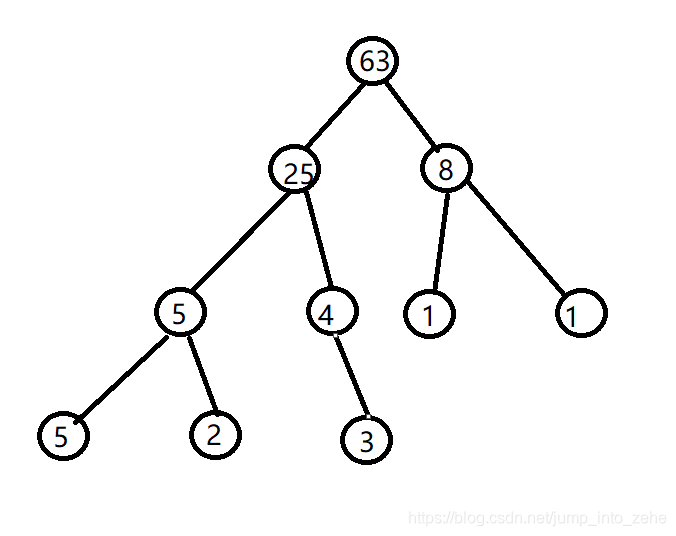
构造大根堆的意义有很多,可以解答topN问题,比如在一个无序的数组中,我们想要拿到最小或者最大的几个元素,就可以使用大根堆或者小根堆,也可以用来当做优先队列,堆排序实际上就是冒泡排序的升级版,选出堆顶的过程其实也类似与冒泡