?图的定义:
由顶点集V(Vertex)和边集E(Edge)组成,记为G=(V,E),其中V(G)表示图G中顶点的有限非空集;树是一对多,而图是多对多,一个顶点可以连接多个顶点。由于顶点在位置上不一样,看起来不一样,看起来不一样,其实是一样的。
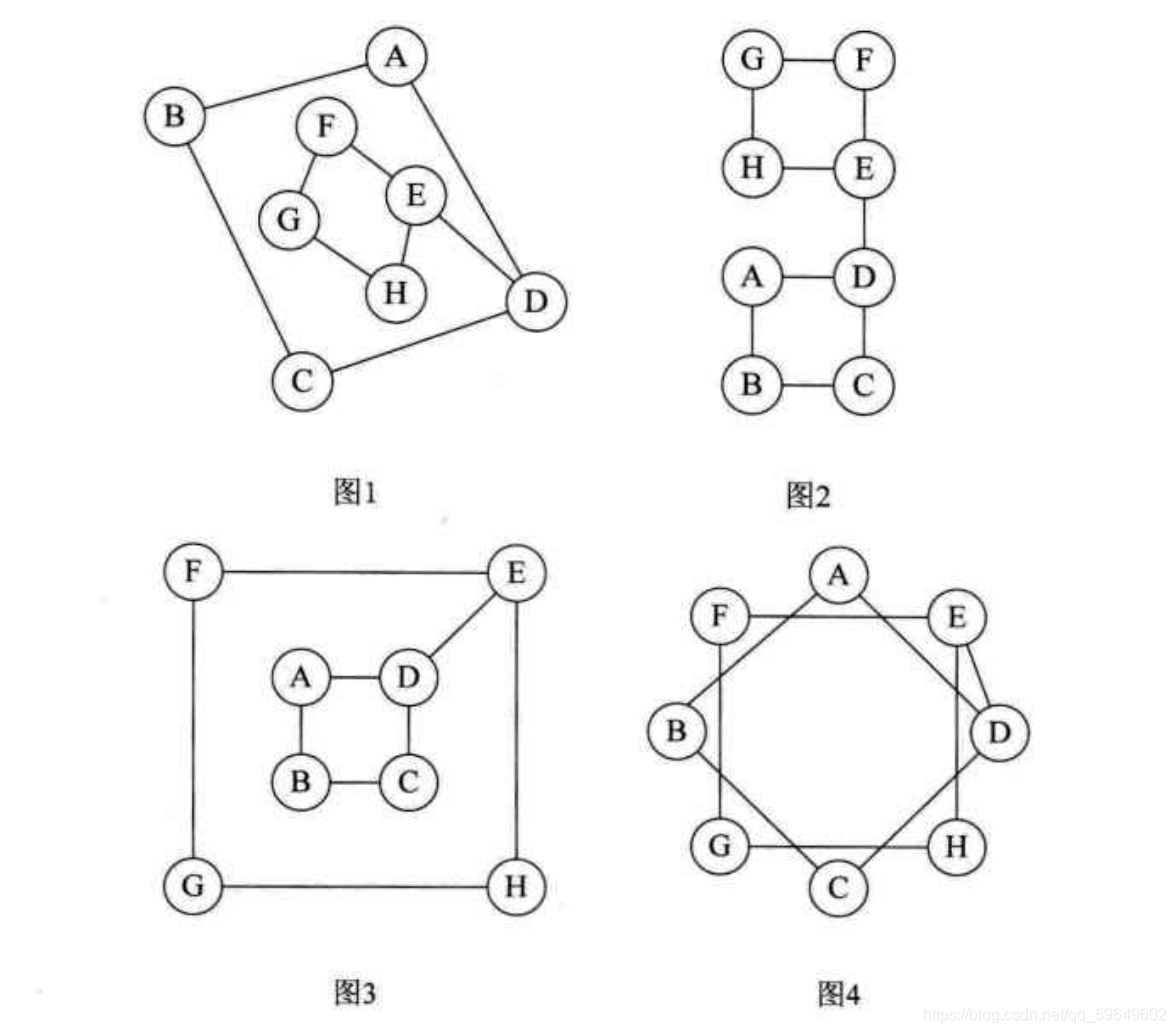
?
- 图按照有无方向分为无向图和有向图。无向图由顶点和边构成,有向图由顶点和弧构成,弧有弧尾和弧头之分。
- ?图按照边或弧的多少分稀疏图和稠密图。如果任意两个顶点之间都存在边叫完全图,有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
- 图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度,有向图顶点分为入度和出度。图上的边或弧上带权则称为网。
- ?无向图中连通且n个顶点n-1条边叫生成树。有向图中顶点入度为0其余顶点入度为1的叫有向树。-一个有向图由若干棵有向树构成生成森林。
?
?
?
图的存储结构
1. 邻接表
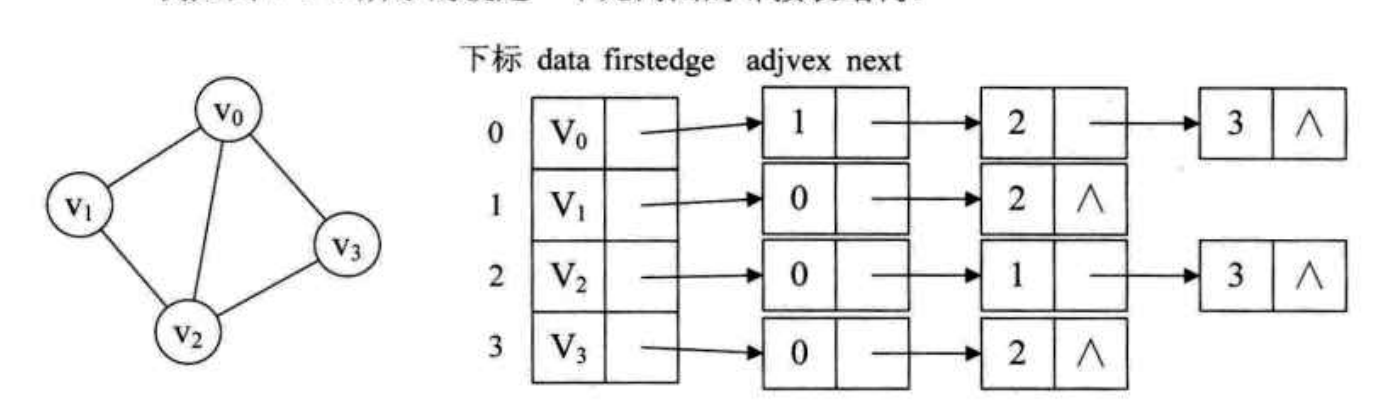
?
用链来存储与该结点相连的结点;
邻接表创建的结构体定义:
typedef int Status;?? ?/* Status是函数的类型,其值是函数结果状态代码,如OK等 */
typedef char VertexType; /* 顶点类型应由用户定义 */
typedef int EdgeType; /* 边上的权值类型应由用户定义 */
typedef struct EdgeNode /* 边表结点 ?*/
{
?? ?int adjvex; ? ?/* 邻接点域,存储该顶点对应的下标 */
?? ?EdgeType info;?? ??? ?/* 用于存储权值,对于非网图可以不需要 */
?? ?struct EdgeNode *next; /* 链域,指向下一个邻接点 */
}EdgeNode;
typedef struct VertexNode /* 顶点表结点 */
{
?? ?VertexType data; /* 顶点域,存储顶点信息 */
?? ?EdgeNode *firstedge;/* 边表头指针 */
}VertexNode, AdjList[MAXVEX];
typedef struct
{
?? ?AdjList adjList;?
?? ?int numNodes,numEdges; /* 图中当前顶点数和边数 */
}GraphAdjList;
邻接表的创建
void ?CreateALGraph(GraphAdjList *G)
{
?? ?int i,j,k;
?? ?EdgeNode *e;
?? ?printf("输入顶点数和边数:\n");
?? ?scanf("%d,%d",&G->numNodes,&G->numEdges); /* 输入顶点数和边数 */
?? ?for(i = 0;i < G->numNodes;i++) /* 读入顶点信息,建立顶点表 */
?? ?{
?? ??? ?scanf(&G->adjList[i].data); ?? ?/* 输入顶点信息 */
?? ??? ?G->adjList[i].firstedge=NULL; ?? ?/* 将边表置为空表 */
?? ?}
?? ?
?? ?
?? ?for(k = 0;k < G->numEdges;k++)/* 建立边表 */
?? ?{
?? ??? ?printf("输入边(vi,vj)上的顶点序号:\n");
?? ??? ?scanf("%d,%d",&i,&j); /* 输入边(vi,vj)上的顶点序号 */
?? ??? ?e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */
?? ??? ?e->adjvex=j;?? ??? ??? ??? ??? ?/* 邻接序号为j */ ? ? ? ? ? ? ? ? ? ? ? ??
?? ??? ?e->next=G->adjList[i].firstedge;?? ?/* 将e的指针指向当前顶点上指向的结点 */
?? ??? ?G->adjList[i].firstedge=e;?? ??? ?/* 将当前顶点的指针指向e */ ? ? ? ? ? ? ??
?? ??? ?
?? ??? ?e=(EdgeNode *)malloc(sizeof(EdgeNode)); /* 向内存申请空间,生成边表结点 */
?? ??? ?e->adjvex=i;?? ??? ??? ??? ??? ?/* 邻接序号为i */ ? ? ? ? ? ? ? ? ? ? ? ??
?? ??? ?e->next=G->adjList[j].firstedge;?? ?/* 将e的指针指向当前顶点上指向的结点 */
?? ??? ?G->adjList[j].firstedge=e;?? ??? ?/* 将当前顶点的指针指向e */ ? ? ? ? ? ? ??
? ? ? }
?? ?}
?? ?
2.还有十字链表,邻接多重表等
深度优先搜索遍历
? ? 假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止,如果旁边的点都被访问了,则退回上一个顶点再进行访问搜索。显然,深度优先搜索是一个递归的过程
? ?代码实现如下:
void DFS(MGraph G, int i)
{
?? ?int j;
??? ?visited[i] = TRUE;
??? ?printf("%c ", G.vexs[i]);/* 打印顶点,也可以其它操作 */
?? ?for(j = 0; j < G.numVertexes; j++)
?? ??? ?if(G.arc[i][j] == 1 && !visited[j])
??? ??? ??? ?DFS(G, j);/* 对为访问的邻接顶点递归调用 */
}
/* 邻接矩阵的深度遍历操作 */
void DFSTraverse(MGraph G)
{
?? ?int i;
??? ?for(i = 0; i < G.numVertexes; i++)
??? ??? ?visited[i] = FALSE; /* 初始所有顶点状态都是未访问过状态 */
?? ?for(i = 0; i < G.numVertexes; i++)
??? ??? ?if(!visited[i]) /* 对未访问过的顶点调用DFS,若是连通图,只会执行一次 */?
?? ??? ??? ?DFS(G, i);
}
广度优先搜索
? 广度优先遍历类似于二叉树的层序遍历,可以利用队列来实现。对于利用邻接表存储的图,我们给定任意一顶点,将与改顶点连接的链表遍历即可,一层一层的遍历。但是要注意可能会出现重复遍历,所以我们要添加标记。
? 下面代码是对于邻接矩阵的广度优先遍历
- ? 结构体定义(用栈来存放遍历过的点):
```c
typedef struct
{
?? ?VertexType vexs[MAXVEX]; /* 顶点表 */
?? ?EdgeType arc[MAXVEX][MAXVEX];/* 邻接矩阵,可看作边表 */
?? ?int numVertexes, numEdges; /* 图中当前的顶点数和边数 */?
}MGraph;
/* 用到的队列结构与函数********************************** */
/* 循环队列的顺序存储结构 */
typedef struct
{
?? ?int data[MAXSIZE];
?? ?int front; ? ??? ?/* 头指针 */
?? ?int rear;?? ??? ?/* 尾指针,若队列不空,指向队列尾元素的下一个位置 */
}Queue;
/* 初始化一个空队列Q */
Status InitQueue(Queue *Q)
{
?? ?Q->front=0;
?? ?Q->rear=0;
?? ?return ?OK;
}
```- 对矩阵遍历:
void BFSTraverse(MGraph G)
{
?? ?int i, j;
?? ?Queue Q;
?? ?for(i = 0; i < G.numVertexes; i++)
? ? ? ??? ?visited[i] = FALSE;
? ? InitQueue(&Q);?? ??? ?/* 初始化一辅助用的队列 */
? ? for(i = 0; i < G.numVertexes; i++) ?/* 对每一个顶点做循环 */
? ? {
?? ??? ?if (!visited[i])?? ?/* 若是未访问过就处理 */
?? ??? ?{
?? ??? ??? ?visited[i]=TRUE;?? ??? ?/* 设置当前顶点访问过 */
?? ??? ??? ?printf("%c ", G.vexs[i]);/* 打印顶点,也可以其它操作 */
?? ??? ??? ?EnQueue(&Q,i);?? ??? ?/* 将此顶点入队列 */
?? ??? ??? ?while(!QueueEmpty(Q))?? ?/* 若当前队列不为空 */
?? ??? ??? ?{
?? ??? ??? ??? ?DeQueue(&Q,&i);?? ?/* 将队对元素出队列,赋值给i */
?? ??? ??? ??? ?for(j=0;j<G.numVertexes;j++)?
?? ??? ??? ??? ?{?
?? ??? ??? ??? ??? ?/* 判断其它顶点若与当前顶点存在边且未访问过 ?*/
?? ??? ??? ??? ??? ?if(G.arc[i][j] == 1 && !visited[j])?
?? ??? ??? ??? ??? ?{?
??? ??? ??? ??? ??? ??? ?visited[j]=TRUE;?? ??? ??? ?/* 将找到的此顶点标记为已访问 */
?? ??? ??? ??? ??? ??? ?printf("%c ", G.vexs[j]);?? ?/* 打印顶点 */
?? ??? ??? ??? ??? ??? ?EnQueue(&Q,j);?? ??? ??? ??? ?/* 将找到的此顶点入队列 ?*/
?? ??? ??? ??? ??? ?}?
?? ??? ??? ??? ?}?
?? ??? ??? ?}
?? ??? ?}
?? ?}
}本内容转载至:http://blog.bools.cn/archives/1019

?