1.概念
- 平衡二叉树的每个结点左右高度之差不超过1(定义)
- 平衡二叉树是在二叉排序树的基础上实现的,如果是普通的树也能够实现平衡,但并没有什么作用。而在二叉排序树上实现平衡则能够减少检索量,提高二叉排序树的性能
- 平衡二叉树是于二叉排序树的创建同步的,二叉排序树每创建一个结点则对二叉树进行平衡
2.实现步骤
在建立二叉排序树的过程中:
-
创建需要插入二叉排序树的结点
-
对二叉树进行二分查找,找到适合插入的位置插入;同时记录当前插入的点,记作Current_Node
-
对当前的二叉排序树,递归建立子树高度 Cal_Tree_High()
-
对当前的二叉树进行层次遍历,根据上一步的子树高度得到各个结点的平衡因子 Balance
-
查找当前二叉排序树的最小不平衡子树(建立三叉链表,根据当前结点Current_Node自底向上查找父节点)
-
找到最小不平衡子树的根节点时分四种情况讨论(每次操作针对的都是根节点) 👇👇👇
-
速记:左左 和右右都是反向下旋 左右和右左同向下旋
-
要注意的一个点是每种情况的根节点和对应的左/右孩子的Balance是确定的;四种情况实际上就是两种动作点坐下旋和点右下旋,注意选择好点就行
1.插入的结点在根节点的左孩子的左子树(左左)
A:2 B:1 -> A:0 B:0 ******A右下旋
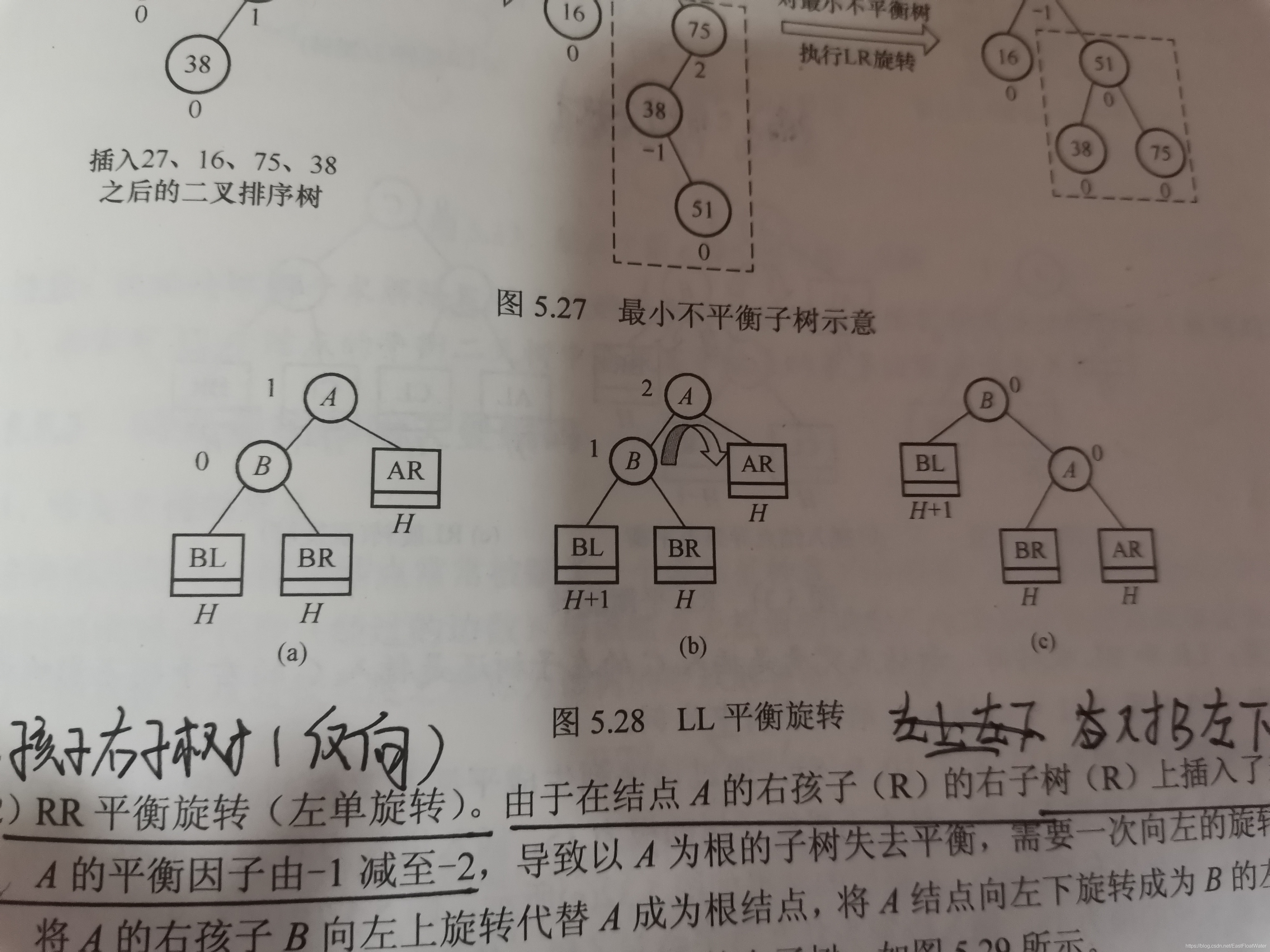
2.插入的结点在根节点右孩子的右子树
A:-2 B:-1 -> A:0 B:0 ******A左下旋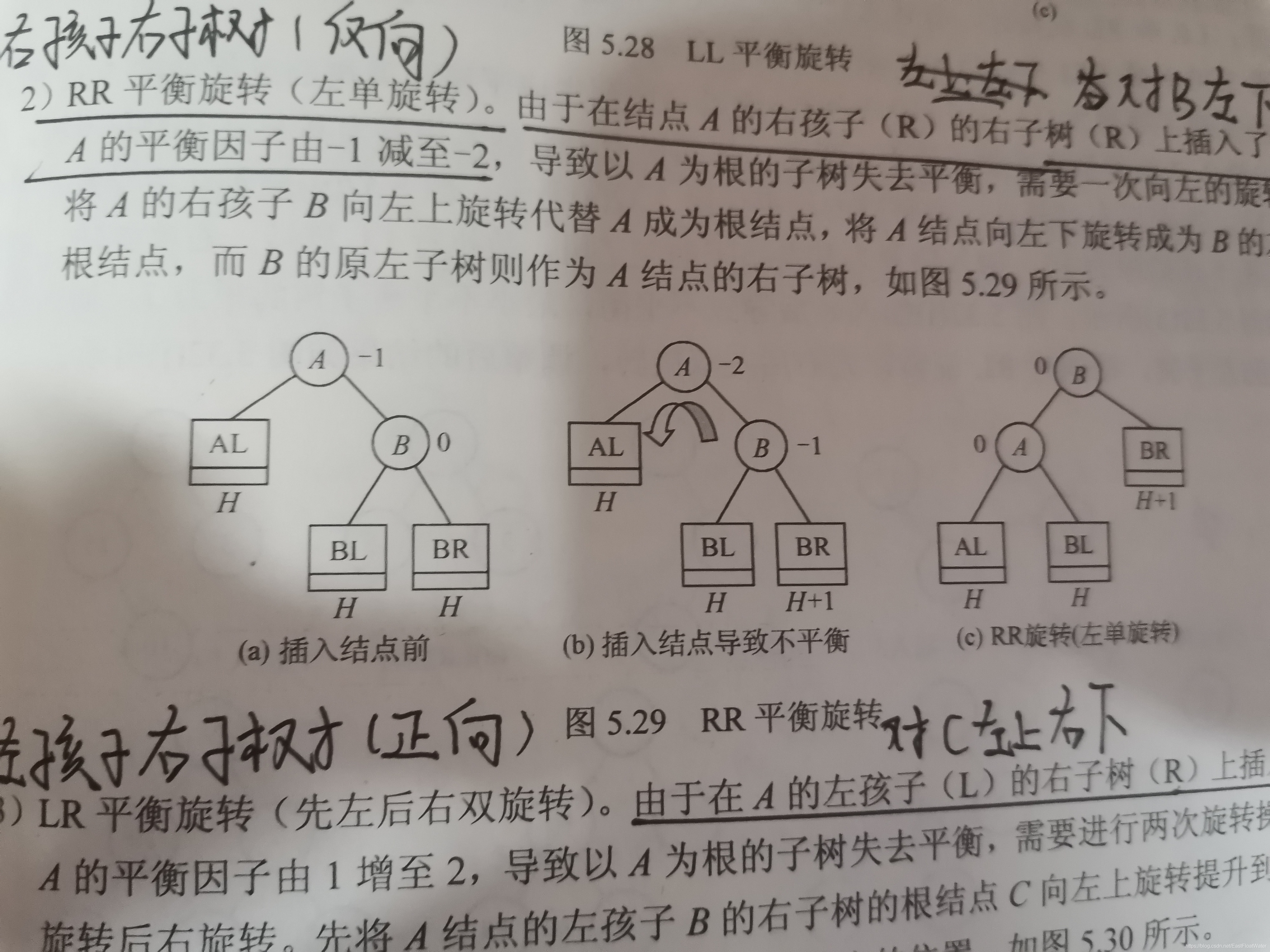
3.插入的结点在根节点左孩子的右子树
**A:2 B:-1 C:1-> A:2 B:0 C:2 ->A:-1 B:0 C:0 ** ******B左下旋转 A右下旋
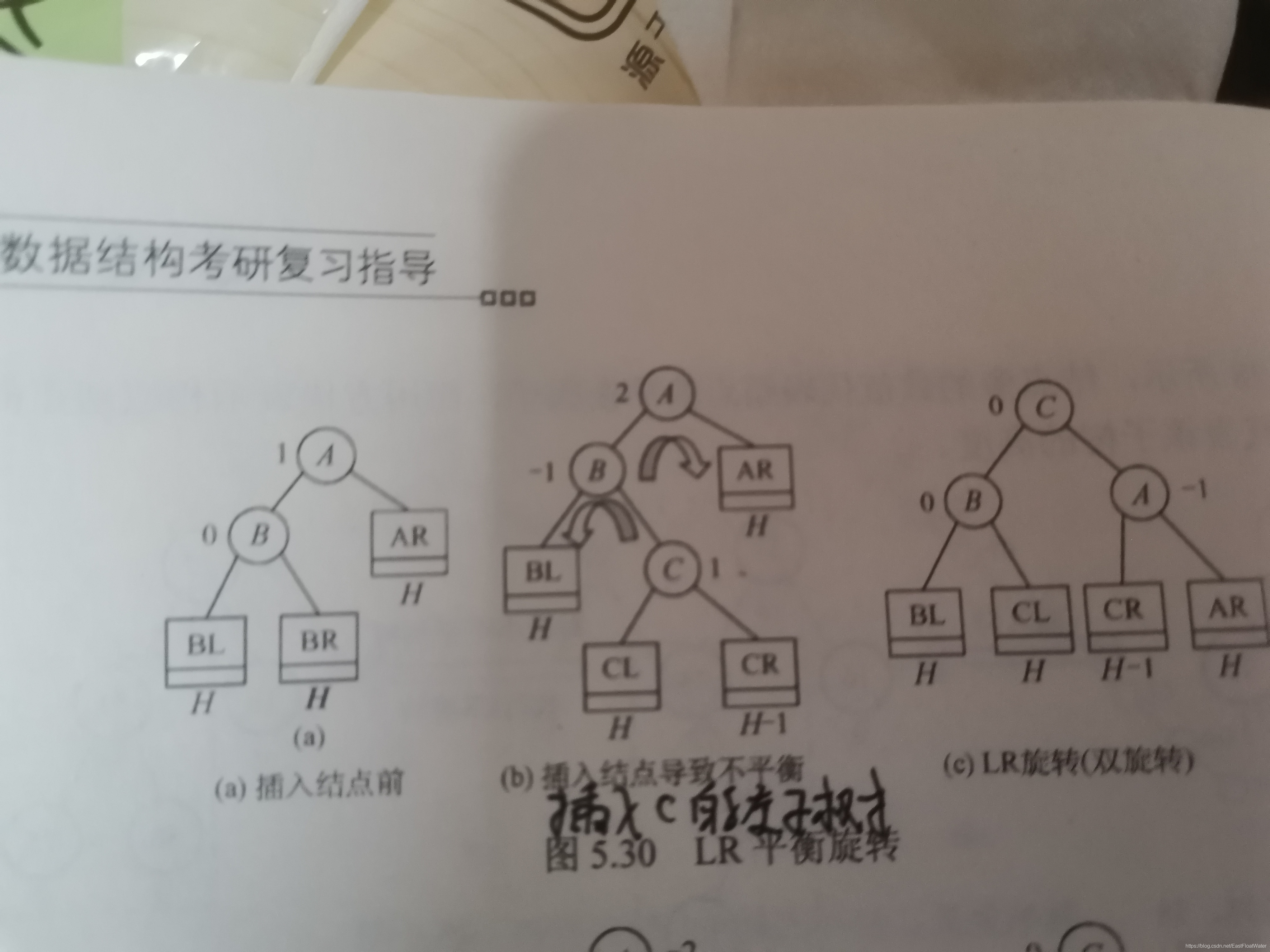
4.插入的结点在根节点的右孩子的左子树
**A:-2 B:1 C:1-> A:-2 B:-1 C:-1 ->A:0 B:-1 C:0 ** ******B右下旋转 A左下旋
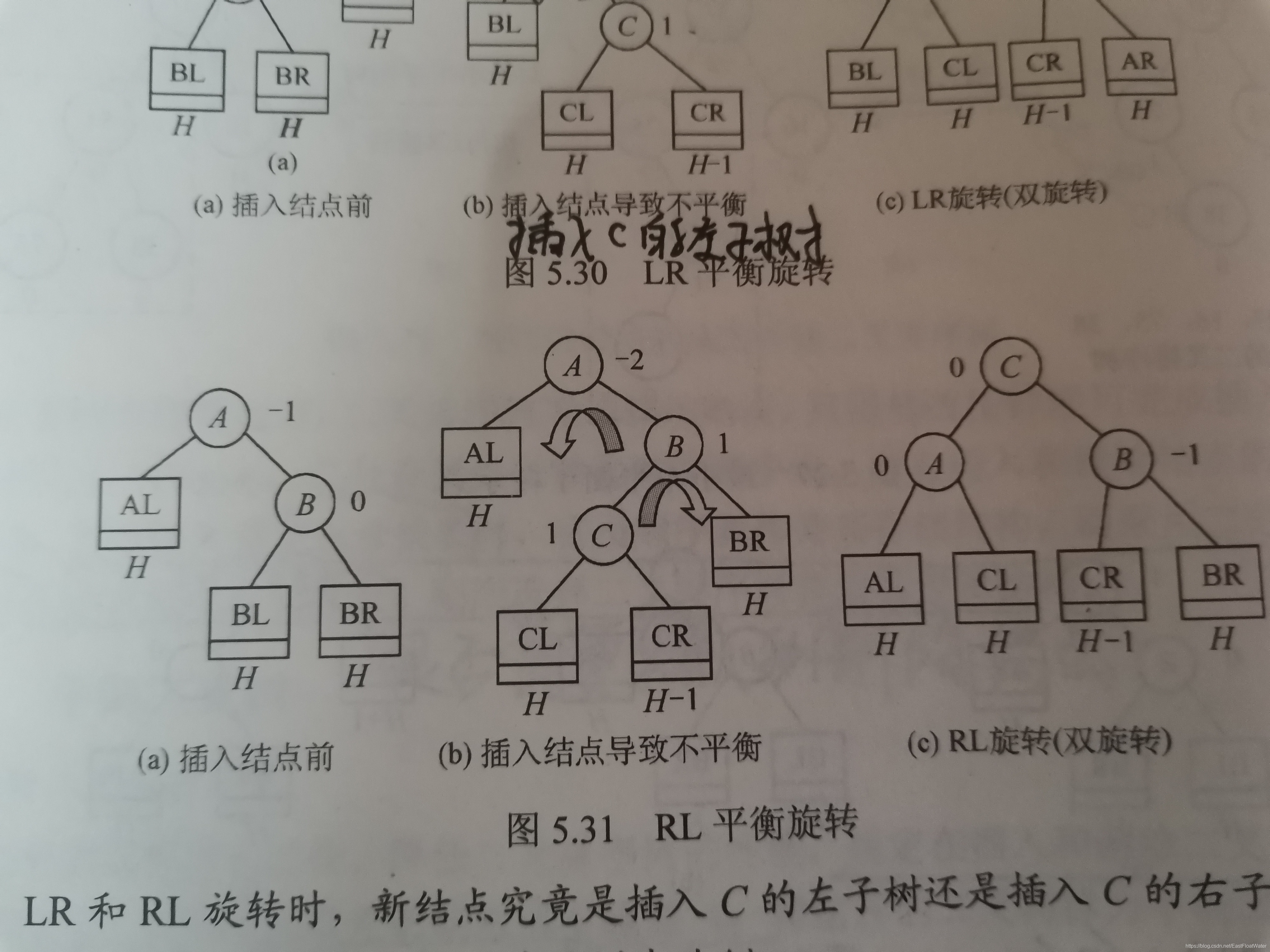
3.代码
#pragma once
#include"LinkedStack.h"
#include"Queue.h"
class BstNode {
public:
int data;
int balance;//平衡因子
int high;//当前结点(子树)的高度
BstNode* lchild;
BstNode* rchild;
BstNode* parent;
BstNode(int data) {
this->data = data;
this->balance = 0;
this->high = 0;
lchild = nullptr;
rchild = nullptr;
parent = nullptr;
}
};
class BST {
private:
BstNode *root;
BstNode* Current_Node=nullptr;
public:
BST(int* a, int length) {
root = nullptr;
BST_Create(a, length);
int b = 0;
};
BstNode* GetRoot() {
return this->root;
}
//搜索二叉排序树中的某个结点
BstNode* BST_Search(BstNode* Node,int data) {
if (Node == nullptr)return nullptr;
if (data == Node->data)return Node;
if (data < Node->data)
{
return BST_Search(Node->lchild, data);
}
if (data > Node->data) {
return BST_Search(Node->rchild, data);
}
};
//在二叉排序树中插入值
void BST_Insert(BstNode* &Node,BstNode* &parent, int data) {
if (Node == nullptr) {
Node = new BstNode(data);
Node->parent = parent;
Current_Node = Node;
return;
}
Node->parent = parent;
if (data == Node->data) { return; }
if (data < Node->data) {
BST_Insert(Node->lchild, Node,data);
}
if (data > Node->data) {
BST_Insert(Node->rchild,Node, data);
}
};
//递归计算各子树的高度
int Cal_Tree_High(BstNode* Node) {
if (Node == nullptr)return 0;
if (Node->lchild == nullptr && Node->rchild == nullptr) {
Node->high =1 ;
}
else if (Node->lchild != nullptr && Node->rchild == nullptr) {
Node->high = Cal_Tree_High(Node->lchild)+1;
}
else if (Node->lchild == nullptr && Node->rchild == nullptr) {
Node->high = Cal_Tree_High(Node->rchild)+1;
}
else {
Node->high = (Cal_Tree_High(Node->lchild)> Cal_Tree_High(Node->rchild)? Cal_Tree_High(Node->lchild): Cal_Tree_High(Node->rchild)) + 1;
}
return Node->high;
}
//层次遍历计算各结点的平衡因子
void Cal_Balance(BstNode* Node) {
Queue<BstNode*>* que = new Queue<BstNode*>();
BstNode* Que_Head=nullptr;
que->EnQueue(Node);
while (!que->Empty()) {
que->DeQueue(Que_Head);
Que_Head->balance = (Que_Head->lchild == nullptr ? 0 : Que_Head->lchild->high) - (Que_Head->rchild == nullptr ? 0 : Que_Head->rchild->high);
que->EnQueue(Que_Head->lchild);
que->EnQueue(Que_Head->rchild);
}
}
//平衡二叉树
void BST_Balance(BstNode* Current_Node) {
while (Current_Node->parent!=nullptr && abs(Current_Node->balance) < 2) {
Current_Node = Current_Node->parent;
}
//左孩子的左右子树插入结点
if(Current_Node->balance>1){
//左孩子的左子树插入结点 LL
if(Current_Node->lchild->balance==1){
RD_Rotate(Current_Node);
return;
}
//左孩子的右子树插入结点 LR
if(Current_Node->lchild->balance==-1){
LD_Rotate(Current_Node->lchild);
RD_Rotate(Current_Node);
return;
}
}
//右孩子的左右子树插入结点
else if(Current_Node->balance<-1){
//右孩子的右子树插入结点
if (Current_Node->rchild->balance == -1) {
LD_Rotate(Current_Node);
return;
}
//右孩子的左子树插入结点
if (Current_Node->rchild->balance == 1) {
RD_Rotate(Current_Node->rchild);
LD_Rotate(Current_Node);
return;
}
}
}
//左下旋,必是右孩子
void LD_Rotate(BstNode* Node){
BstNode* child = Node->rchild;
Node->rchild = child->lchild;
child->lchild = Node;
child->balance = 0;
Node->balance = 0;
if (Node->parent == nullptr) { root = child; return; }
if (Node->parent->lchild == Node) { Node->parent->lchild = child; }
if (Node->parent->rchild == Node) { Node->parent->rchild = child; }
}
//右下旋,必是左孩子
void RD_Rotate(BstNode* Node){
BstNode* child = Node->lchild;
Node->lchild = child->rchild;
child->rchild = Node;
child->balance = 0;
Node->balance = 0;
if (Node->parent == nullptr) { root = child; return; }
if (Node->parent->lchild == Node) { Node->parent->lchild = child; }
if (Node->parent->rchild == Node) { Node->parent->rchild = child; }
}
//使用数组创建二叉排序树
void BST_Create(int*a,int length) {
if (a == nullptr)return;
BstNode* parent = nullptr;
for (int i = 0; i < length; i++) {
BST_Insert(root,parent,a[i]);
Cal_Tree_High(root);
Cal_Balance(root);
BST_Balance(this->Current_Node);
}
};
//删除二叉排序树中的某个结点
void BST_Delete(BstNode* Node,int data) {
BstNode* current_node = BST_Search(Node, data);
//被删除结点左右子树为空
if (current_node->lchild == nullptr && current_node->rchild == nullptr) {
//处理当前结点的父节点,让其指向nullprt
if (current_node == current_node->parent->lchild)current_node->parent->lchild = nullptr;
else if (current_node == current_node->parent->rchild)current_node->parent->rchild = nullptr;
delete current_node;
return;
}
//被删除结点左子树为空
if (current_node->lchild==nullptr && current_node->rchild!=nullptr){
if (current_node == current_node->parent->lchild) {
current_node->parent->lchild = current_node->rchild;
delete current_node;
}
else if (current_node == current_node->parent->rchild) {
current_node->parent->rchild = current_node->rchild;
delete current_node;
}
return;
}
//被删除结点右子树为空
if (current_node->lchild != nullptr && current_node->rchild == nullptr) {
if (current_node == current_node->parent->lchild) {
current_node->parent->lchild = current_node->lchild;
delete current_node;
}
else if (current_node == current_node->parent->rchild) {
current_node->parent->rchild = current_node->lchild;
delete current_node;
}
return;
}
//被删除结点左右子树都不为空
if (current_node->lchild != nullptr && current_node->rchild != nullptr) {
BstNode* After_Node = current_node->rchild;
//找到被删除结点按顺序排列的下一个结点
while (After_Node->lchild != nullptr) {
After_Node = After_Node->lchild;
}
//记录下一结点的值
int data = After_Node->data;
//递归删除下一结点,继续用分三种情况分析
BST_Delete(current_node, After_Node->data);
current_node->data = data;
return;
}
int a;
};
void BST_Foreach(BstNode* Node){
if (Node == nullptr)return;
BST_Foreach(Node->lchild);
Visit(Node);
BST_Foreach(Node->rchild);
}
void Visit(BstNode* Node) {
std::cout << Node->data<<std::endl;
}
};
-------main
#include <iostream>
#include"BST.h"
using namespace std;
int main()
{
int a[] = {34,23,15,98,115,28,107};
BST* tree = new BST(a,7);
BstNode* root = tree->GetRoot();
int b = 0;
}