[数据结构与算法]【LeetCode | 二叉树前、中、后序遍历{迭代法}实现】

1.前序遍历

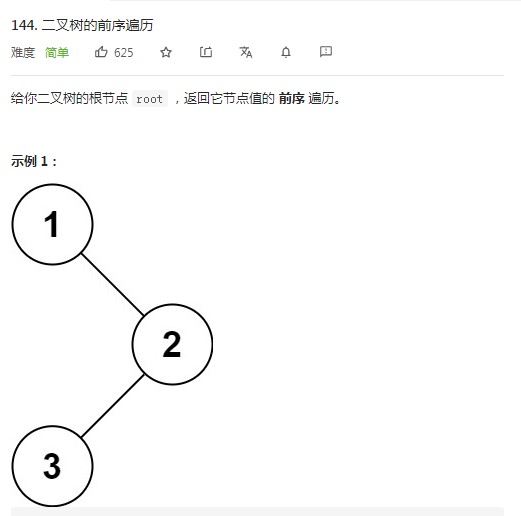
// 解题思路:利用栈的原理实现以迭代方法来前序遍历(根左右)二叉树
class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if(root == nullptr) return result;

        st.push(root);
        while(!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);

            if(node->right) st.push(node->right);  // 因为栈是后进先出，因此访问顺序与前序遍历顺序相反
            if(node->left) st.push(node->left);
        }
        return result;
    }
};

2.中序遍历

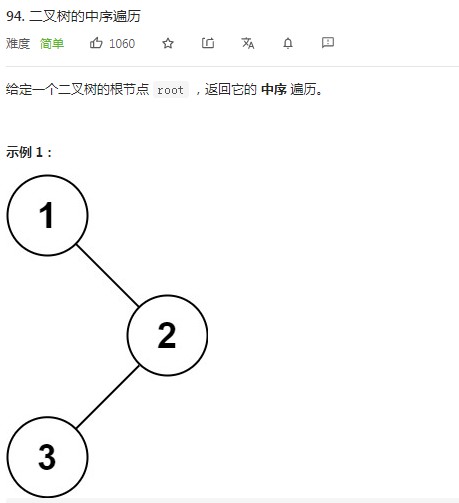
// 解题思路:利用栈的原理实现以迭代方法来中序遍历(左根右)二叉树,由于每个节点的访问顺序与处理顺序不一致，因此需要额外的指针cur来帮助访问节点,栈用来处理节点上的元素
class Solution{
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;

        TreeNode* cur = root;
        while (cur != nullptr || !st.empty())  // 指针cur来访问节点，访问到叶子节点则终止 
        {
            if(cur != nullptr) {
                st.push(cur);     // 将已经访问过的节点存入栈中
                cur = cur->left;  // 左
            } else {
                cur = st.top();
                st.pop();
                result.push_back(cur->val); // 根
                cur = cur->right;   // 右
            }
        }
        return result;
    }
};

3.后序遍历

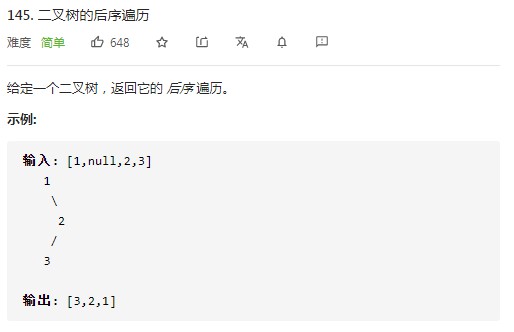
// 解题思路:利用栈的原理实现以迭代方法来后序遍历(左右根)二叉树
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> result;
        stack<TreeNode*> st;
        if(root == nullptr) return result;

        st.push(root);
        while(!st.empty()) {
            TreeNode* node = st.top();
            st.pop();
            result.push_back(node->val);

            if(node->left) st.push(node->left);  // 因为栈是后进先出，因此访问顺序与前序遍历顺序相反
            if(node->right) st.push(node->right);
        }
        reverse(result.begin(), result.end());  // 此时，result中的存在顺序是根右左，因此需要对result数组翻转一下即左右根
        return result;
    }
};