?
文章目录
?
?
??
二叉树的存储结构
顺序存储结构
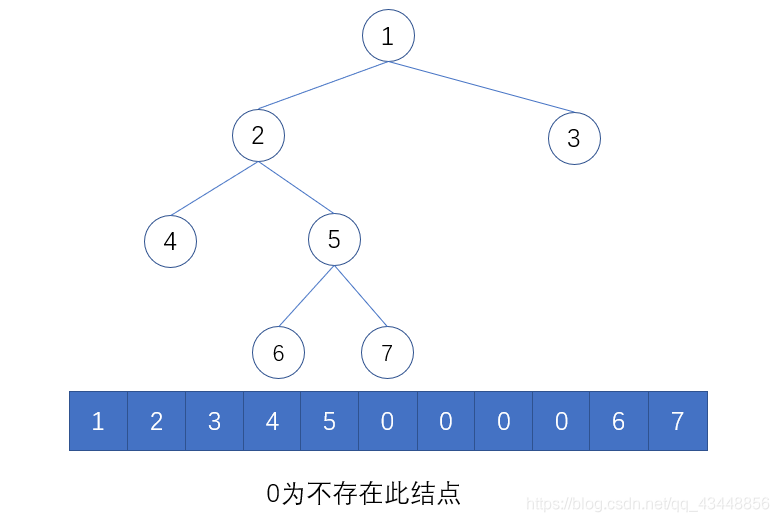
??按照顺序存储结构的定义,在此约定,用一组地址连续的存储单元依次自上而下、自左至右存储完全二叉树上的结点元素,即将完全二叉树上编号为 i 的结点元素存储在定义的一维数组中下标为 i-1 的分量中。
?
?
链式存储结构
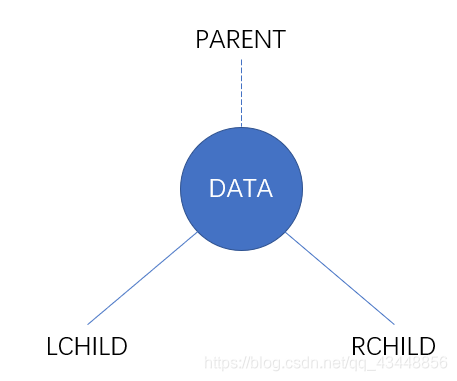
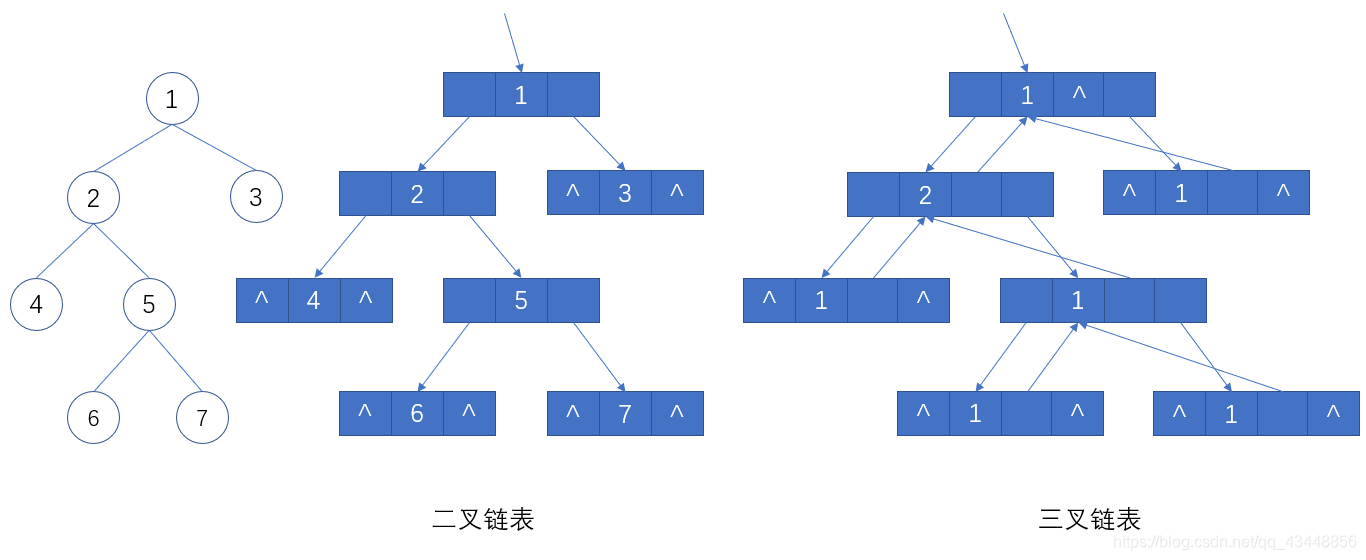
??二叉树的结点(如上图),由一个数据元素和分别指向其左、右子树的两个分支构成,则表示二叉树的链表中的结点至少包含 3 个域:数据域和左、右指针域,如下图所示。二叉链表

??有时,为了便于找到结点的双亲,则还可以在结点结构中增加一个指向其双亲结点的指针域,如下图所示。三叉链表

??在含有 n 个结点的二叉链表中有 n+1 个空链域。
二叉链表定义:
typedef struct BiTNode {
TElemType data;
struct BiTNode *lchild, *rchild;//左右孩子指针
}BiTNode, *BiTree;
?
?
遍历二叉树
遍历二叉树: 如何按某条搜索路径巡访树的每个结点,使得每个结点均被访问一次,而且仅被访问一次。“访问”的含义很广,可以是对结点作各种处理,如输出结点的信息等。
?
二叉树建立
不管是先序、中序、后序建树,输入的序列都应为先序。
先序建树
void PreorderBiTree(BiTree &T){//先序建立二叉树
char a;
scanf("%c",&a);
if(a == '#'){
T = NULL;
}
else{
T = (BiTree)malloc(sizeof(BiTNode));
if(!T){
printf("内存分配出现问题!!!\n");
printf("请重新启动程序!!!");
exit(0);
}
T->data = a;//将数据赋值给该节点
PreorderBiTree(T->lchild);//建立左孩子
//printf("%c ",T->data);
PreorderBiTree(T->rchild);//建立右孩子
}
}
中序建树
void InOrderBiTree(BiTree &T){//中序建立二叉树
char a;
scanf("%c",&a);
if(a == '#'){
T = NULL;
}
else{
T = (BiTree)malloc(sizeof(BiTNode));
if(!T){
printf("内存分配出现问题!!!\n");
printf("请重新启动程序!!!");
exit(0);
}
InOrderBiTree(T->lchild);//建立左孩子
T->data = a;//将数据赋值给该节点
//printf("%c ",T->data);
InOrderBiTree(T->rchild);//建立右孩子
}
}
后序建树
void PostorderBiTree(BiTree &T){//后序建立二叉树
char a;
scanf("%c",&a);
if(a == '#'){
T = NULL;
}
else{
T = (BiTree)malloc(sizeof(BiTNode));
if(!T){
printf("内存分配出现问题!!!\n");
printf("请重新启动程序!!!");
exit(0);
}
PostorderBiTree(T->lchild);//建立左孩子
PostorderBiTree(T->rchild);//建立右孩子
T->data = a;//将数据赋值给该节点
}
}
?
递归算法
先序遍历(中左右)
先序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则:
(1)访问根结点;
(2)先序遍历左子树;
(3)先序遍历右子树。
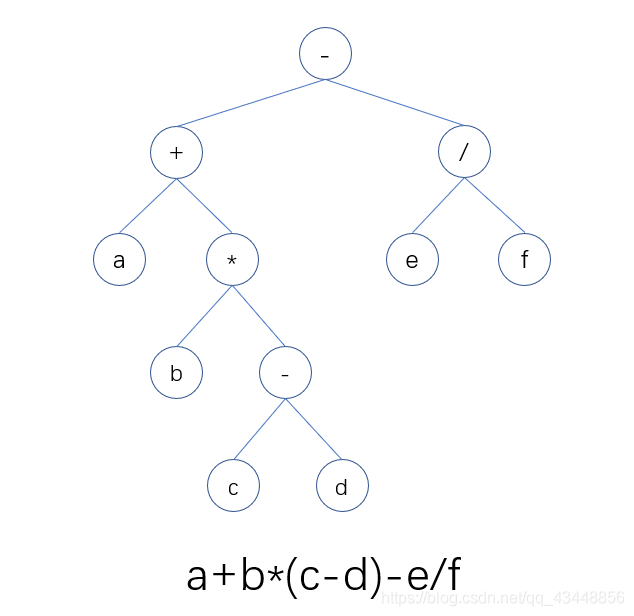
遍历顺序:-+a*b-cd/ef(波兰式)
void PreorderTraverse(BiTree T){//先序遍历输出
if(T){
PrintElement(T->data);//输出data
PreorderTraverse(T->lchild);
PreorderTraverse(T->rchild);
}
return;
}
?
中序遍历(左中右)
中序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则:
(1)先序遍历左子树;
(2)访问根结点;
(3)先序遍历右子树。
遍历顺序:a+b*c-d-e/f(逆波兰式)
void InOrderTraverse(BiTree T){//中序遍历输出
if(T){
InOrderTraverse(T->lchild);
PrintElement(T->data);//输出data
InOrderTraverse(T->rchild);
}
return;
}
?
后序遍历(左右中)
后序遍历二叉树的操作定义:
若二叉树为空,则空操作;否则:
(1)先序遍历左子树;
(2)先序遍历右子树;
(3)访问根结点。
遍历顺序:abcd-*+ef/-(逆波兰式)
void PostorderTraverse(BiTree T){//后序遍历输出
if(T){
PostorderTraverse(T->lchild);
PostorderTraverse(T->rchild);
PrintElement(T->data);//输出data
}
return;
}
?
非递归算法
先序遍历(中左右)
(1)访问结点P,并将结点P入栈;
(2)判断结点P的左孩子是否为空,若为空,则取栈顶结点并进行出栈操作,并将栈顶结点的右孩子置为当前的结点P,循环至(1);若不为空,则将P的左孩子置为当前的结点P;
(3)直到P为NULL并且栈为空,则遍历结束。
void PreorderTraverse(BiTree T){//先序遍历(非递归)
BiTree S[1000];//栈
int top = 0;//栈顶标记
BiTree e = T;
if(!e){
return;
}
while(e || top > 0){
while(e){
printf("%c",e->data);//访问结点
S[top++] = e;//入栈
e = e->lchild;
}
e = S[top-1];//返回栈顶
top--; //出栈
e = e->rchild;
}
}
?
中序遍历(左中右)
(1)若其左孩子不为空,则将P入栈并将P的左孩子置为当前的P,然后对当前结点P再进行相同的处理;
(2)若其左孩子为空,则取栈顶元素并进行出栈操作,访问该栈顶结点,然后将当前的P置为栈顶结点的右孩子;
(3)直到P为NULL并且栈为空则遍历结束。
void InOrderTraverse(BiTree T){//中序遍历(非递归)
BiTree S[1000];//栈
int top = 0;//栈顶标记
BiTree e = T;
if(!e){
return;
}
while(e || top > 0){
while(e){
S[top++] = e;
e = e->lchild;
}
e = S[top-1];
top--;
printf("%c",e->data);//访问结点
e = e->rchild;
}
}
?
后序遍历(左右中)
对于一个节点而言,要实现访问顺序为左儿子-右儿子-根节点,
可以利用后进先出的栈,在节点不为空的前提下,依次将根节点,右儿子,左儿子压栈。
故我们需要按照根节点-右儿子-左儿子的顺序遍历树,
而我们已经知道先序遍历的顺序是根节点-左儿子-右儿子,
故只需将先序遍历的左右调换并把访问方式打印改为压入另一个栈即可。
最后一起打印栈中的元素。
void PostorderTraverse1(BiTree T){//后序遍历(非递归)
BiTree S[1000];//栈
BiTree H[1000];
int tops = 0,toph = 0;
BiTree e = T;//f为标记
if(!e){
return;
}
while(e || tops > 0){
while(e){
S[tops++] = e;
H[toph++] = e;
e = e->rchild;
}
e = S[tops - 1];
tops--;
e = e->lchild;
}
while(toph > 0){
printf("%c",H[toph - 1]->data);
toph--;
}
}
要访问一个节点的条件上一个访问的节点是右儿子。我们可以增加一个变量Prev来判断当前节点Curr的上一个节点与它的关系来执行相应的操作。
若Prev为空(Curr节点是根节点)或者Prev是Curr的父节点,将Curr节点的左孩子和右孩子分别压入栈;
若Prev是Curr的左儿子,则将Curr的右儿子压入栈;
否则Prev是Curr的右儿子,访问Curr;
void PostorderTraverse2(BiTree T){//后序遍历(非递归)
BiTree S[1000];//栈
int top = 0;
S[top++] = T;
BiTree e = NULL,f = NULL;
while(top > 0){
e = S[top-1];
if(f == NULL || f->lchild == e || f->rchild == e){
if(e->lchild)
S[top++] = e->lchild;
else if(e->rchild)
S[top++] = e->rchild;
}
else if(e->lchild == f){
if(e->rchild)
S[top++] = e->rchild;
}
else{
printf("%c",e->data);
top--;
}
f = e;
}
}
?
?