目录
一.哈夫曼树
1.什么是哈夫曼树?
哈夫曼树:给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman Tree)。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
2.哈夫曼树关键字说明
- 路径和路径长度:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为 1,则从根结点到第 L 层结点的路径长度为 L-1。
- 结点的权及带权路径长度:若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结 点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积
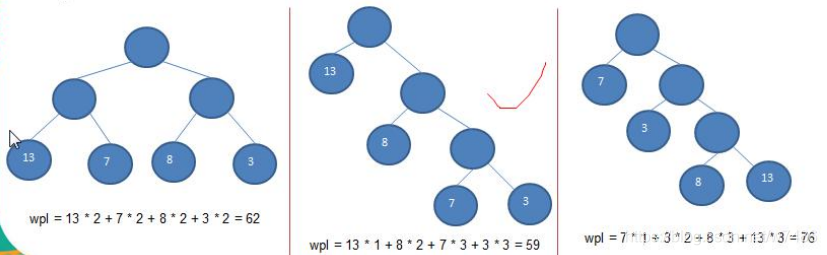
- 树的带权路径长度:树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为 WPL(weighted path length) ,权值越大的结点离根结点越近的二叉树才是最优二叉树。
- ?WPL 最小的就是赫夫曼树
3.用代码实现哈夫曼树思路分析
例如:给你一个数列 {13, 7, 8, 3, 29, 6, 1},要求转成一颗哈夫曼树
思路分析:
- 从小到大进行排序, 将每一个数据,每个数据都是一个节点 , 每个节点可以看成是一颗最简单的二叉树
- 取出根节点权值最小的两颗二叉树
- 组成一颗新的二叉树, 该新的二叉树的根节点的权值是前面两颗二叉树根节点权值的和
- 再将这颗新的二叉树,以根节点的权值大小 再次排序, 不断重复 1-2-3-4 的步骤,直到数列中,所有的数据都被处理,就得到一棵哈夫曼树

4.代码实现?
package com.ws.HuffMan;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
public class HuffmanTree {
/**
* 创建哈夫曼树
* @param arr 要变成哈夫曼树的数组
* @return 哈夫曼树的root节点
*/
public Node creatHuffMan(int[] arr) {
//创建一个node集合
List<Node> nodes = new ArrayList<Node>();
//把数组中的数传入集合
for (int value : arr) {
nodes.add(new Node(value));
}
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//取集合前两个最小的 创建一个二叉树
Node parent = new Node(leftNode.value + rightNode.value);
parent.left = leftNode;
parent.right = rightNode;
//再把集合中前两个删除
nodes.remove(0);
nodes.remove(0);
// nodes.remove(leftNode);
// nodes.remove(rightNode);
//再把新建二叉树的父节点传入集合
nodes.add(parent);
}
return nodes.get(0);
}
/**
* 前序遍历
* @param root
*/
public void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("空树~");
}
}
}
class Node implements Comparable<Node>{
//权值
public int value;
public Node left;
public Node right;
public Node(int value) {
this.value = value;
}
@Override
public int compareTo(Node o) {
//从小到大
return this.value - o.value;
}
//写一个前序遍历
public void preOrder() {
//先输出当前节点
System.out.print(this.value + " ");
//左遍历
if (this.left != null) {
this.left.preOrder();
}
//右遍历
if (this.right != null) {
this.right.preOrder();
}
}
}
?测试代码:
public static void main(String[] args) {
int[] arr = {13, 7, 8, 3, 29, 6, 1};
//创建哈夫曼对象
HuffmanTree huffmanTree = new HuffmanTree();
//传入数组创建哈夫曼树 得到哈夫曼树的root节点
Node root = huffmanTree.creatHuffMan(arr);
//根据root节点前序遍历
huffmanTree.preOrder(root);
}?输出结果:
67 ?29 ?38 ?15 ?7 ?8 ?23 ?10 ?4 ?1 ?3 ?6 ?13 ?
?就是前面思路分析中得到的哈夫曼树的前序遍历
二.哈夫曼编码
1.哈夫曼编码基本介绍
- 哈夫曼编码(Huffman Coding),又称霍夫曼编码,是一种编码方式, 属于一种程序算法
- 哈夫曼编码是赫哈夫曼树在电讯通信中的经典的应用之一。
- 哈夫曼编码广泛地用于数据文件压缩。其压缩率通常在 20%~90%之间
- 哈夫曼码是可变字长编码(VLC)的一种。Huffman 于 1952 年提出一种编码方法,称之为最佳编码
2.原理剖析
2.1.通信领域中信息的处理方式 1-定长编码
?2.2.哈夫曼编码方式处理
- i like like like java do you like a java
- d:1 ???y:1? ? u:1? ? j:2? ? v:2? ? o:2? ? l:4? ? k:4? ? ?e:4 ???i:5? ? ?a:5? ? ?' ':9 // 各个字符对应的个数
- 按照上面字符出现的次数构建一颗赫夫曼树, 次数作为权值
实现哈夫曼编码步骤:
- 把次数当作权值创建二叉
 ?
? - 向左为0,向右为1得到每个字符得哈夫曼编码? ?
-
o: 1000u: 10010d: 100110y: 100111i: 101a : 110k: 1110e: 1111j: 0000v: 0001l: 001' ': 01
- 按照上面的赫夫曼编码,我们的"i like like like java do you like a java" 字符串对应的编码为 (注 意这里我们使用的无损压缩) 10101001101111011110100110111101111010011011110111101000011000011100110011110000110 01111000100100100110111101111011100100001100001110
- 通过赫夫曼编码处理长度为 133.
说明:
原来长度是 359 , 压缩了 (359-133)?/ 359 = 62.9%
此编码满足前缀编码
,
即字符的编码都不能是其他字符编码的前缀。不会造成匹配的多义性
哈夫曼编码是无损处理方案?
3.代码实现
package com.ws;
import java.util.*;
public class HuffmanCode {
//存放哈夫曼编码的map 例如 a:10 b:1001 c:1000
static Map<Byte, String> huffmanCodeMap = new HashMap<>();
static StringBuilder code = new StringBuilder();
/**
* 重载getHuffManCode方法 这样只需要传入一个根节点参数就能得到哈夫曼编码了
* @param node
* @return
*/
public static Map<Byte, String> getHuffmanCode(Node node) {
if (node != null) {
return getHuffmanCode(node,"",code);
} else {
return null;
}
}
/**
* 将赫夫曼树的叶子节点 转换成赫夫曼编码 放再map中
*规定向左为0 向右为1
* @param node 节点
* @param s 0 or 1
* @param code 赫夫曼编码
* @return 存放哈夫曼编码的map 例如 a:10 b:1001 c:1000
*/
public static Map<Byte, String> getHuffmanCode(Node node, String s, StringBuilder code) {
StringBuilder stringBuilder = new StringBuilder(code);
stringBuilder.append(s);
if (node != null) {
if (node.data == null) {
//node.data == null 说明该节点不是叶子节点
//向左
getHuffmanCode(node.left, "0", stringBuilder);
//向右
getHuffmanCode(node.right, "1", stringBuilder);
} else {
//说明该点是叶子节点 直接放到map中
huffmanCodeMap.put(node.data, stringBuilder.toString());
}
}
return huffmanCodeMap;
}
public static byte[] huffmanZip(String content) {
//将字符串转成Byte数组
byte[] contextBytes = content.getBytes();
//将byte数组转换形成 Node 以便创建哈夫曼树
List<Node> nodes = getNodeBytes(contextBytes);
//将node集合 转换成哈夫曼树
Node root = creatHuffManTree(nodes);
//将赫夫曼树的叶子节点 转换成赫夫曼编码 放再map中
Map<Byte, String> huffManCodeMap = getHuffmanCode(root);
// System.out.println(huffManCodeMap);
//遍历数组 得到完整的哈夫曼编码
StringBuilder huffmanCode = new StringBuilder();
for (byte b : contextBytes) {
huffmanCode.append(huffManCodeMap.get(b));
}
//将得到的字符串编码转成byte放到byte数组中
byte[] huffmanCodeBytes = new byte[(huffmanCode.length() + 7) / 8];
int index = 0;
for (int i = 0; i < huffmanCode.length(); i += 8) {
String s = "";
if (i + 8 < huffmanCode.length()) {
s = huffmanCode.substring(i, i + 8);
} else {
s = huffmanCode.substring(i);
}
//每8位转成byte放在byte数组中
huffmanCodeBytes[index] = (byte) Integer.parseInt(s, 2);
index++;
}
return huffmanCodeBytes;
}
// String context = "i like java do you like java too";
// byte[] contextBytes = context.getBytes();
/**
* 将byte数组 转换形成 Node 以便创建哈夫曼树
* 例如: betes = {a, a, b, b ,b} ==> node[data:a, weight:2] node[data:b, weight:3]
* @param bytes
* @return
*/
public static List<Node> getNodeBytes(byte[] bytes) {
//遍历bytes 用map接收 k代表字符 v代表出现次数 也就是权重
Map<Byte, Integer> map = new HashMap<Byte, Integer>();
for (byte b : bytes) {
Integer weight = map.get(b);
if (weight == null) {
//weight == null表示map里还没添加这个字符 也就是这个字符第一次出现
map.put(b, 1);
} else {
map.put(b, weight++);
}
}
//遍历map 把map中数据add到node集合中
//创建一个node集合
List<Node> nodes = new ArrayList<Node>();
for (Map.Entry<Byte, Integer> entry : map.entrySet()) {
nodes.add(new Node(entry.getKey(), entry.getValue()));
}
return nodes;
}
/**
* 创建哈夫曼树
* @param nodes 节点集合
* @return 哈夫曼树的根节点
*/
public static Node creatHuffManTree(List<Node> nodes) {
while (nodes.size() > 1) {
//排序
Collections.sort(nodes);
Node leftNode = nodes.get(0);
Node rightNode = nodes.get(1);
//取集合前两个最小的 创建一个二叉树
Node parent = new Node(null,leftNode.weight + rightNode.weight);
parent.left = leftNode;
parent.right = rightNode;
//再把集合中前两个删除
nodes.remove(0);
nodes.remove(0);
// nodes.remove(leftNode);
// nodes.remove(rightNode);
//再把新建二叉树的父节点传入集合
nodes.add(parent);
}
return nodes.get(0);
}
/**
* 前序遍历
* @param root
*/
public static void preOrder(Node root) {
if (root != null) {
root.preOrder();
} else {
System.out.println("空树~");
}
}
}
class Node implements Comparable<Node>{
//数据也就是字符本身'a'=>95 ' '=>32
public Byte data;
//权值
public int weight;
public Node left;
public Node right;
public Node(Byte data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
//从小到大
return this.weight - o.weight;
}
//写一个前序遍历
public void preOrder() {
//先输出当前节点
System.out.println(this);
//左遍历
if (this.left != null) {
this.left.preOrder();
}
//右遍历
if (this.right != null) {
this.right.preOrder();
}
}
@Override
public String toString() {
return "Node{" +
"data=" + data +
", weight=" + weight +
'}';
}
}
测试代码:
public class Test {
public static void main(String[] args) {
String content = "i like java do you like java too";
byte[] huffmanCodeBytes = HuffmanCode.huffmanZip(content);
System.out.println(HuffmanCode.huffmanCodeMap);
for (byte b : huffmanCodeBytes) {
System.out.print(b+" ");
}
}
}结果:
{32=0110, 97=0111, 100=1000, 101=1001, 105=1010, 106=1011, 107=1100, 108=1101, 111=1110, 116=1111, 117=000, 118=001, 121=010}
-90 ?-38 ?-55 ?107 ?114 ?-19 ?28 ?-53 ?-125 ?109 ?100 ?-75 ?-71 ?118 ?-2 ?14?
?