1.写在前面
前面我已经简单的介绍了HashMap的源码了,但是HashMap的源码,其中涉及到了链表的一些操作,我就选择了略过,没有进行特殊的介绍,这个时候我们需要介绍一下有关这方便的知识,也就是数组和链表的一些知识,为了方便大家看清楚之前的代码。
2.数组
数组是原来就有的数据格式,这种数据格式就是在内存中开辟一整串的内存的空间,同时原生的也是只能存一种类型,当我去向内存申请一串数组的时候,CPU先计算出来我们数组中存储的元素是什么?根据这个元素计算出它的长度,然后同时我们需要知道这个数组中要存储多少个元素,然后计算出来我们需要开辟的空间,这个空间是连续的,具体的如下:
数组的访问
int[] array = new int[5];
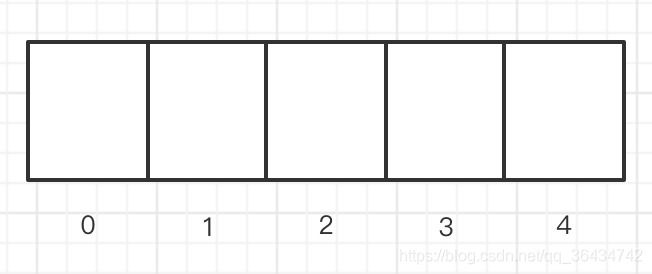
数组是一整串的连续的空间,然后我们可以通过下标的可以直接访问,这样就可以通过计算出来内存的位置,然后得出这个位置的值。
数组的插入
在数组的结尾后插入,假设原来的数组的内容如下:
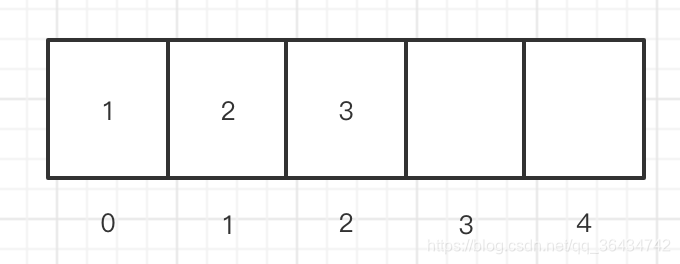
假如这个时候我们往数组的末尾的时候插入,具体的代码如下:
array[3] = 4
这个时候我们就不需要移位操作的,如果我们往数组的下标的2插入,这个时候内容就如下:
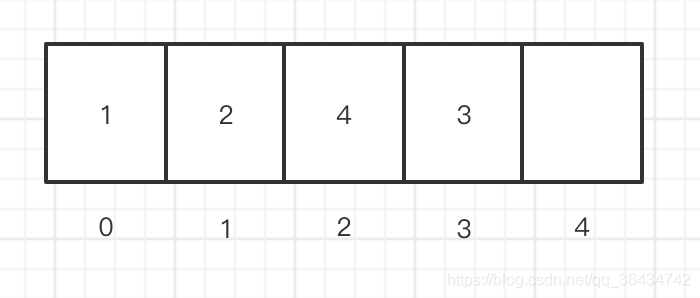
这个时候我们就需要移位的操作,具体的代码如下:
array[3] = array[2];
array[2] = 4;
如果是插入到更靠前的位置,我们就需要更多位的移位操作。
数组是删除
删除数组结尾的元素,具体的如下:
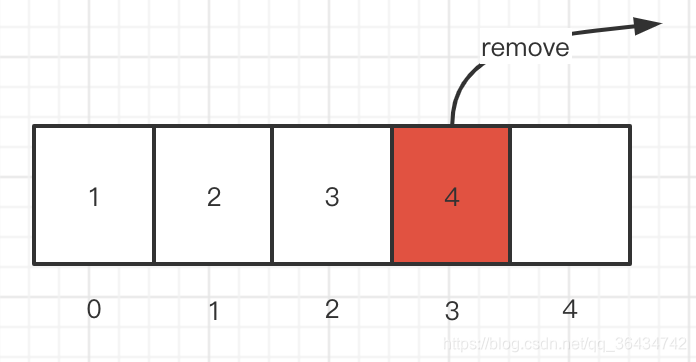
这个时候我们也不需要移位的操作,具体的代码如下;
array[3] = null;
删除的元素不在数组的结尾,具体的如下:
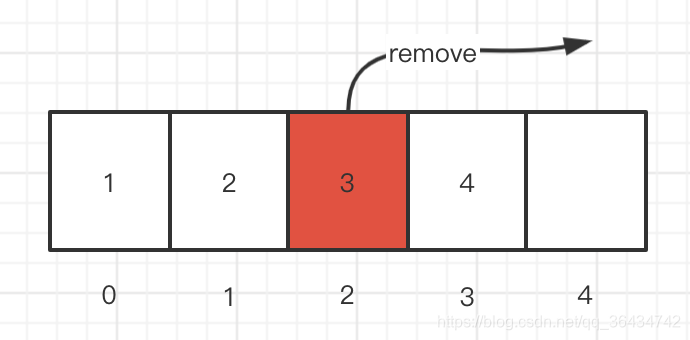
这个时候删除的元素就不在最后一位了,这个时候我们就需要移位操作,具体的代码如下:
array[3] = array[4];
array[4] = null;
3.链表
链表在原来数组的基础上,进行了对应修改,原来的数组是一整串的内存的空间,这样如果内存的碎片化比较严重,没有一个完整的内存的空间,这样就会导致开辟数组空间的时候出错,这个时候我们就需要一种新的数据结构,来针对这种内存碎片化的无法开辟完整的空间,这个时候就需要一种新的数据结构,就是我们的链表,具体的如下:
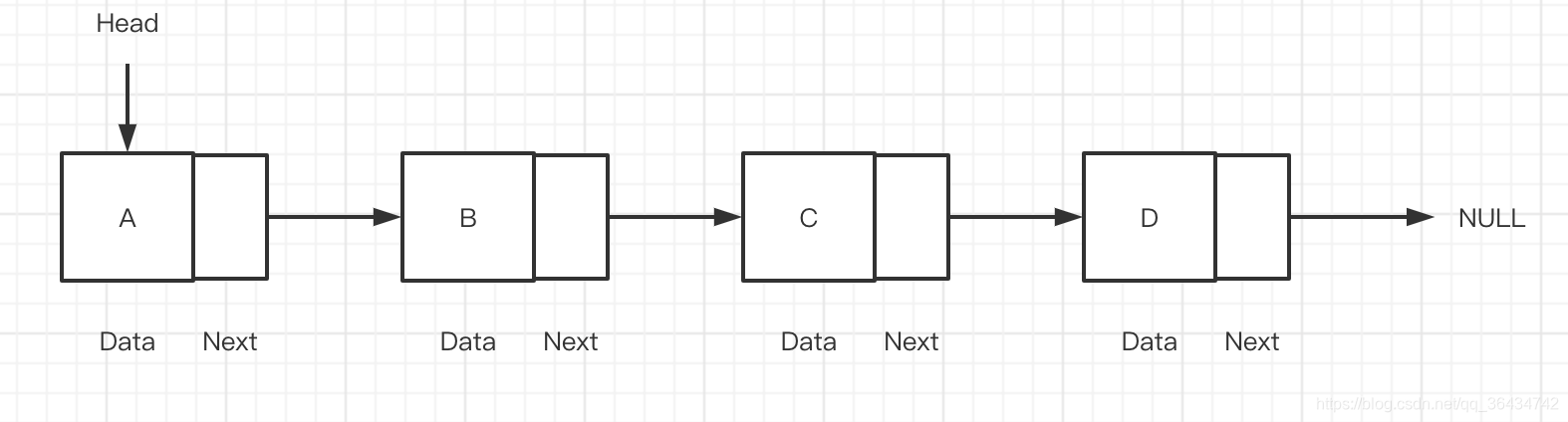
我们先看看简单的链表的类,Node表示链表中的节点。具体的如下:
class LinkedList {
Node head;
class Node {
int data;
Node next;
Node(int d) { data = d; }
}
}
创建和插入、遍历链表
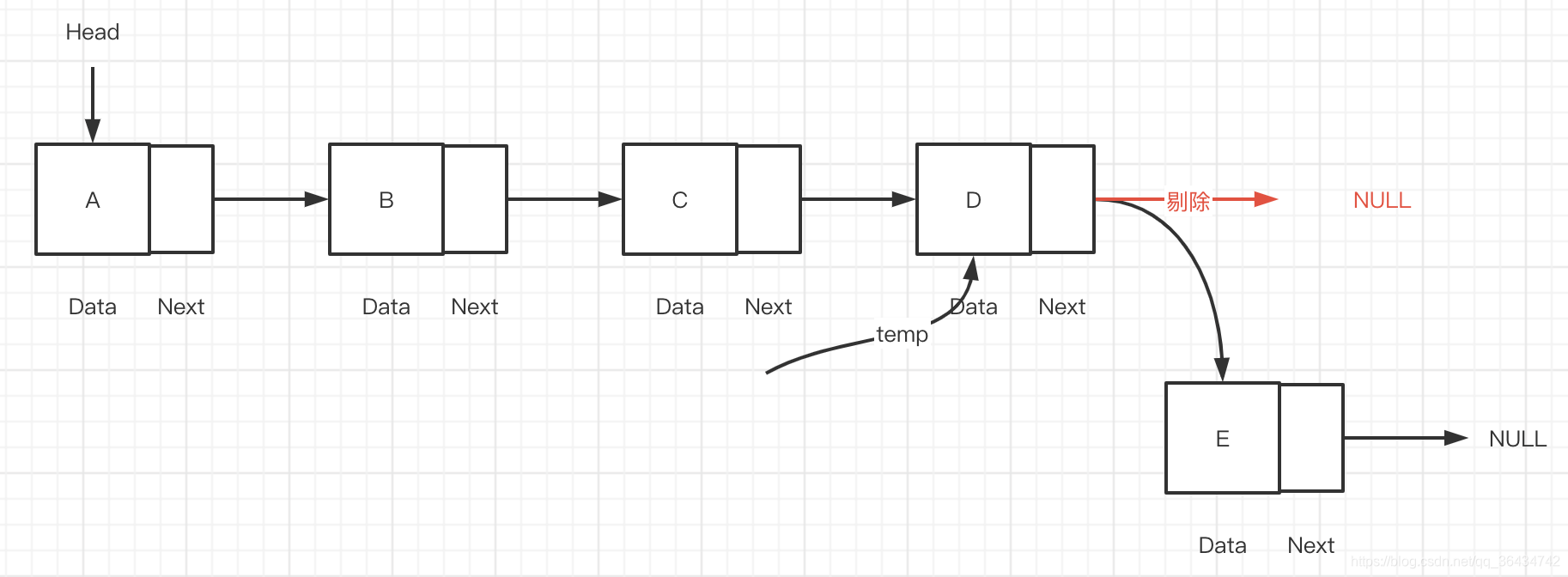
我们先来看下创建和插入的代码,具体的如下:
package com.ys;
public class LinkedList {
Node head;
static class Node {
int data;
Node next;
Node(int d) {
data = d;
next = null;
}
}
public static LinkedList insert(LinkedList list, int data) {
//先创建一个Node节点
Node new_node = new Node(data);
new_node.next = null;
//判断头节点是不是空
if (list.head == null) {
list.head = new_node;//将当前创建的节点设置为头节点
} else {
Node last = list.head;
//遍历这个链表,找到最后的一个节点
while (last.next != null) {
last = last.next;
}
//尾插法插入节点
last.next = new_node;
}
return list;
}
public static void printList(LinkedList list) {
Node currNode = list.head;
System.out.print("LinkedList: ");
while (currNode != null) {
System.out.print(currNode.data + " ");
currNode = currNode.next;
}
}
public static void main(String[] args) {
LinkedList list = new LinkedList();
list = insert(list, 1);
list = insert(list, 2);
list = insert(list, 3);
list = insert(list, 4);
list = insert(list, 5);
list = insert(list, 6);
list = insert(list, 7);
list = insert(list, 8);
printList(list);
}
}
上面的就是尾插法的插入节点,可以参考我上面的图,就是用一个中间的变量然后找到最后一个节点,然后将最后一个节点的next设置为创建的节点。输出的结果如下:

根据值删除
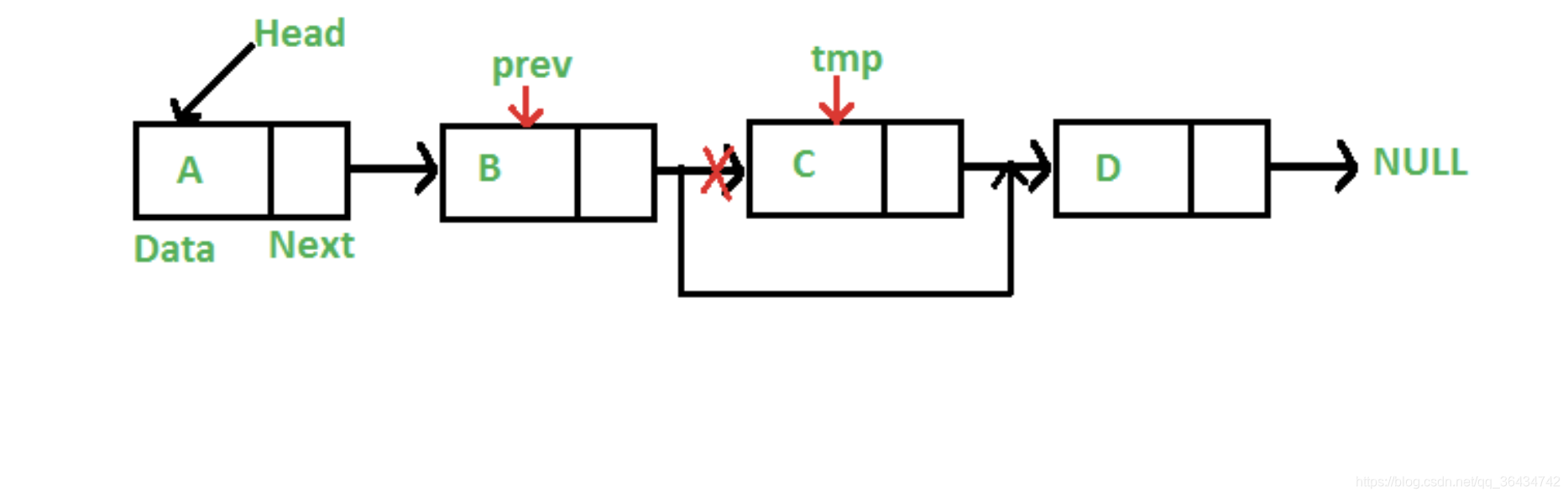
具体的代码如下:
package com.ys;
public class LinkedList {
Node head;
static class Node {
int data;
Node next;
Node(int d) {
data = d;
next = null;
}
}
public static LinkedList insert(LinkedList list,
int data) {
Node new_node = new Node(data);
new_node.next = null;
if (list.head == null) {
list.head = new_node;
} else {
Node last = list.head;
while (last.next != null) {
last = last.next;
}
last.next = new_node;
}
return list;
}
public static void printList(LinkedList list) {
Node currNode = list.head;
System.out.print("LinkedList: ");
while (currNode != null) {
System.out.print(currNode.data + " ");
currNode = currNode.next;
}
System.out.println();
}
public static LinkedList deleteByKey(LinkedList list,
int key) {
//先取出头节点
Node currNode = list.head, prev = null;
//判断头节点是否等于传入的key
if (currNode != null && currNode.data == key) {
//将头节点指向头节点的下一级节点
list.head = currNode.next;
System.out.println(key + " found and deleted");
//然后直接返回
return list;
}
//遍历当前链表,找到等于key的节点
while (currNode != null && currNode.data != key) {
// prev 等于要删除的节点上一级节点
prev = currNode;
//currNode 等于删除的节点的
currNode = currNode.next;
}
//如果要删除的节点不为空
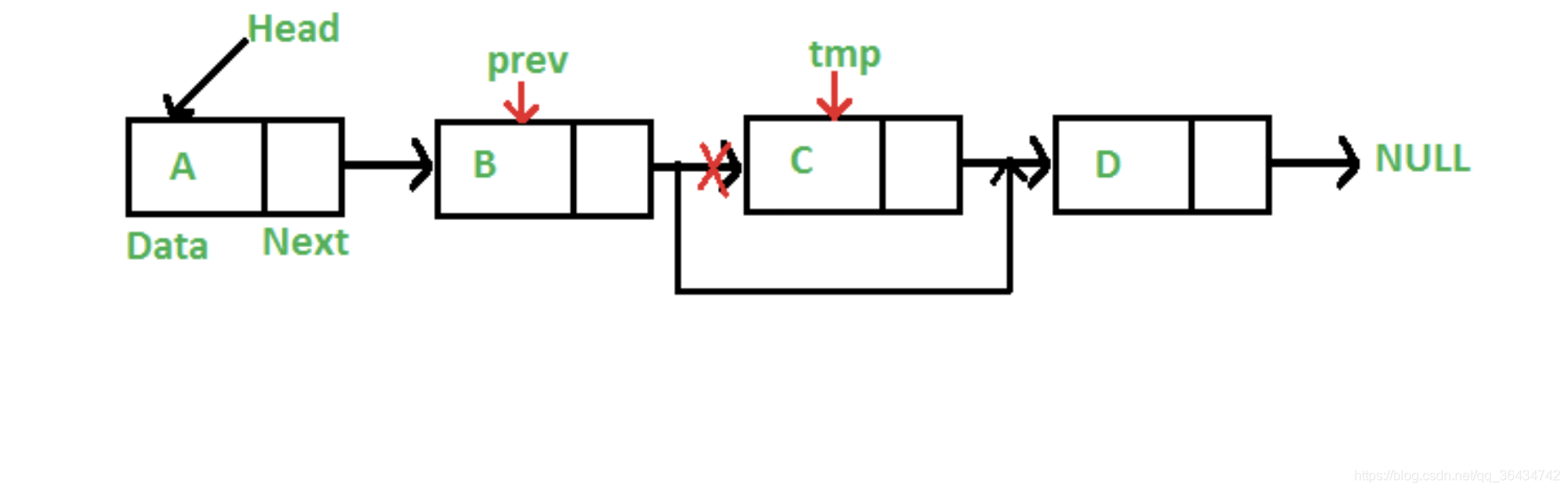
if (currNode != null) {
// 删除的节点的上一级节点的next指向删除的节点的next
prev.next = currNode.next;
System.out.println(key + " found and deleted");
}
//如果要删除的节点为null,表示要删除的节点没有找到
if (currNode == null) {
System.out.println(key + " not found");
}
return list;
}
public static void main(String[] args) {
LinkedList list = new LinkedList();
list = insert(list, 1);
list = insert(list, 2);
list = insert(list, 3);
list = insert(list, 4);
list = insert(list, 5);
list = insert(list, 6);
list = insert(list, 7);
list = insert(list, 8);
printList(list);
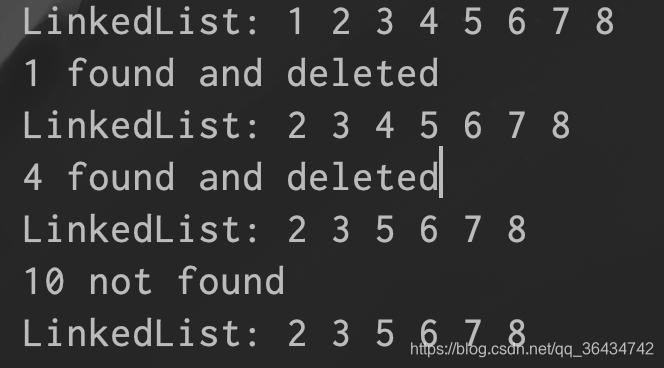
deleteByKey(list, 1);
printList(list);
deleteByKey(list, 4);
printList(list);
deleteByKey(list, 10);
printList(list);
}
}
上面根据传入key的删除节点,先判断头节点是不是我们要找的节点,如果是的,直接删除,然后遍历剩下的节点,然后prev指向要删除的节点的上一个节点,currNode是要删除的节点,如果要删除的节点不为空,然后就直接删除这个节点,如果这个currNode是为null,就表示要删除的节点没有找到。运行的结果如下:
根据位置删除
具体的代码如下:
package com.ys;
public class LinkedList {
Node head;
static class Node {
int data;
Node next;
Node(int d) {
data = d;
next = null;
}
}
public static LinkedList insert(LinkedList list,
int data) {
Node new_node = new Node(data);
new_node.next = null;
if (list.head == null) {
list.head = new_node;
} else {
Node last = list.head;
while (last.next != null) {
last = last.next;
}
last.next = new_node;
}
return list;
}
public static void printList(LinkedList list) {
Node currNode = list.head;
System.out.print("LinkedList: ");
while (currNode != null) {
System.out.print(currNode.data + " ");
currNode = currNode.next;
}
System.out.println();
}
public static LinkedList deleteAtPosition(LinkedList list, int index) {
Node currNode = list.head, prev = null;
//位置为0,同时当前的头节点不会空,直接删除头节点
if (index == 0 && currNode != null) {
list.head = currNode.next;
System.out.println(index + " position element deleted");
return list;
}
//位置
int counter = 0;
while (currNode != null) {
//如果位置等于传入的位置,直接删除节点
if (counter == index) {
prev.next = currNode.next;
System.out.println(index + " position element deleted");
break;
} else {
//prev 等于要删除的节点的上一个节点
prev = currNode;
//currNode 等于要删除的节点
currNode = currNode.next;
//位置++
counter++;
}
}
//如果要删除的节点为空的时候,表示删除的节点的为空
if (currNode == null) {
System.out.println(index + " position element not found");
}
return list;
}
public static void main(String[] args) {
LinkedList list = new LinkedList();
list = insert(list, 1);
list = insert(list, 2);
list = insert(list, 3);
list = insert(list, 4);
list = insert(list, 5);
list = insert(list, 6);
list = insert(list, 7);
list = insert(list, 8);
printList(list);
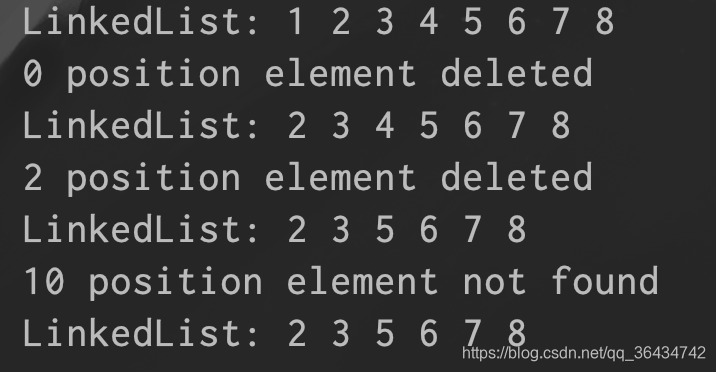
deleteAtPosition(list, 0);
printList(list);
deleteAtPosition(list, 2);
printList(list);
deleteAtPosition(list, 10);
printList(list);
}
}
上面根据传入index的位置删除节点,先判断index是不是等于0,如果是的,直接删除头节点,然后遍历剩下的节点,找到对应的位置,然后prev指向要删除的节点的上一个节点,currNode是要删除的节点,如果要删除的节点不为空,然后就直接删除这个节点,如果这个currNode是为null,就表示要删除的节点没有找到。运行的结果如下:
4.时间复杂度
数组的时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| prepend | O(1) |
| append | O(1) |
| lookup | O(1) |
| insert | O(n) |
| delete | O(n) |
链表的时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| prepend | O(1) |
| append | O(1) |
| lookup | O(n) |
| insert | O(1) |
| delete | O(1) |
5.跳表
看了上面的两种数据结构的时间复杂度,我们发现链表中只有随机访问是O(n),其他的都是O(1),那么我们能不能在此基础上进行优化一下,这样就有一种好的数据结构,那么有没有呢?当然有,就是跳表,我们大学的课本上是没有介绍,面试也不会问到,但是我们还是要了解这种的数据结构,因为这种数据结构是Redis的底层的数据结构。
那么如何提高链表的随机的访问的速度呢?链表是一维的结构,我们通过添加了头指针和尾指针,提高了访问头部和尾部的访问速度,那么我们可不可以通过添加多个节点来提高访问的速度。具体的如下:

我们可以通过空间换速度,给原始链表加上一个一级索引,这样就能提高随机访问的速度了。可能一级索引的速度只有一次走两步,可能对我们的速度提升不够明显,那么我们可以再加一级索引,具体的如下:
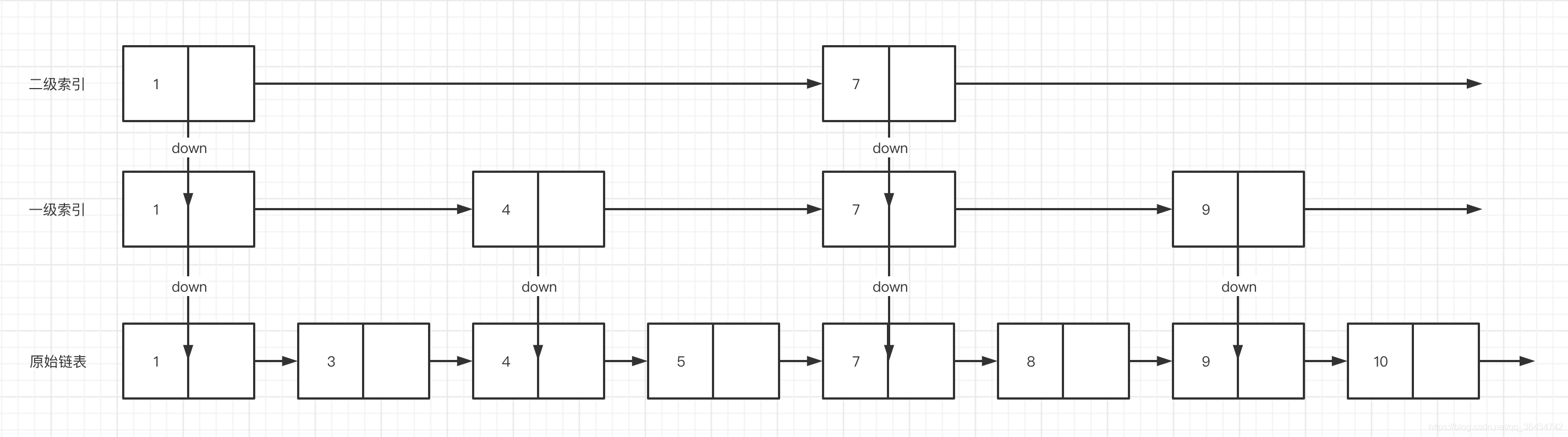
这样我们又升了一级维度,这样的访问速度又加快了。
依次类推,在现实的生活我们可以通过添加多级索引的方式来访问链表。那么增加多少个索引呢?其实增加log2n个级索引
时间复杂度分析
n/2、n/4、n/8、第K级索引结点的个数就是n/(k2),假设索引有h级,最高级的索引有2个结点。n/(h2) = 2,从而得到h=log2(n)-1。所以得出跳表的随机访问的元素的时间复杂度是O(logn)
跳表的时间复杂度
| 操作 | 时间复杂度 |
|---|---|
| prepend | O(logn) |
| append | O(logn) |
| lookup | O(logn) |
| insert | O(logn) |
| delete | O(logn) |
6.写在最后
本篇博客主要简单的介绍了下数组、链表、跳表等数据结构,同时介绍这几种数据结构的优点和缺点,同时也提及到数据结构中一个很重要的思想,升维的思想,空间换时间。