摘要

接上一讲的线性表，这讲针对单链表对线性表的缺点和单链表的优缺点、怎么理解单链表的操作做一个笔记，如果对线性表有疑问的可以看第一讲：第一讲线性表

线性表的链式存储结构绪论

线性表的顺序存储结构问题，使得线性表不能高效的进行数据的增删操作，因此提出了线性表的链式存储结构。关于线性表的链式存储结构可以在一定程度认为用空间换取对线性表的增删等工作的操作时间，对于这句话的解释说明，放在了总结里面。
先看线性表链式存储的结构：
为了表示每个数据元素 $a_i$ 与其直接后继元素 $a_( i+1_)$ 之间的逻辑关系，对数据元素 $a_i$ 而言，除了存储本身的信息之外，还需要存储表示后继元素的信息，把存储数据元素的空间称为数据域，把存储后继元素位置的空间称为指针域-----《大话数据结构》指针域存储的信息称为指针（本身就是指针）或者链，数据域和存储下一个后继元素的位置信息的指针域称为结点。
简单理解：
顺序存储结构就一个存储数据信息的地方，后继元素是紧挨着先驱元素（排除第一个元素和最后一元素，因为第一个元素没有先驱，最后一个元素没有后继），而链式存储结构中先驱结点中不仅有存储数据域还有存储后继结点位置的指针域。
注意：
顺序存储结构把线性表中相邻位置的元素（这里的元素不包括先驱和后继）称为先驱元素或者后继元素，链式存储结构则称为结点（这里指的节点不包括头和尾），同时要注意结点中的指针域存储的是下一个结点的位置，如下图示例所示：

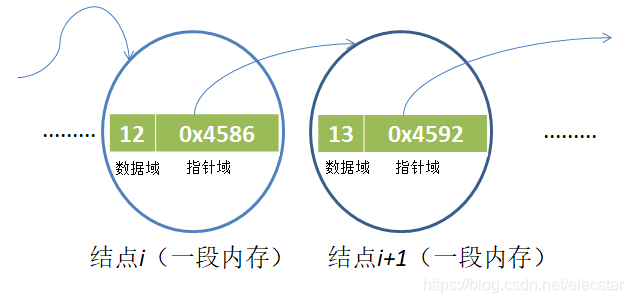
其中数据域存储的是该节点的数据信息，指针域存储的是下一个结点的指针，例如结点i的指针域[0x4586]存储的就是结点i+1的地址，结点i的指针域存储的是下一个结点的内存地址，该内存里面包含了该结点的数据信息的数据域和下一个结点内存的地址的指针域。下面对链式存储结构做一个补充：

单链表 ：n个结点链接成一个链表，类似于线性表的链式存储结构，因为每个结点只包含一个指针域，所以叫做单链表；
头结点：与第一个节点不同，头结点的指针域（头指针）存储了第一个结点的地址，其数据域可以存储线性表的长度等信息；
空链表：第一个结点的指针域存储的为“NULL”或“^”；
单链表存储结构：

typedef struct Node
{
	ElemType data;
	struct Node *next;
}Node;
typedef struct Node *LinkList

单链表的常规操作

这里与线性表类似，但是又不一样，这里需要理解指针，内存之间的关系。否则在进行插入和删除操作时不能理解。

单链表查找

查找第 $i$ 个数据

声明一个结点 $p$ 指向链表的第一个结点，申明一个计数变量 $j$ ；
当 $j < i$ 时，遍历链表，结点 $p$ 向后移动， $j$ 累加；
如果遍历到末尾结点，则说明第 $i$ 个元素不存在；
否则查找成功，返回 $p$ 的数据域。
伪代码：

Status GetElem(LinkList L, int i, ElemType *e)
{
	int j
	LinkList p;
	p = L -> next;
	j = 1;
	while(p && j< i) /*遍历链表*/
	{
		p = p -> next; /*获取下一个结点的地址*/
		++j; /*遍历计数*/
	}
	if !p || j>=i
		return error; /*链表中不存在i个元素*/
	*e = p->data; /*否则返回p的数据域*/
	return *e;
}

单链表就的遍历时间复杂度为 $O (n)$ 主要是遍历到第 $i$ 个元素，因为 $i = 1$ 和 $i = n$ 即最后一个，这是事前无法预料的，因此时间复杂度为 $O (n)$ ，其实是 $\frac{n+1}{2})$

单链表插入

在第 $i$ 个位置插入元素操作步骤

声明一个结点 $p$ 指向链表的第一个结点，申明一个计数变量 $j$ ；
当 $j < i$ 时，遍历链表，结点 $p$ 向后移动， $j$ 累加；
如果遍历到末尾结点，则说明第 $i$ 个元素不存在；
否则查找成功，向系统申请一个LinkList类型的结点 $s$ ；
将待插入的元素赋值给 $s$ 结点的数据域；
插入标准语句：s->next = p->next; p->next = s
返回
伪代码：

Status ListInsert(LinkList *L, int i,ElemType e)
{
	int j =1 ;
	LinkList p,s;
	p = *L; /*单链表的头结点地址赋值给p*/
	while(p && j<i) /*遍历*/
	{
		p = p -> next;
		++j;
	}
	if(!p || j>=i)     /*判断i个位置是否在链表中存在*/
		return error;
	s = (LinkList) malloc(sizeof(Node)); /*申请一块类型为LinkList，大小为sizeof(Node)的内存*/
	s -> data = e; /*把待插入数据放入s结点的数据域*/
	s -> next = p -> next;   /*将p结点的指针域赋值给s结点的指针域*/
	p -> next = s;         /*将s的地址赋值给p的指针域（后继）*/
	return e;
}

这里的第六点，s->next = p->next; p->next = s 需要解释一下，最开始我也有点没看懂，但是仔细思考了指针和内存的关系链表中指针域和结点的关系之后再看这个就醍醐灌顶了。
申请的s结点内存数据格式跟链表的数据格式是一致的，首先把待插入的数据赋值到s -> data然后把p结点(第i个位置插入)的指针域赋值给s->next这样s结点的指针域就指向了原本p结点指针域指向的下一个结点。再把s结点的地址赋值给p->next这样使得p的指针域指向的是s结点。

单链表删除

在第 $i$ 个位置删除元素操作步骤

声明一个结点 $p$ 指向链表的第一个结点，申明一个计数变量 $j$ ；
当 $j < i$ 时，遍历链表，结点 $p$ 向后移动， $j$ 累加；
如果遍历到末尾结点，则说明第 $i$ 个元素不存在；
否则查找成功，向系统申请释放结点 $p$ ；
将待删除的结点p->next赋值给 $q$ 结点；
删除的标准语句p->next = q -> next；
释放；
返回；
伪代码：

Status ListDelete(LinkList *L, int i, ElemType e)
{
	
	int j
	LinkList p,q;
	p = L -> next;
	j = 1;
	while(p && j< i) /*遍历链表*/
	{
		p = p -> next; /*获取下一个结点的地址*/
		++j; /*遍历计数*/
	}
	if(!p || j>=i)     /*判断i个位置是否在链表中存在*/
		return error ;
	q = p->next;
	p->next = q->next;
	e = q ->data;
	free(q);
	return e;
}