[数据结构与算法]最小生成树:Kruskal算法

最小生成树:Kruskal算法

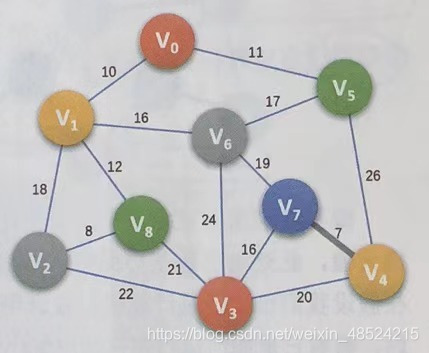
Kruskal算法的思想就是站在上帝视角,把整个图中权值最短的边一个个挑出来.

顶点数组

辅助数组(此数组旨在避免在构造最小生成树时产生回路)
$Vexset[i]$ :标识各个顶点所属的连通分量.表示该顶点所在的连通分量
$Vexset[i]=i$ :开始时每个顶点都自成一个连通分量
辅助数组的初始值:
V e x s e t [ i ] = { 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 } Vexset[i]=\{0,1,2,3,4,5,6,7,8\} Vexset[i]={0,1,2,3,4,5,6,7,8}

边集数组
$Edge[i]$:存储边的顶点下标和权值

typedef struct{
	VerTexType begin;	//边的始点下标
	VerTexType end;		//边的终点下标
	ArcType weight;		//边的权值
}Edge[arcnum];

将邻接矩阵通过程序转化为边集数组,并按权值从小到大排序

找出整个图中权值最小的边 $(V_4,V_7)$

至此连通分量有:
$V_4$ , $V_7$ 构成的一个连通分量
其余每个顶点都依旧各自自成一个连通分量

找出目前权值最小的边 $(V_2,V_8)$

至此连通分量有:
$V_2$ , $V_8$ 构成的一个连通分量
$V_4$ , $V_7$ 构成的一个连通分量
其余每个顶点都依旧各自自成一个连通分量

找出目前权值最小的边 $(V_0,V_1)$

至此连通分量有:
$V_0$ , $V_1$ 构成的一个连通分量
$V_2$ , $V_8$ 构成的一个连通分量
$V_4$ , $V_7$ 构成的一个连通分量
其余每个顶点都依旧各自自成一个连通分量

找出目前权值最小的边 $(V_0,V_5)$

$V_0$ , $V_1$ 构成一个连通分量
$V_0$ , $V_5$ 构成一个连通分量
因为边$(V_0,V_1)$ 和 边$(V_0,V_5)$ 中都有 $V_0$ 所以两个连通分量: 边$(V_0,V_1)$ 和 边$(V_0,V_5)$合并为一个连通分量

至此连通分量有:
$V_0$ $V_1$ $V_5$ 构成的一个连通分量
$V_2$ , $V_8$ 构成的一个连通分量
$V_4$ , $V_7$ 构成的一个连通分量
其余每个顶点都依旧各自自成一个连通分量

找出目前权值最小的边 $(V_1,V_8)$

$V_0$, $V_1$, $V_5$ 构成一个连通分量
$V_1$ , $V_8$ 构成一个连通分量
$V_2$ , $V_8$ 构成一个连通分量

因为连通分量 $V_0,V_1,V_5$ 和连通分量 $V_1,V_8$ 之间都有 $V_1$
因为连通分量 $V_1,V_8$ 和连通分量 $V_2,V_8$ 之间都有 $V_8$
以上所有连通分量合并为一个连通分量 $V_0,V_1,V_5,V_8,V_2$

至此连通分量有:
$V_0,V_1,V_5,V_8,V_2$ 构成的一个连通分量
$V_4$ , $V_7$ 构成的一个连通分量
其余每个顶点都依旧各自自成一个连通分量

找出目前权值最小的边 $(V_3,V_7)$

$V_4$ , $V_7$ 构成一个连通分量
$V_3$ , $V_7$ 构成一个连通分量
上述两个连通分量中都有 $V_7$ 所以将这两个连通分量合并为一个连通分量 $V_3,V_4,V_7$

至此连通分量有:
$V_0,V_1,V_5,V_8,V_2$ 构成的一个连通分量
$V_3$, $V_4$, $V_7$ 构成的一个连通分量
其余每个顶点都依旧各自自成一个连通分量

找出目前权值最小的边 $(V_1,V_6)$
$V_0,V_1,V_5,V_8,V_2$ 构成一个连通分量
$V_1,V_6$ 构成一个连通分量
以上两个连通分量中都有 $V_1$ 所以这两个连通分量合并成一个连通分量 $V_0,V_1,V_5,V_8,V_2,V_6$

至此连通分量有:
$V_0,V_1,V_5,V_8,V_2,V_6$ 构成的一个连通分量
$V_3$, $V_4$, $V_7$ 构成的一个连通分量

找出目前权值最小的边 $(V_6,V_7)$

$V_6,V_7$ 构成一个连通分量
$V_0,V_1,V_5,V_8,V_2,V_6$ 构成一个连通分量
$V_3$, $V_4$, $V_7$ 构成一个连通分量
以上三个连通分量由于 $V_6,V_7$ 而合并成一个连通分量 $V_0,V_1,V_5,V_8,V_2,V_6,V_7,V_3,V_4$

至此连通分量有:
$V_0,V_1,V_5,V_8,V_2,V_6,V_7,V_3,V_4$

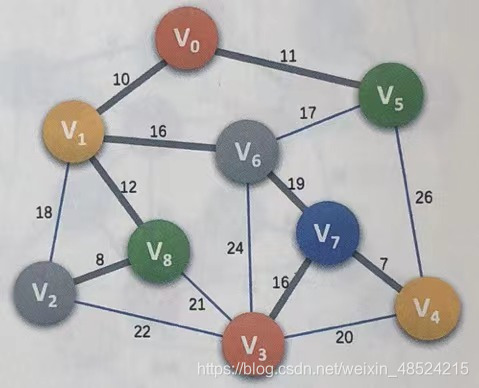
至此最小生成树构造完成

《数据结构C语言版》内的Kruskal算法描述

void MiniSpanTree_Kruskal(AMGraph G){
	Sort(Edge);	//按边的权值将边集数组元素从小到大排序
	for(i=0; i<G.vexnum; ++i)	//初始化辅助数组,各个顶点自成连通分量
		Vexset[i]=i;
	for(i=0; i<G.arcnum; ++i){
		v1=LocateVex(G,Edge[i].begin);	//边集数组中第i个元素中边的始点
		v2=LocateVex(G,Edge[i].end);	//边集数组中第i个元素中边的终点
		vs1=Vexset[v1];	//获取边Edge[i]的始点所在的连通分量
		vs2=Vexset[v2];	//获取边Edge[i]的终点所在的连通分量
		if(vs1 != vs2){	//边的两个顶点分属于不同的连通分量
			cout << Edge[i].begin << Edge[i].end;	//输出此边
			for(j=0; j<G.vexnum; ++j)	//合并vs1和vs2两个连通分量,即两个集合统一编号
				if(Vexset[j] == vs2)	//集合编号为vs2的都改为vs1
					Vexset[j]=vs1;		
		}
	}
}

《大话数据结构》内的Kruskal算法描述

void MiniSpanTree_Kruskal(MGraph){
	int i,n,m;
	Edge edges[MAXEDGE]; //定义边集数组
	int parent[MAXVEX];	 //定义数组parent来判断边与边是否形成环路（实质为并查集）
	Sort(edges);	//把边集数组中的边按权值从小到大排序
	for(i=0; i<G.numVertiexes; i++)	//初始化数组parent
		parent[i]=0;
	for(i=0; i<G.numEdges; i++){	//循环每一条边
		n = Find(parent,edges[i].begin); //边的始点下标
		m = Find(parent,edges[i].end);	//边的终点下标
		if(n != m){		//假如n不等于m，说明此边没有与现有的生成树形成环路
			parent[n]=m; //将此边的的终点放入parent中(此数组下标代表始点)表示此顶点已经在生成树集合中
			printf("(%d,%d) %d\n", edges[i].begin,edges[i].end,edges[i].weight);
		}
	}
}
//查找边的终点下标
int Find(int *parent, int f){
	while(parent[f] > 0){
		f = parent[f];
	}
	return f;
}