开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> javascript二叉树（二叉搜索树） -> 正文阅读

[数据结构与算法]javascript二叉树（二叉搜索树）

树

概念：

拥有相同的父节点的节点，互称为兄弟节点
节点的深度：从根节点到该节点所经历的边的个数
节点的高度：节点到叶节点的最长路径
树的高度：根节点的高度

二叉树

二叉树即最多仅有两个子节点的树

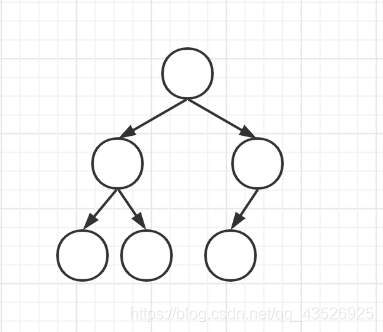
请添加图片描述

二叉树的存储方法：

链式存储（即用链表存储）
线性存储（即用数组存储）

二叉树常见类型

完全二叉树：如果对满二叉树的结点进行编号, 约定编号从根结点起, 自上而下, 自左而右。则深度为k的, 有n个结点的二叉树, 当且仅当其每一个结点都与深度为k的满二叉树中编号从1至n的结点一一对应时, 称之为完全二叉树。

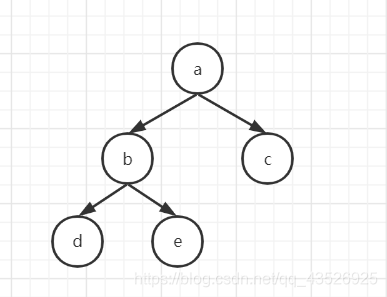
在这里插入图片描述

满二叉树：一棵深度为k且有（2的k次方 - 1）个结点的二叉树称为满二叉树。即除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树
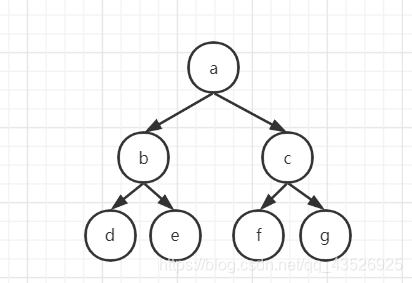
在这里插入图片描述

注意：满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

平衡二叉树：二叉树中，每一个节点的左右子树的高度相差不能大于 1，称为平衡二叉树。即上面两张都可以为平衡二叉树。

二叉搜索树(二叉排序树): 二叉搜索树具有以下性质：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树。

实现一棵二叉搜索树

function Tree(){
    //初始根节点为null
    this.root = null;
    //该构造函数为节点
    function Node(val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
    //该方法用于插入，传入的是值
    this.insert(val) {
        //需要将值转化为节点
        let newNode = new Node(val);
        if(this.root === null) {
            this.root = newNode;
        }else {
            insertNode(this.root, newNode);
        }
    }
    //该函数用于插入到节点里
    //这里的方法可以自己编写按照各种二叉树
    //我这是按照二叉搜索树概念进行
    function insertNode(node, newNode) {
		if(node.val > newNode.val) {
			if(node.left === null) {
				node.left = newNode;
			}else {
				insertNode(node.left, newNode);
			}
		}else {
			if(node.right === null) {
				node.right = newNode;
			}else {
				insertNode(node.right, newNode);
			}
		}
    }
}
//------------------进行测试
let a = new Tree();
a.insert(10);
a.insert(7);
a.insert(11);
a.insert(5);
a.insert(6);
a.insert(8);
a.insert(12);
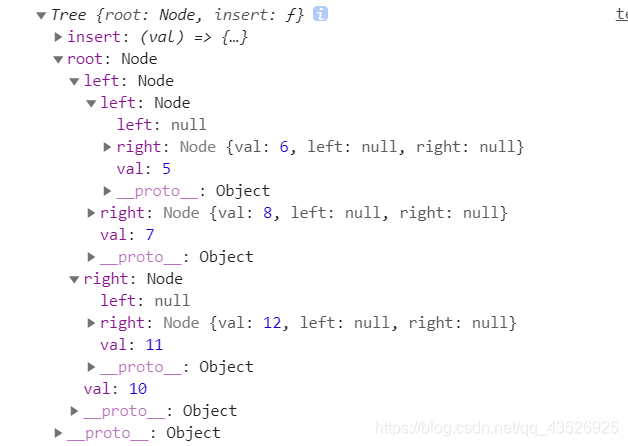
console.log(a);

结果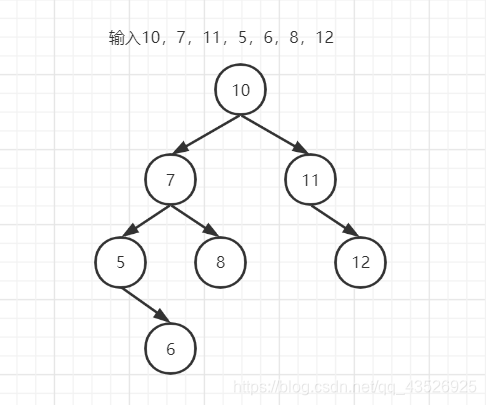：在这里插入图片描述

在这里插入图片描述

二叉树的遍历

深度优先遍历

前序遍历（中左右）
中序遍历（左中右）
后序遍历（左右中）

示例：以实现的二叉树代码进行编写

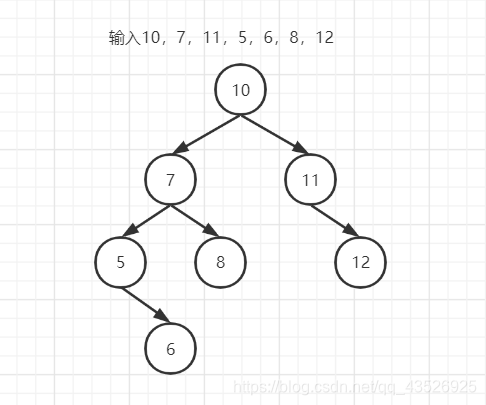
在这里插入图片描述

前序遍历：10，7，5，6，8，11，12（自己心算结果）

this.preErgodic = ()=>{
    //res存储遍历结果
	let res = [];
	function preErgodicTree(root) {
		if(root !== null) {
			res.push(root.val);
			preErgodicTree(root.left);
			preErgodicTree(root.right);
		}
	}
	preErgodicTree(this.root);
	return res;
}
//-----------------输出到控制台
console.log(a.preErgodic());

结果： (7) [10, 7, 5, 6, 8, 11, 12]

图看不到不好算，嘿嘿嘿，放下来好看点

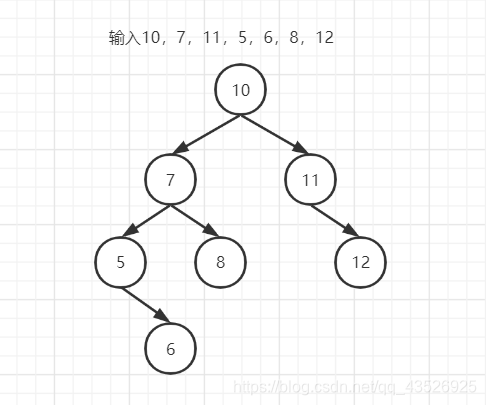
在这里插入图片描述

中序遍历：5，6，7，8，10，11，12（自己心算结果）

this.inOrderErgodic = () => {
    //res存储遍历结果
	let res = [];
	function inOrderErgodicTree(root) {
		if (root !== null) {
			inOrderErgodicTree(root.left);
			res.push(root.val);
			inOrderErgodicTree(root.right);
		}
	}
	inOrderErgodicTree(this.root);
	return res;
}
//-----------------输出到控制台
console.log(a.inOrderErgodic());

结果：(7) [5, 6, 7, 8, 10, 11, 12]

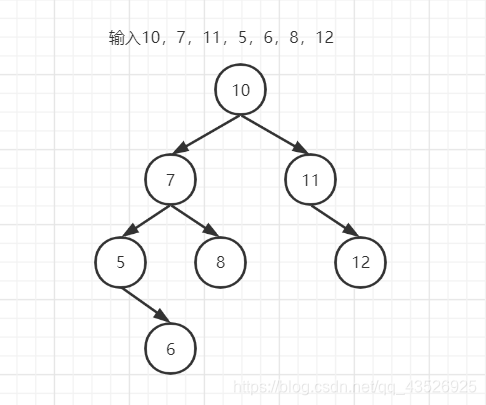
在这里插入图片描述

后序遍历：6，5，8，7，12，11，10

this.postOrderErgodic = () => {
    //res存储遍历结果
	let res = [];
	function postOrderErgodicTree(root) {
		if (root !== null) {
			postOrderErgodicTree(root.left);
			postOrderErgodicTree(root.right);
			res.push(root.val);
		}
	}
	postOrderErgodicTree(this.root);
	return res;
}
//-----------------输出到控制台
console.log(a.postOrderErgodic());

结果：(7) [6, 5, 8, 7, 12, 11, 10]

广度优先遍历

层序遍历

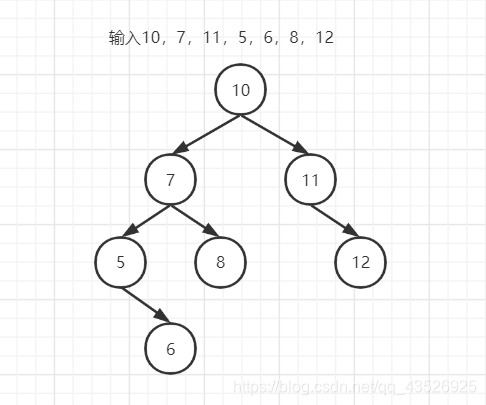
在这里插入图片描述

层序遍历：10，7，11，5，8，12，6

this.sequenceErgodic = () => {
    //存储结果数组
	let res = [];
	//按顺序动态的存入
	let tempArr = [this.root];
	for(let i=0; i<tempArr.length; i++) {
		if(tempArr[i] !== null) {
			res.push(tempArr[i].val);
            //从左到右排列，按顺序压入堆里
			tempArr.push(tempArr[i].left);
			tempArr.push(tempArr[i].right);
		}
	}
    return res;
}
//-----------------输出到控制台
console.log(a.sequenceErgodic());

结果：(7) [10, 7, 11, 5, 8, 12, 6]

树的搜索

还是按照上面的示例接着看

记着二叉搜索树的特点：若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值；若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；它的左、右子树也分别为二叉搜索树。

搜索随机值

this.search = (targetVal) => {
	function searchNode(root, targetVal) {
        //查到最后节点为null返回false
		if(root === null) return false;
        //当需查询值小于当前节点值，即向左子树查找
        //当需查询值大于当前节点值，即向右子树查找
        //相等，即查询到
		if(targetVal < root.val) {
			return searchNode(root.left, targetVal);
		}else if(targetVal > root.val){
			return searchNode(root.right, targetVal);
		}else {
			return true;
		}
	}   
	return searchNode(this.root, targetVal);
}
//-------------------控制台
console.log(a.search(12));

结果：true

查找最大值（最小值雷同）

由于二叉搜索树的性质，找出最大值只需要找到它最右边的节点

//获取最大值
this.searMax = () => {
	//初始结果,保存每一步结果
	let res = null;
	//当前的一个值
	let temp = this.root;
	while(temp !== null) {
		res = temp.val;
		temp = temp.right;
	} 
	return res;
}
//------------------------控制台
console.log(a.searMax());

结果：12

同理，找出最小值即只需要找到它的最左边的节点

this.searMin = () => {
	//初始结果,保存每一步结果
	let res = null;
	//当前的一个值
	let temp = this.root;
	while (temp !== null) {
		res = temp.val;
		temp = temp.left;
	}
	return res;
}
//------------------------控制台
console.log(a.searMin());

结果：5

移除树的节点

移除节点时会出现三种情况

目标节点为叶节点：直接将目标节点更换为null，返回更改的节点
有一个子节点：需要将该子节点补上被移除节点位置上，返回更改的节点
有两个子节点：我这用的示例为二叉搜索树，所以为了保证移除节点后还为二叉搜索树，即需要找到右子节点中的最小值，补充到被移除的节点，再删除以前最小值所在位置节点，返回节点

假设删除数字7
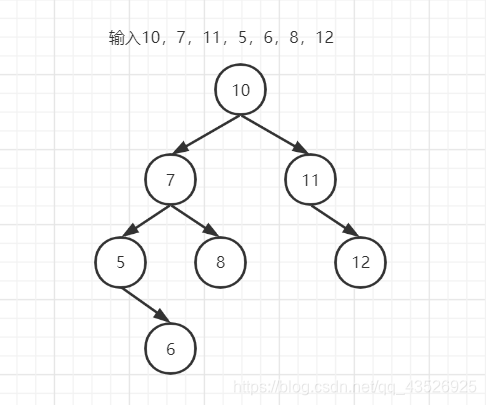
在这里插入图片描述

//移除节点前，需要找到需要移除的节点在树里的什么位置
this.remove = (targetVal) => {
	//防止不输入目标值
	if(!targetVal) return;
	function removeNode(root, targetVal) {
		if(root === null) return null;
		//类似搜索目标值是否存在
		if(targetVal < root.val) {
			//左子树需要修改
			root.left = removeNode(root.left, targetVal);
			return root;
		}else if(targetVal > root.val) {
			//右子树需要修改
			root.right = removeNode(root.right, targetVal);
			return root;
		}else {
			//找到目标结点进行分情况的处理
			//处理叶节点或者一个子节点或者两个子节点时
			if(root.left === null && root.right === null) {
				root = null;
				return root;
			}else if(root.left !== null && root.right === null) {
				root = root.left;
				return root;
			}else if(root.left === null && root.right !== null) {
				root = root.right;
				return root;
			}else{
				//当有两个子节点时候，需要找到右子树的最小值来补到该空缺位置
				//往左子树里找到最小值
				function findMin(root) {
					while(root.left !== null) {
						root = root.left;
					}
					return root.val;
				}
				//最小值
				let temp = findMin(root.right);
				//将最小值补充到被删除位置
				root.val = temp;
				//删除替补值
				root.right = removeNode(root.right, temp);
				//返回节点
				return root;
			}
		}
	}
	//返回移除节点后的树
	this.root = removeNode(this.root, targetVal);
}
//------------------------控制台
a.remove(7);
console.log(a.sequenceErgodic());

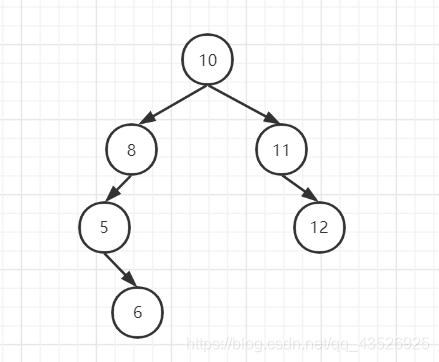
在这里插入图片描述

结果：(6) [10, 8, 11, 5, 12, 6]

完整代码

    <script>
        function Tree() {
            this.root = null;
            this.insert = (val) => {
                let newNode = new Node(val);
                if (this.root === null) {
                    this.root = newNode;
                } else {
                    insertNode(this.root, newNode);
                }
            }
            //每一棵树都有他的节点方法
            function Node(val) {
                this.val = val;
                this.left = null;
                this.right = null;
            }
            //插入方法
            function insertNode(node, newNode) {
                if (node.val > newNode.val) {
                    if (node.left === null) {
                        node.left = newNode;
                    } else {
                        insertNode(node.left, newNode);
                    }
                } else {
                    if (node.right === null) {
                        node.right = newNode;
                    } else {
                        insertNode(node.right, newNode);
                    }
                }
            }
            //前序遍历
            this.preErgodic = () => {
                let res = [];
                function preErgodicTree(root) {
                    if (root !== null) {
                        res.push(root.val);
                        preErgodicTree(root.left);
                        preErgodicTree(root.right);
                    }
                }
                preErgodicTree(this.root);
                return res;
            }
            //中序遍历
            this.inOrderErgodic = () => {
                let res = [];
                function inOrderErgodicTree(root) {
                    if (root !== null) {
                        inOrderErgodicTree(root.left);
                        res.push(root.val);
                        inOrderErgodicTree(root.right);
                    }
                }
                inOrderErgodicTree(this.root);
                return res;
            }
            //后序遍历
            this.postOrderErgodic = () => {
                let res = [];
                function postOrderErgodicTree(root) {
                    if (root !== null) {
                        postOrderErgodicTree(root.left);
                        postOrderErgodicTree(root.right);
                        res.push(root.val);
                    }
                }
                postOrderErgodicTree(this.root);
                return res;
            }
            //层序遍历
            this.sequenceErgodic = () => {
                let res = [];
                //临时存储
                let tempArr = [this.root]; //当前
                for (let i = 0; i < tempArr.length; i++) {
                    if (tempArr[i] !== null) {
                        res.push(tempArr[i].val);
                        tempArr.push(tempArr[i].left);
                        tempArr.push(tempArr[i].right);
                    }
                }
                return res;
            }
            //搜索目标值是否存在
            this.search = (targetVal) => {
                function searchNode(root, targetVal) {
                    if (root === null) return false;
                    if (targetVal < root.val) {
                        return searchNode(root.left, targetVal);
                    } else if (targetVal > root.val) {
                        return searchNode(root.right, targetVal);
                    } else {
                        return true;
                    }
                }
                return searchNode(this.root, targetVal);
            }
            //获取最大值
            this.searMax = () => {
                //初始结果,保存每一步结果
                let res = null;
                //当前的一个值
                let temp = this.root;
                while (temp !== null) {
                    res = temp.val;
                    temp = temp.right;
                }
                return res;
            }
            //获取最小值
            this.searMin = () => {
                //初始结果,保存每一步结果
                let res = null;
                //当前的一个值
                let temp = this.root;
                while (temp !== null) {
                    res = temp.val;
                    temp = temp.left;
                }
                return res;
            }
            //移除节点
            //移除节点前，需要找到需要移除的节点在树里的什么位置
            this.remove = (targetVal) => {
                //防止不输入目标值
                if(!targetVal) return;
                function removeNode(root, targetVal) {
                    if(root === null) return null;
                    //类似搜索目标值是否存在
                    if(targetVal < root.val) {
                        //左子树需要修改
                        root.left = removeNode(root.left, targetVal);
                        return root;
                    }else if(targetVal > root.val) {
                        //右子树需要修改
                        root.right = removeNode(root.right, targetVal);
                        return root;
                    }else {
                        //找到目标结点进行分情况的处理
                        //处理叶节点或者一个子节点或者两个子节点时
                        if(root.left === null && root.right === null) {
                            root = null;
                            return root;
                        }else if(root.left !== null && root.right === null) {
                            root = root.left;
                            return root;
                        }else if(root.left === null && root.right !== null) {
                            root = root.right;
                            return root;
                        }else{
                            //当有两个子节点时候，需要找到右子树的最小值来补到该空缺位置
                            //往左子树里找到最小值
                            function findMin(root) {
                                while(root.left !== null) {
                                    root = root.left;
                                }
                                return root.val;
                            }
                            //最小值
                            let temp = findMin(root.right);
                            //将最小值补充到被删除位置
                            root.val = temp;
                            //删除替补值
                            root.right = removeNode(root.right, temp);
                            //返回节点
                            return root;
                        }

                    }
                }
                //返回移除节点后的树
                this.root = removeNode(this.root, targetVal);
            }
        }
        let a = new Tree();
        a.insert(10);
        a.insert(7);
        a.insert(11);
        a.insert(5);
        a.insert(6);
        a.insert(8);
        a.insert(12);
        a.remove(7);
    </script>

                 //删除替补值
                        root.right = removeNode(root.right, temp);
                        //返回节点
                        return root;
                    }

                }
            }
            //返回移除节点后的树
            this.root = removeNode(this.root, targetVal);
        }
    }
    let a = new Tree();
    a.insert(10);
    a.insert(7);
    a.insert(11);
    a.insert(5);
    a.insert(6);
    a.insert(8);
    a.insert(12);
    a.remove(7);
</script>