1.树的存储结构
(1)双亲表示法
? ?一组连续空间存储树的结点,同时在每个结点中,附设一个指示器指示其双亲结点在数组中的位置。
结点结构:
typedef struct PTNode {
int data;//数据域,存储结点的数据信息
int parent;//位置域,存储该结点的双亲在数组中的下标
}PTNode;? 双亲表示法是使用数组来表示的。
树结构:
typedef struct {
PTNode node[MaxSize];//结点数组
int r, n;//r表示根的位置,n表示结点数
}PTree;由于根结点是没有双亲的,所以我们约定根结点的位置域设置为-1。结点自己的位置用下标表示。
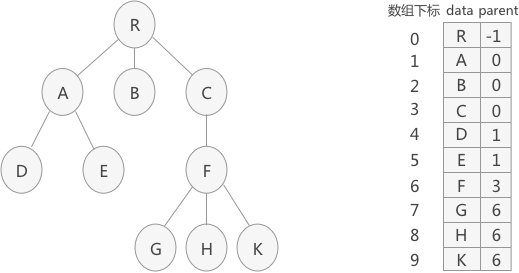
(2)孩子表示法
? ? ? ?把每个结点的孩子排列起来,以单链表作存储结构,则n个结点有n个孩子链表。如果是叶子结点则此单链表为空。然后n个头指针又组成了一个线性表,采取顺序存储结构,存放进一个一维数组中。
孩子链表的孩子结点:
typedef struct CTNode {
int child;//数据域,存储某个结点在表头数组中的下标
struct CTNode* next;//指针域,存储指向表头结点的下一个孩子结点的指针
}*ChildPtr;?表头数组的表头结点:
typedef struct {
int data;//数据域,存储表头结点的数据信息
ChildPtr firstchild;//头指针域,存储表头结点的孩子链表的头指针(指向第一个孩子)
}CTBox;树结构:
typedef struct {
CTBox nodes[MaxSize];//结点数组
int r, n;//r表示根的位置,n表示结点数
}CTree;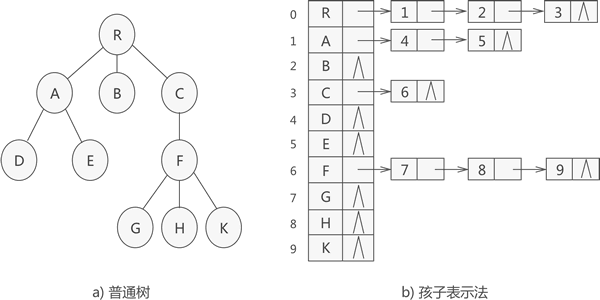
?(3)孩子兄弟表示法
? 任意一棵树,它的结点的第一个孩子如果存在就是唯一的,它的右兄弟如果存在也是唯一的。因此,我们设置两个指针,分别指向该结点的第一个孩子和此孩子的右兄弟。
typedef struct CSNode {
int data;
struct CSNode* firstchild, * rightsib;
}CSNode,*CSTree;? data是数据域,firstchild为指针域,存储该结点的第一个孩子结点的存储地址,rightsib是指针域,存储该结点的右兄弟结点的存储地址。(类似二叉链表)
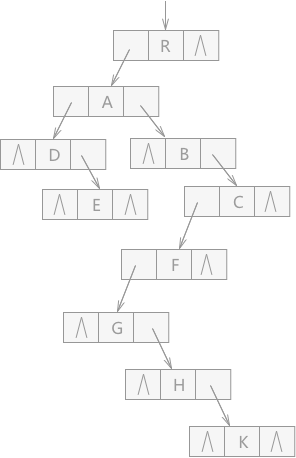
?2.二叉树
(1)二叉树的链式存储结构
? ?二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域。我们称这样的链表为二叉链表。
typedef struct BiTNode {
int data;
struct BiTNode* lchild, * rchild;//左右孩子指针
}BiTNode,*BiTree;?二叉树的顺序存储结构就是声明一个数组,然后把二叉树按照层次遍历的顺序(从上到下,从左到)标上序号,按照序号存储到数组中即可。
?(2)遍历二叉树
? ? 1.前序遍历
int PreOrderTraverse(BiTree T) {
if (T == NULL)
return 1;
else {
printf("%c ", T->data);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
}? 规则是若二叉树为空,则空操作返回,否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。
? ? 2.中序遍历
int InOrderTraverse(BiTree T) {
if (T == NULL)
return 1;
else {
InOrderTraverse(T->lchild);
printf("%c ", T->data);
InOrderTraverse(T->rchild);
}
}? 规则是若树为空,则空操作返回,否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。、
? ? 3.后序遍历
int PostOrderTraverse(BiTree T) {
if (T == NULL)
return 1;
else {
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
printf("%c ", T->data);
}
}?规则是若树为空,则空操作返回,否则先后序遍历左子树,再后序遍历右子树,最后访问根结点。
? ?4.层序遍历
int LevelOrderTraverse(BiTree& t) {
queue<BiTNode*> q;//声明一个数据类型为结点指针的队列q
BiTNode* h;//声明一个结点指针
if (t != NULL) {
q.push(t);//把结点指针入队
while (!q.empty()) {
h = q.front();//取出首位元素
q.pop();//首位元素出队
printf("%c ", h->data);
if (h->lchild != NULL) {
q.push(h->lchild);//入队左孩子
}
if (h->rchild != NULL) {
q.push(h->rchild);//入队右孩子
}
}
}
return 1;
}? ?规则是若树为空,则空操作返回。否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
(3)建立二叉树
?这里选择先序序列(前序序列)来建立二叉树
int CreateBiTree(BiTree& T) {
char ch;
cin >> ch;
if (ch == '#')
T = NULL;//如果输入的字符为'#',说明这是个空结点
else {
T = new BiTNode;
if (!T)
return OVERFLOW;
T->data = ch;
CreateBiTree(T->lchild);//建立左子树
CreateBiTree(T->rchild);//建立右子树
}
return 1;
}
? 按照先序遍历的顺序输入各个结点的内容。这里值得注意的地方——要把空结点也输入进去,用'#'符号代表空结点。否则二叉树的建立将永远持续下去。举例:下图对应的输入操作应该是? A B D # # E # # C F # # #
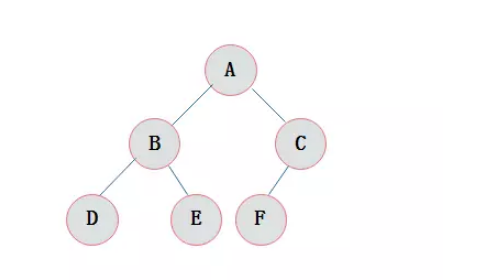
示例:
int main()
{
BiTree t=NULL;
cout << "请构造一棵树:";
CreateBiTree(t);
cout << "先序遍历的结果是:";
PreOrderTraverse(t);
cout << endl;
cout << "中序遍历的结果是:";
InOrderTraverse(t);
cout << endl;
cout << "后序遍历的结果是:";
PostOrderTraverse(t);
cout << endl;
cout << "层次遍历的结果是:";
LevelOrderTraverse(t);
return 0;
}
(4)计算二叉树深度
int Depth(BiTree T) {
if (T == NULL)
return 0;
else {
int m = Depth(T->lchild);//左子树的深度
int n = Depth(T->rchild);//右子树的深度
if (m > n)//如果左子树深度较大
return m + 1;//返回左子树深度+1(带上根结点那层)
else
return n + 1;//否则返回右子树深度+1
}
}?若是空树,深度为0。否则递归计算左子树的深度为m,递归计算右子树的深度为n,二叉树的深度则为m与n的较大者+1。
(5)计算二叉树结点总数
int NodeCount(BiTree T) {
if (T == NULL)
return 0;//为空的结点不能算作结点
else
return NodeCount(T->lchild) + NodeCount(T->rchild) + 1;
}?若是空树,则结点为0(并且递归到空结点的时候也不能算作结点)。如果不是空树,则结点个数为左子树的结点+右子树的结点+1(根)。
(6)计算二叉树叶子结点总数
int LeafCount(BiTree T) {
if (T == NULL)
return 0;//空树返回0
if (T->lchild == NULL && T->rchild == NULL)//叶子结点的判断条件——没有孩子
return 1;//叶子结点返回1
else
return LeafCount(T->lchild) + LeafCount(T->rchild);//根的左子树叶子结点和右子树叶子结点的和
}? 如果树为空则为0。如果是叶子结点返回1。二叉树叶子结点总数为根的左子树叶子结点个数+右子树叶子结点个数。
示例:
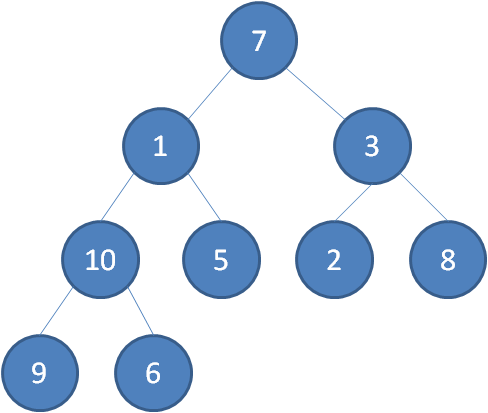
?7 1 10 9 # # 6 # # 5 # # 3 2 # # 8 # #?
?注意这里的10,由于输入的相当于字符型,所以会被拆成1和0分别输入进去,因此要换一种表示方法——输入整形,用-1表示空结点。
?7 1 10 9 -1 -1 6 -1 -1 6 -1 -1 3 2 -1 -1 8 -1 -1
int main()
{
BiTree t=NULL;
cout << "请构造一棵树:";
CreateBiTree(t);
cout << "二叉树的深度为:";
printf("%d", Depth(t));
cout << endl;
cout << "二叉树的结点总数为:";
printf("%d", NodeCount(t));
cout << endl;
cout << "二叉树的叶子结点总数为:";
printf("%d", LeafCount(t));
cout << endl;
return 0;
}
?