线性表及其实现
1 多项式的表示
1.1 方法一:顺序存储结构直接表示

1.2 顺序存储结构表示非零项
用结构数组表示:数组分量是由系数
a
i
a_i
ai?、指数
i
i
i组成的结构,对应一个非零项。
(
a
i
,
i
)
(a_i,i)
(ai?,i)
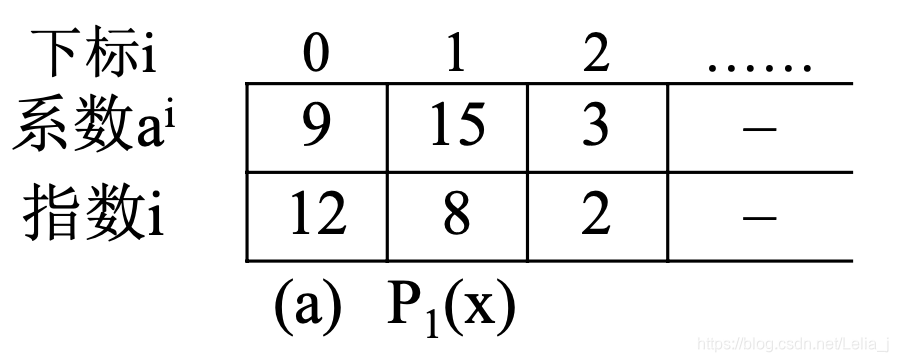
按指数大小有序存储
1.3 链表结构存储非零项

2 线性表及其实现
线性表:由同类型数据元素构成有序序列的线性结构
2.1 线性表的抽象数据类型描述

2.1.1 顺序存储实现
利用数组的连续存储空间顺序存放线性表的各元素
2.1.2 链式存储实现
不要求逻辑上相邻的两个元素物理上也相邻;通过“链”建立起数据元素之间的逻辑关系。
? 插入、删除不需要移动数据元素,只需要修改“链”。
2.2 广义表
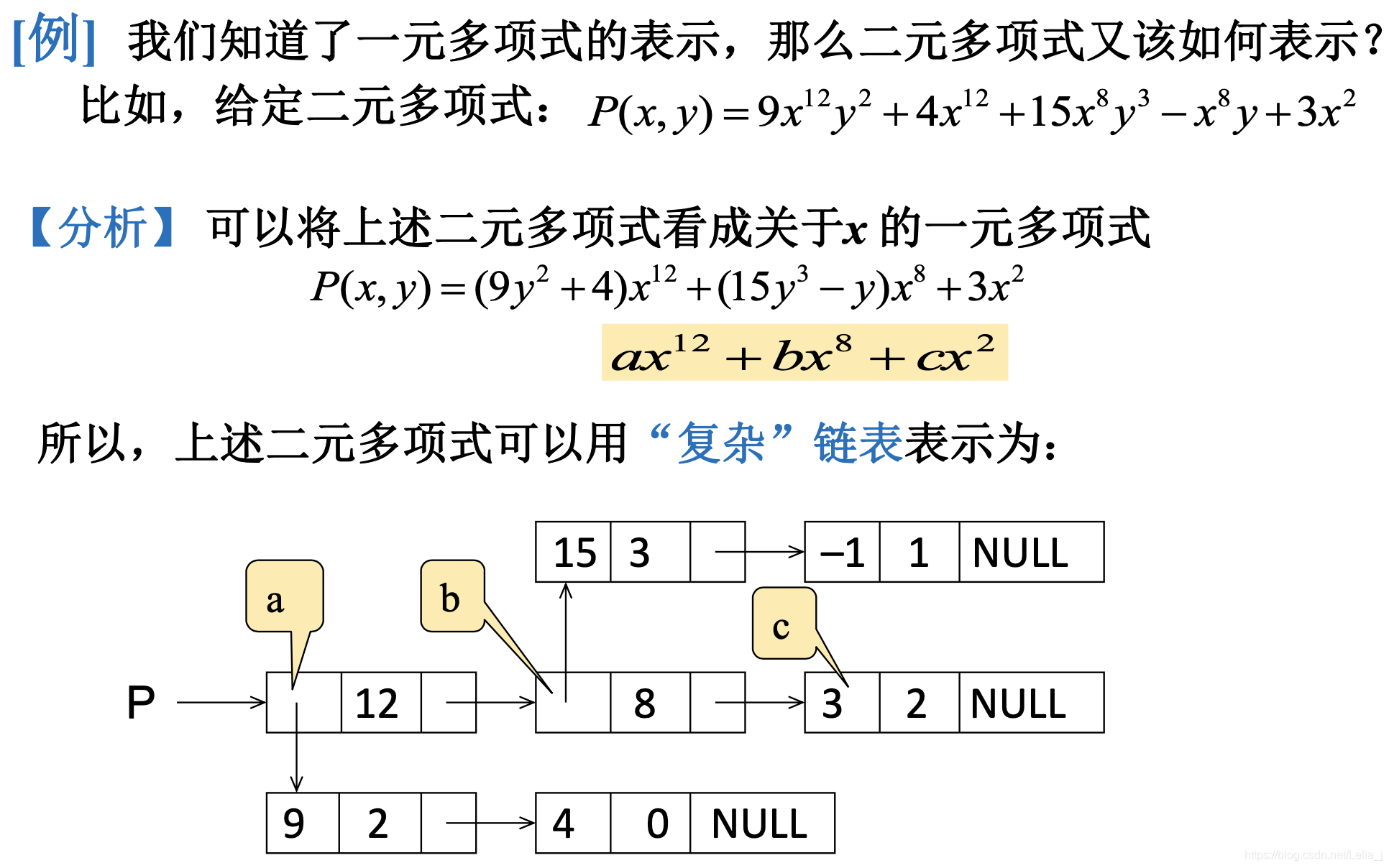
广义表中,元素不仅可以是单元素也可以是另一个广义表。
2.3 多重链表
链表中的节点可能同时隶属于多个链
- 多重链表中节点的指针域会有多个;
- 但包含两个指针域的链表并不一定是多重链表,例如双向链表。
- 应用:树、图
例:
稀疏矩阵:非零项很少的矩阵,造成空间浪费。
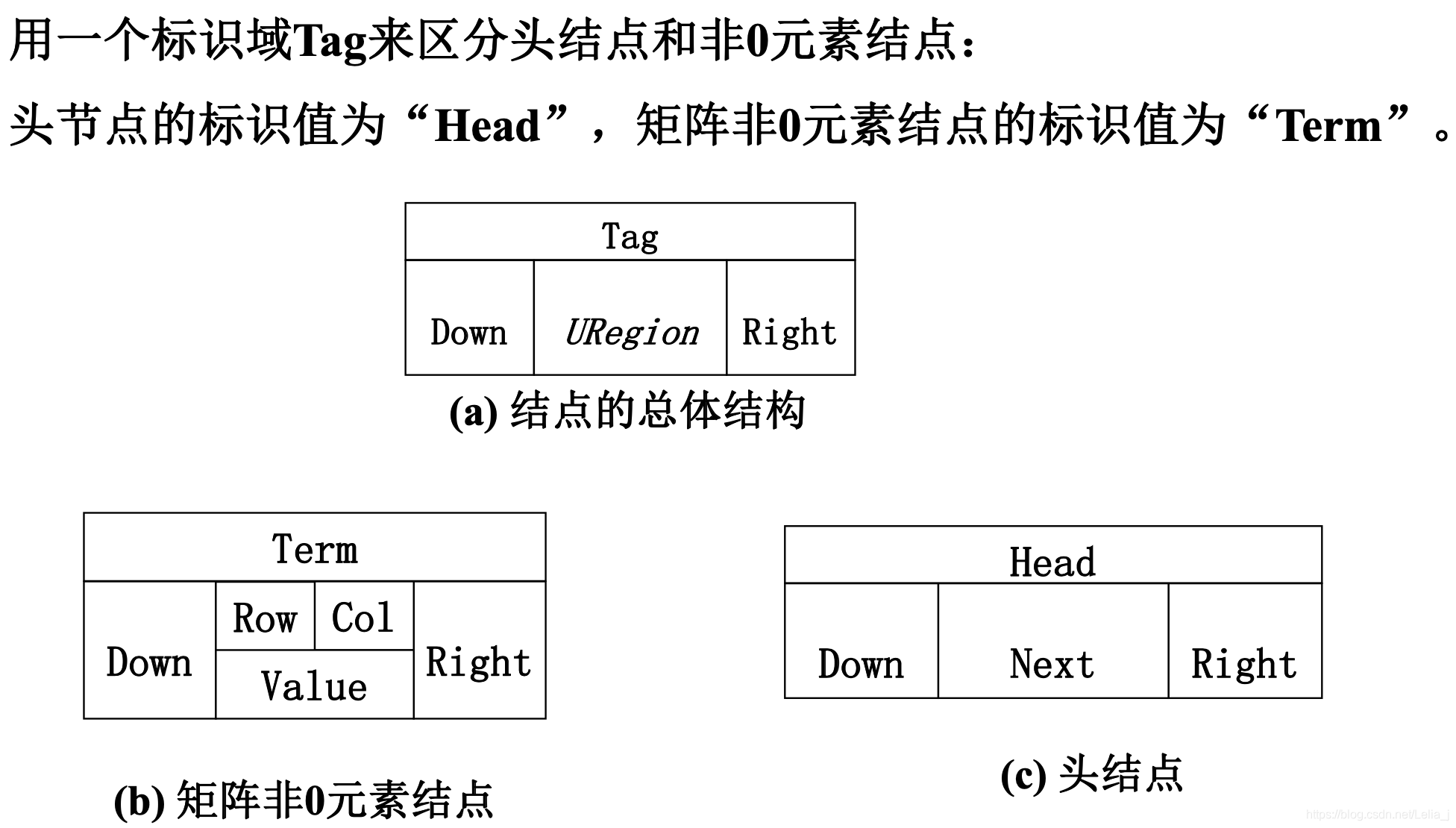
采用一种典型多重链表——十字链表来存储稀疏矩阵
- 只存储矩阵非0元素项
结点的数据域:行坐标Row、列坐标Col、数值Value - 每个结点通过两个指针域,把同行、同列串起来;
– 行指针(或称为向右指针)Right
– 列指针(或称为向下指针)Down
3 堆栈
3.1 堆栈的抽象数据类型描述
堆栈(Stack):具有一定操作约束的线性表
只在一端(栈顶,Top)做插入、删除
- 插入数据:入栈(Push)
- 删除数据:出栈(Pop)
- 后入先出:Last In First Out(LIFO)

3.1.1 顺序存储实现
栈的顺序存储结构通常由一个一维数组和一个记录栈顶元素位置的变量组成。
例:请用一个数组实现两个堆栈,要求最大地利用数组空间,使数组只要有空间入栈操作就可以成功。
答:一种比较聪明的方法是使这两个栈分别从数组的两头开始向中间生长;当两个栈的栈顶指针相遇时,表示两个栈都满了。
#define MaxSize <存储数据元素的最大个数>
struct DStack {
ElementType Data[MaxSize];
int Top1; /* 堆栈1的栈顶指针 */
int Top2; /* 堆栈2的栈顶指针 */
} S;
S.Top1 = -1;
S.Top2 = MaxSize;
3.1.2 链式存储实现
栈的链式存储结构实际上就是一个单链表,叫做链栈。插入和删除操作只能在链栈的栈顶进行。
栈顶指针Top应该在链表的链头
3.2 堆栈的应用
3.2.1 表达式的求值
后缀表达式求值
中缀表达式求值:转为后缀表达式
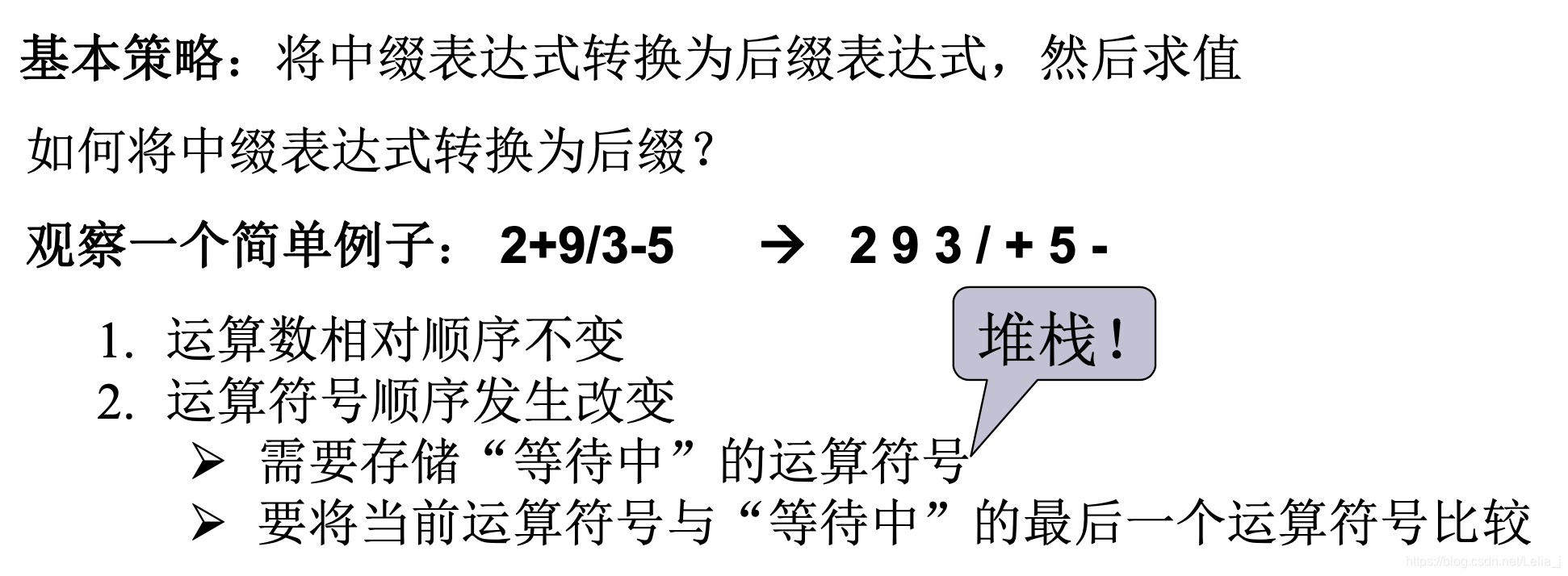
转换方式:

例:

3.2.2 其他应用
- 函数调用及递归实现
- 深度优先搜索
- 回溯算法
4 队列
4.1 队列的抽象数据类型描述
队列(Queue):具有一定操作约束的线性表
插入和删除操作:只能在一端插入,而在另一端删除。
- 数据插入:入队列(AddQ)
- 数据删除:出队列(DeleteQ)
- 先来先服务
- 先进先出:FIFO

4.1.1 顺序存储实现
队列的顺序存储结构通常由一个一维数组和一个记录队列头元素位置的变量front以及一个记录队列尾元素位置的变量rear组成。
循环队列:
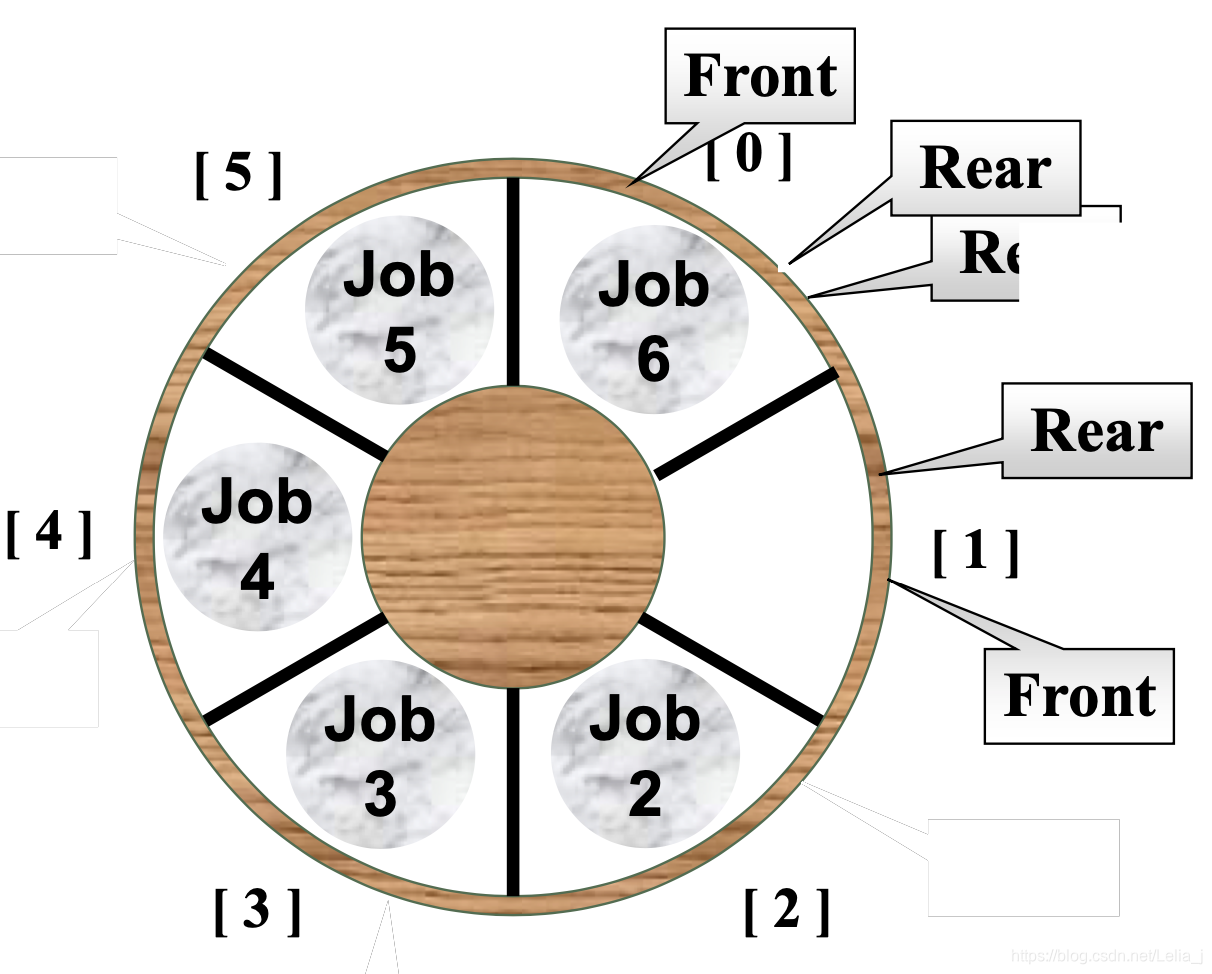
队列空和满的判别条件:
使用额外标记:Size或Tag域;或者仅使用n-1个数组空间
4.1.2 链式存储实现
队列的链式存储结构也可以用一个单链表实现。
插入和删除操作分别在链表的两头进行。
front在链表头,rear在链表尾,因为尾部不好做删除
题外话:学习好困好困,坚持住!