前言:
大家好,上一篇博客带大家学习如何编写十大排序算法中的三大简单排序,那么今天带给大家的学习内容是十大排序算法中的希尔排序算法
1.1 希尔排序基础概念
在编写希尔排序算法之前,我们首先简单了解一下希尔排序的基本概念和排序的流程,会对算法的编写很有帮助!
1.1.1 希尔排序基本概念
-
希尔排序又称改进版插入排序;它是按照一定的间隔将查找到的元素进行排序,相比插入排序,将小数排在前面,所移动的次数要少很多
-
当间隔较大时,它移动的次数比较少,当间隔较小 (例如为1时),移动的距离又比较小,所以希尔排序要比普通的插入排序效率高,但由于它是跳着排序,所以不稳定
1.1.2 希尔排序执行流程
- 间隔为4 第一轮排序
从数组中下标0位置开始,首先按照每隔4位(从当前下标下一位开始计算)选出一位数,然后将这些间隔为4的数进行排序
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 9 | 6 | 11 | 3 | 5 | 12 | 8 | 7 | 10 | 15 | 14 | 4 | 1 | 13 | 2 |
| 1 | 6 | 11 | 3 | 5 | 12 | 8 | 7 | 9 | 15 | 14 | 4 | 10 | 13 | 2 |
- 间隔为4 第二轮排序
从数组下标1位置开始,重复上述操作
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 11 | 3 | 5 | 12 | 8 | 7 | 9 | 15 | 14 | 4 | 10 | 13 | 2 |
| 1 | 6 | 11 | 3 | 5 | 12 | 8 | 7 | 9 | 13 | 14 | 4 | 10 | 15 | 2 |
- 间隔为4 第三轮排序
从数组下标2位置开始,重复上述步骤
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 11 | 3 | 5 | 12 | 8 | 7 | 9 | 13 | 14 | 4 | 10 | 15 | 2 |
| 1 | 6 | 2 | 3 | 5 | 12 | 8 | 7 | 9 | 13 | 11 | 4 | 10 | 15 | 14 |
- 间隔为4 最终排序结果
从数组下标3位置开始,重复上述步骤
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 2 | 3 | 5 | 12 | 8 | 7 | 9 | 13 | 11 | 4 | 10 | 15 | 14 |
| 1 | 6 | 2 | 3 | 5 | 12 | 8 | 4 | 9 | 13 | 11 | 7 | 10 | 15 | 14 |
缩小间隔为2继续进行新一轮的排序,再将间隔分别调整为2继续进行排序,直到最后间隔为1排序完结束
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 2 | 3 | 5 | 12 | 8 | 4 | 9 | 13 | 11 | 7 | 10 | 15 | 14 |
| 1 | 6 | 2 | 3 | 5 | 12 | 8 | 4 | 9 | 13 | 11 | 7 | 10 | 15 | 14 |
- 间隔为2 排序结果
间隔为2的红色数字先排序,然后间隔为2的橙色数字再排序
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 6 | 2 | 3 | 5 | 12 | 8 | 4 | 9 | 13 | 11 | 7 | 10 | 15 | 14 |
| 1 | 6 | 2 | 3 | 5 | 12 | 8 | 4 | 9 | 13 | 10 | 7 | 11 | 15 | 14 |
| 1 | 3 | 2 | 4 | 5 | 6 | 8 | 7 | 9 | 12 | 10 | 13 | 11 | 15 | 14 |
- 间隔为1 排序结果
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 2 | 4 | 5 | 6 | 8 | 7 | 9 | 12 | 10 | 13 | 11 | 15 | 14 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
1.2 希尔排序算法实现
1.2.1 希尔排序代码实现
1.初次编写希尔排序
由于希尔排序是插入排序的改进版,如果编写时没有思路,可以先写一个插入排序,然后在其基础上慢慢修改
- 代码实现
package com.kuang.review2;
/**
* @ClassName ShellSort
* @Description 希尔排序算法
* @Author 狂奔の蜗牛rz
* @Date 2021/8/17
*/
public class ShellSort {
public static void main(String[] args) {
//初始化待排序数组
int[] arr = {9,6,11,3,5,12,8,7,10,15,14,4,1,13,2};
//调用核心排序算法
sort1(arr);
//最终排序结果
System.out.println("最终排序结果为:");
//打印排序接货
print(arr);
}
/**
* 插入排序算法
* @param arr 待排序整型元素
*/
static void sort1(int[] arr) {
//外层for循环
for (int i = 1; i < arr.length; i++) {
//内层for循环
for (int j = i; j > 0; j--) {
//判断当前下标的元素值是否小于上一个下标元素
if(arr[j] < arr[j-1]) {
//若当前元素值小于上一个元素, 则交换两者的值
swap(arr, j,j-1);
}
}
//打印每轮排序结果
System.out.println("第"+i+"轮排序结果为:");
//打印排序结果
print(arr);
}
}
/**
* 交换两个元素值
* @param arr 待排序整型数组
* @param i 元素1下标
* @param j 元素2下标
*/
static void swap(int[] arr, int i, int j) {
//首先将i下标元素值赋给temp(临时变量)
int temp = arr[i];
//然后将j下标元素值赋给i下标元素
arr[i] = arr[j];
//最后将temp(临时变量)值赋给j下标元素
arr[j] = temp;
}
/**
* 打印排序结果
* @param arr 待排序整型数组
*/
static void print(int[] arr) {
//for循环遍历数组元素
for (int i = 0; i < arr.length; i++) {
//打印排序后结果
System.out.println(arr[i]+" ");
}
}
}
- 测试结果
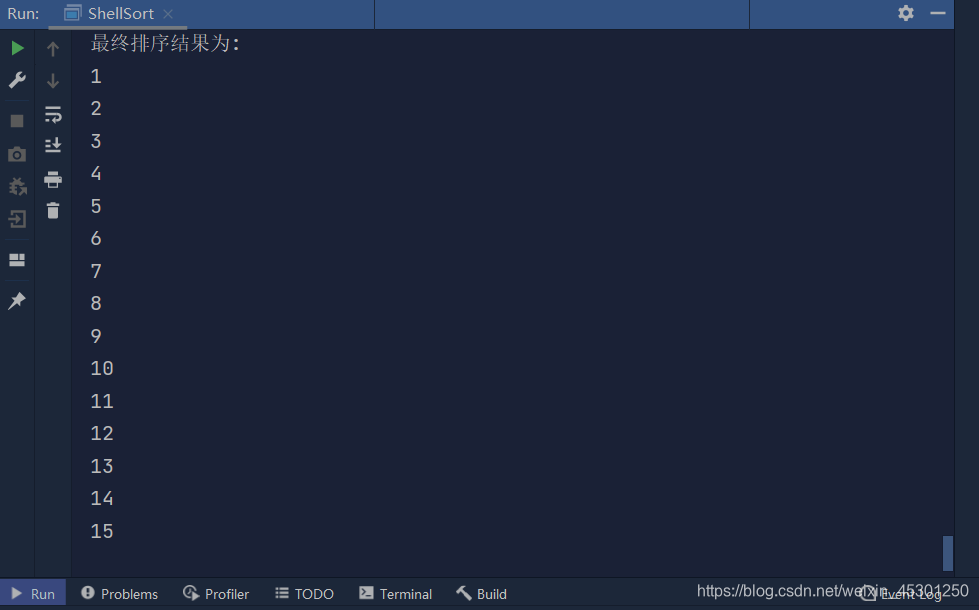
结果:元素从小到大排列,排序结果正确!
2.希尔排序算法改进1
在插入排序算法基础上,引入排序的间隔,将其修改为希尔排序
- 代码实现
package com.kuang.review2;
/**
* @ClassName ShellSort
* @Description 希尔排序算法
* @Author 狂奔の蜗牛rz
* @Date 2021/8/17
*/
public class ShellSort {
public static void main(String[] args) {
//初始化待排序数组
int[] arr = {9,6,11,3,5,12,8,7,10,15,14,4,1,13,2};
//调用核心排序算法
/**
* 由于此时gap值还不能动态变化, 因此最终的排序结果是gap间隔为4的排序结果,
* 测试结果为:1 6 2 3 5 12 8 4 9 13 11 7 10 15 14, 与上面的预测结果一致
*/
sort2(arr);
//最终排序结果
System.out.println("最终排序结果为:");
//打印排序接货
print(arr);
}
/**
* 希尔排序算法 第一版
* 在插入排序基础上使用间隔排序, 但间隔不能动态变化
* @param arr 待排序整型元素
*/
static void sort2(int[] arr) {
//插入排序外层for循环
// for (int i = 1; i < arr.length; i++) {
/**
* 希尔排序按照间隔跳着排序, 先设置一个gap间隔,
* 其初值为4, 表示初始间隔为4
*/
int gap = 4;
/**
* 将外层循环中的i初值修改为gap, i的范围为小于数组的长度
* 问题思考: 自增是i++还是i+gap?
* 由于间隔之间的前后元素还要进行比较, 所以是i++
*/
for (int i = gap; i < arr.length; i++) {
//插入排序的内层for循环
// for (int j = i; j > 0; j--) {
/**
* 希尔排序的内层循环j的初值仍为i吗?
* 由于内层循环是从下标为gap值位置开始进行遍历的, 所以j的初值为gap,
* 而外层循环中i的初值设置为gap, 因此j的初值为i
*
* j的范围还是大于0?
* 由于外层循环结束后, 每轮的gap间隔值要发生变化, 从4到3,再到2, 直到最后变为1,
* 所以gap和j的差值应该小于1, 即 gap - j < 1, 再优化一下就变成了: j > gap - 1
*
* 自增是j--还是j-=gap?
* 由于当前元素要与前面间隔值为gap大小的元素进行比较, 所以自增为j-=gap
*/
//希尔排序的内层循环
for (int j = i; j > gap-1 ; j-=gap) {
//判断当前下标的元素值是否小于上一个下标元素
// if(arr[j] < arr[j-1]) {
/**
* 由于内层循环的自增为j-=gap, 所以j的上一个元素下标为j-gap
*/
if(arr[j] < arr[j-gap]) {
//若当前元素值小于上一个元素, 则交换两者的值
// swap(arr, j,j-1);
/**
* 交换前后值大小的上一个元素下标修改为j-gap
*/
swap(arr, j,j-gap);
}
}
//打印每轮排序结果
System.out.println("第"+i+"轮排序结果为:");
//打印排序结果
print(arr);
}
}
/**
* 交换两个元素值
* @param arr 待排序整型数组
* @param i 元素1下标
* @param j 元素2下标
*/
static void swap(int[] arr, int i, int j) {
//首先将i下标元素值赋给temp(临时变量)
int temp = arr[i];
//然后将j下标元素值赋给i下标元素
arr[i] = arr[j];
//最后将temp(临时变量)值赋给j下标元素
arr[j] = temp;
}
/**
* 打印排序结果
* @param arr 待排序整型数组
*/
static void print(int[] arr) {
//for循环遍历数组元素
for (int i = 0; i < arr.length; i++) {
//打印排序后结果
System.out.println(arr[i]+" ");
}
}
}
- 测试结果
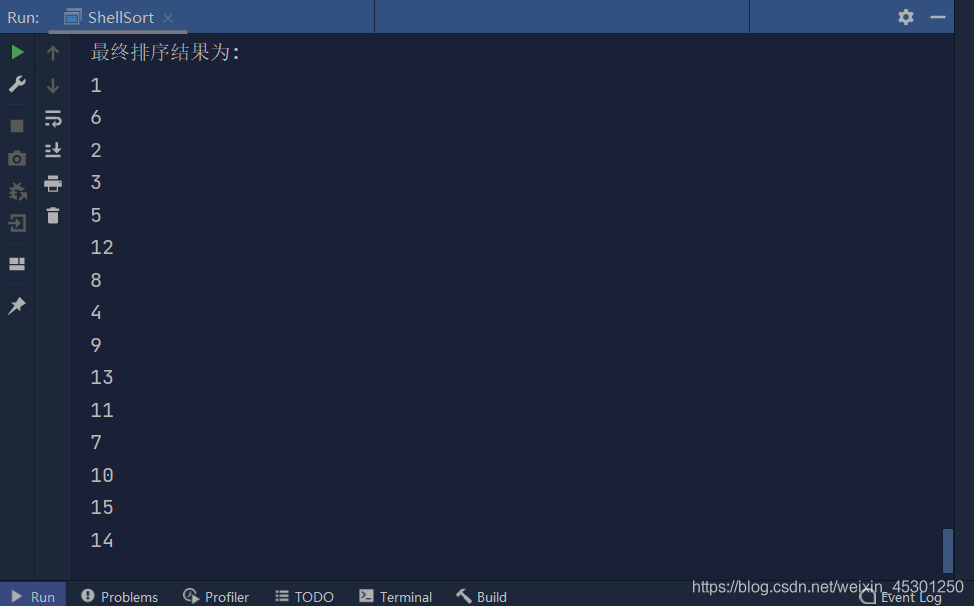
结果:与间隔为4的排序结果相同!
3.希尔排序算法改进2
在希尔排序算法第一版基础上,将排序间隔修改为动态变化
- 编写代码
package com.kuang.review2;
/**
* @ClassName ShellSort
* @Description 希尔排序算法
* @Author 狂奔の蜗牛rz
* @Date 2021/8/17
*/
public class ShellSort {
public static void main(String[] args) {
//初始化待排序数组
int[] arr = {9,6,11,3,5,12,8,7,10,15,14,4,1,13,2};
//调用核心排序算法
sort3(arr);
//最终排序结果
System.out.println("最终排序结果为:");
//打印排序接货
print(arr);
}
/**
* 希尔排序算法 改进第二版
* 在改进第一版基础上, gap间隔值能够进行动态变化
* @param arr 待排序整型元素
*/
static void sort3(int[] arr) {
//gap间隔的初值为4
// int gap = 4;
//定义一个num变量, 用来记录排序次数
int num = 0;
/**
* 由于gap间隔值需要动态变化, 所以需要在外循环外再加一层循环
* gap的初值仍为4开始, gap的范围大于0即可;
* 第一个外层for循环的自增怎样设置?
* 假设从4到2, 最终变为1为止, 也就是gap值对半取, 即gap/=2
*/
//第一个外层循环
// for (int gap = 4; gap > 0; gap/=2) {
/**
* 将最外层循环中的gap间隔值改为每次都对数组长度取半, 处理效率会比gap的初值为4高
*/
for (int gap = arr.length/2; gap > 0; gap/=2) {
//第二个外层循环
for (int i = gap; i < arr.length; i++) {
//希尔排序的内层循环
for (int j = i; j > gap-1 ; j-=gap) {
//判断当前下标的元素值是否小于上一个下标元素
if(arr[j] < arr[j-gap]) {
//若当前元素值小于上一个元素, 则交换两者的值
swap(arr, j,j-gap);
}
}
}
//每轮外层循环结束后, num计数器加1
num++;
//每轮排序结果
System.out.println("间隔为"+gap+"时, 第"+ num +"轮排序结果为:");
//打印排序结果
print(arr);
}
}
/**
* 交换两个元素值
* @param arr 待排序整型数组
* @param i 元素1下标
* @param j 元素2下标
*/
static void swap(int[] arr, int i, int j) {
//首先将i下标元素值赋给temp(临时变量)
int temp = arr[i];
//然后将j下标元素值赋给i下标元素
arr[i] = arr[j];
//最后将temp(临时变量)值赋给j下标元素
arr[j] = temp;
}
/**
* 打印排序结果
* @param arr 待排序整型数组
*/
static void print(int[] arr) {
//for循环遍历数组元素
for (int i = 0; i < arr.length; i++) {
//打印排序后结果
System.out.println(arr[i]+" ");
}
}
}
- 测试结果
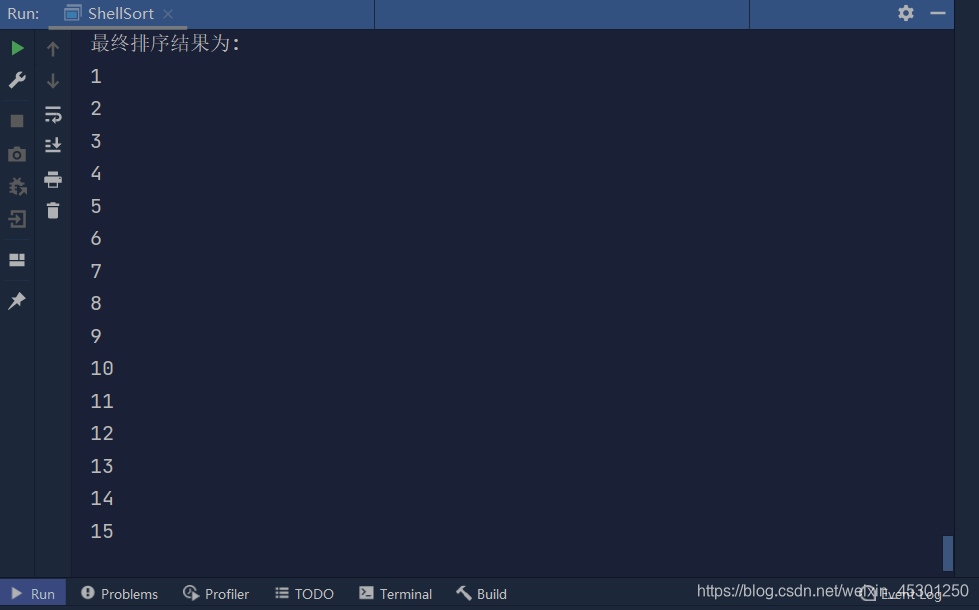
结果:元素从小到大排序,排序结果正确!
4. 希尔排序算法改进3
在希尔排序改进第二版基础上,使用Knuth序列进行优化
- 代码实现
package com.kuang.review2;
/**
* @ClassName ShellSort
* @Description 希尔排序算法
* @Author 狂奔の蜗牛rz
* @Date 2021/8/17
*/
public class ShellSort {
public static void main(String[] args) {
//初始化待排序数组
int[] arr = {9,6,11,3,5,12,8,7,10,15,14,4,1,13,2};
//调用核心排序算法
sort4(arr);
//最终排序结果
System.out.println("最终排序结果为:");
//打印排序接货
print(arr);
}
/**
* 希尔排序算法 改进第三版
* 在改进第二版基础上, 使用Knuth序列进行优化
* @param arr 待排序整型元素
*/
static void sort4(int[] arr) {
/**
* 什么是Knuth序列?
* 即满足公式 h=1, ... , h = 3*h + 1;
* 代入公式可以得到: 1, 3*1+1=4, 3*4+1=13,...
*/
//定义一个num变量, 用来记录排序次数
int num = 0;
/**
* 使用Knuth序列(h=1,h=3*h+1),这种效率比每次取半方式会更高
*/
//Knuth序列的变量h, 其初值为1
int h = 1;
//使用while循环, 判断h是否小于等于数组长度的1/3
while(h <= arr.length/3) {
//若满足条件, 将本轮循环的h值代入该序列, 获取新的h值
h = h*3 + 1;
}
//第一个外层循环
// for (int gap = arr.length/2; gap > 0; gap/=2) {
for (int gap = h; gap > 0; gap/=2) {
//第二个外层循环
for (int i = gap; i < arr.length; i++) {
//希尔排序的内层循环
for (int j = i; j > gap-1 ; j-=gap) {
//判断当前下标的元素值是否小于上一个下标元素
if(arr[j] < arr[j-gap]) {
//若当前元素值小于上一个元素, 则交换两者的值
swap(arr, j,j-gap);
}
}
}
//每轮外层循环结束后, num计数器加1
num++;
//每轮排序结果
System.out.println("间隔为"+gap+"时, 第"+ num +"轮排序结果为:");
//打印排序结果
print(arr);
}
}
/**
* 交换两个元素值
* @param arr 待排序整型数组
* @param i 元素1下标
* @param j 元素2下标
*/
static void swap(int[] arr, int i, int j) {
//首先将i下标元素值赋给temp(临时变量)
int temp = arr[i];
//然后将j下标元素值赋给i下标元素
arr[i] = arr[j];
//最后将temp(临时变量)值赋给j下标元素
arr[j] = temp;
}
/**
* 打印排序结果
* @param arr 待排序整型数组
*/
static void print(int[] arr) {
//for循环遍历数组元素
for (int i = 0; i < arr.length; i++) {
//打印排序后结果
System.out.println(arr[i]+" ");
}
}
}
- 测试结果
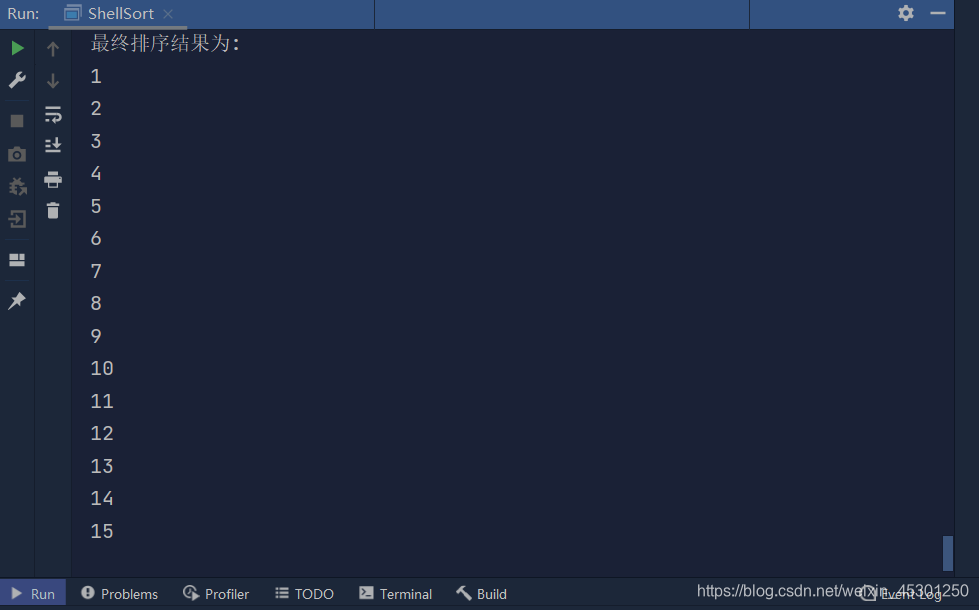
结果:元素从小到大排序,排序结果正确!
1.2.2 使用对数器进行检验
- 测试代码
package com.kuang.test05;
import java.util.Arrays;
import java.util.Random;
public class DataChecker {
//生成随机数组的方法
static int[] generateRandomArray() {
//获取随机数对象
Random ran = new Random();
//创建初始长度为10000的int型数组
int[] arr = new int[100000];
//遍历数组元素
for (int i = 0; i < arr.length; i++) {
//i下标数组元素为随机数的下一个值
arr[i] = ran.nextInt(100000);
}
//将arr随机数组返回
return arr;
}
//检验方法
static void check() {
//创建int型arr数组,其元素由随机数生成器生成
int[] arr = generateRandomArray();
//创建int型arr2数组,其初始大小与arr相同
int[] arr2 = new int[arr.length];
//复制arr的元素到arr2数组中
System.arraycopy(arr, 0, arr2, 0, arr.length);
//使用默认数组方式进行排序
Arrays.sort(arr);
//调用希尔排序算法进行排序
ShellSort.sort(arr2);
//设置标志位初始值为true
boolean flag = true;
//遍历arr2数组元素
for(int i=0; i<arr2.length; i++) {
//判断arr数组和arr2数组的元素是否相同
if(arr[i] != arr2[i])
//若不同,将标志位变为false
flag = false;
}
//标志位是否为true,输出same,否则输出different
System.out.println(false == true? "same":"different");
}
public static void main(String[] args) {
//检查排序结果
check();
}
}
- 测试结果
1.3 希尔排序时间和空间复杂度
1.3.1 希尔排序时间复杂度
- 时间复杂度
希尔排序的时间复杂度为n1.3,最坏时间复杂度为 n2,最好时间复杂度为 n
1.3.2 希尔排序空间复杂度
- 空间复杂度
1.3.3 希尔排序稳定性
由于希尔排序没有出现创建新数组,所以空间复杂度为1
- 稳定性
跳着排序,存在a和b两个值相等时,排序前a在前b在后,排序后b在前a在后,所以不稳定
好了,到这里,今天有关希尔排序算法的学习就结束了,欢迎大家讨论和学习!
参考视频链接:https://www.bilibili.com/video/BV14i4y1T7Af