[数据结构与算法]【算法】动态规划DP自学笔记 入门：基本知识+经典例题

简述

动态规划，是利用历史记录来避免重复计算的一种算法，是求解决策过程最优化的过程。一般用一维数组/二维数组来保存历史记录。
一般动态规划有三个步骤：

1. 定义数组元素的含义，一般求什么就定义成什么
2. 找出数组元素之间的关系式，类似归纳法
3. 找出初始值

例题

1 青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法？

由题意知：青蛙可以从n-1的位置到n，也可以从n-2的位置到n，因此，f(n)=f(n-1)+f(n-2);
初始化：由于变量最小为0,也易得：f(0)=0,f(1)=1,f(2)=2（注意，虽然按照规律，f(2)=f(1)+f(0)=1，但实际并不是这样，要进行特殊处理。）

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1005;
int main()
{
	int n;cin>>n;
	int dp[N];
	dp[0]=0,dp[1]=1,dp[2]=2;
	for(int i=3;i<=n;i++)
	{
		dp[i]=dp[i-1]+dp[i-2];
	}
	cout<<dp[n];
	return 0; 
}

2 二维数组

原题
一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。
问总共有多少条不同的路径？

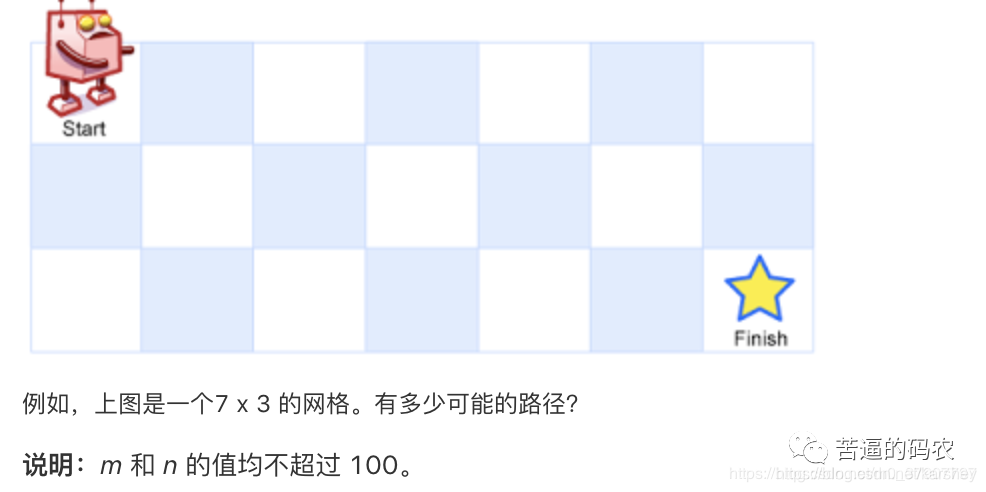
机器只能向下或向右，因此每个位置只能由其左边或上面得来。
dp[i][j]数组的含义就是走到(i,j)的路径数，转移方程就为：

dp[i][j]=dp[i-1][j]+dp[i][j-1];

初始化：dp[0][0]=0（初始位置）,dp[m][0]=1（第一行的都是1，因为只能从左边得来），dp[0][n]（第一列的都是1，只能从上方得来）。

class Solution {
public:
    int uniquePaths(int m, int n) {
        int N=105;
        int dp[N][N];
        dp[0][0]=0;
        for(int i=0;i<m;i++)//lie
        {
            dp[i][0]=1;
        }
        for(int i=0;i<n;i++)
        {
            dp[0][i]=1;
        }
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                dp[i][j]=dp[i-1][j]+dp[i][j-1];
            }
        }
        return dp[m-1][n-1];
    }
};

3 二维数组

原题

只能向下或向右走，因此每个位置只能由上面或左面走来。
第一行的和第一列的要特殊初始化：只能由前面的和当前位置相加得到。
因此，每个位置的dp值为min(上，左)+该位置的值。
即：

for(int i=1;i<m;i++)
    for(int j=1;j<n;j++)
      dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];     

AC：

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m=grid.size(),n=grid[0].size();
        int dp[m][n];
        dp[0][0]=grid[0][0];

        //最左边的和最上面的只能由前一个相加得到
        for(int i=1;i<n;i++)//最上
        {
            dp[0][i]=dp[0][i-1]+grid[0][i];
        }
        for(int i=1;i<m;i++)//最左
        {
            dp[i][0]=dp[i-1][0]+grid[i][0];
        }

        //dp
        for(int i=1;i<m;i++)
        {
            for(int j=1;j<n;j++)
            {
                dp[i][j]=min(dp[i-1][j],dp[i][j-1])+grid[i][j];
            }
        }
        
        return dp[m-1][n-1];
    }
};

参考资料和案例来源

告别动态规划，连刷40道动规算法题，我总结了动规的套路