题目来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems
特别鸣谢:来自夸夸群的 醉笑陪公看落花@知乎,王不懂不懂@知乎,QFIUNE@csdn
感谢醉笑陪公看落花@知乎 倾囊相授,感谢小伙伴们督促学习,一起进步
给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内(可以穿过网格边界到达网格之外)。你 最多 可以移动 maxMove 次球。
给你五个整数 m、n、maxMove、startRow 以及 startColumn ,找出并返回可以将球移出边界的路径数量。因为答案可能非常大,返回对 109 + 7 取余 后的结果。
输入:m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出:6
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/out-of-boundary-paths
题目分析
从起始点开始,有四个方向可以遍历,检查是否越界,如果越界,则路径+1
[0, 1], [0, -1], [1, 0], [-1, 0]
和图的访问有些类似,可以用深度优先遍历找路径,遍历生成的树如下图:
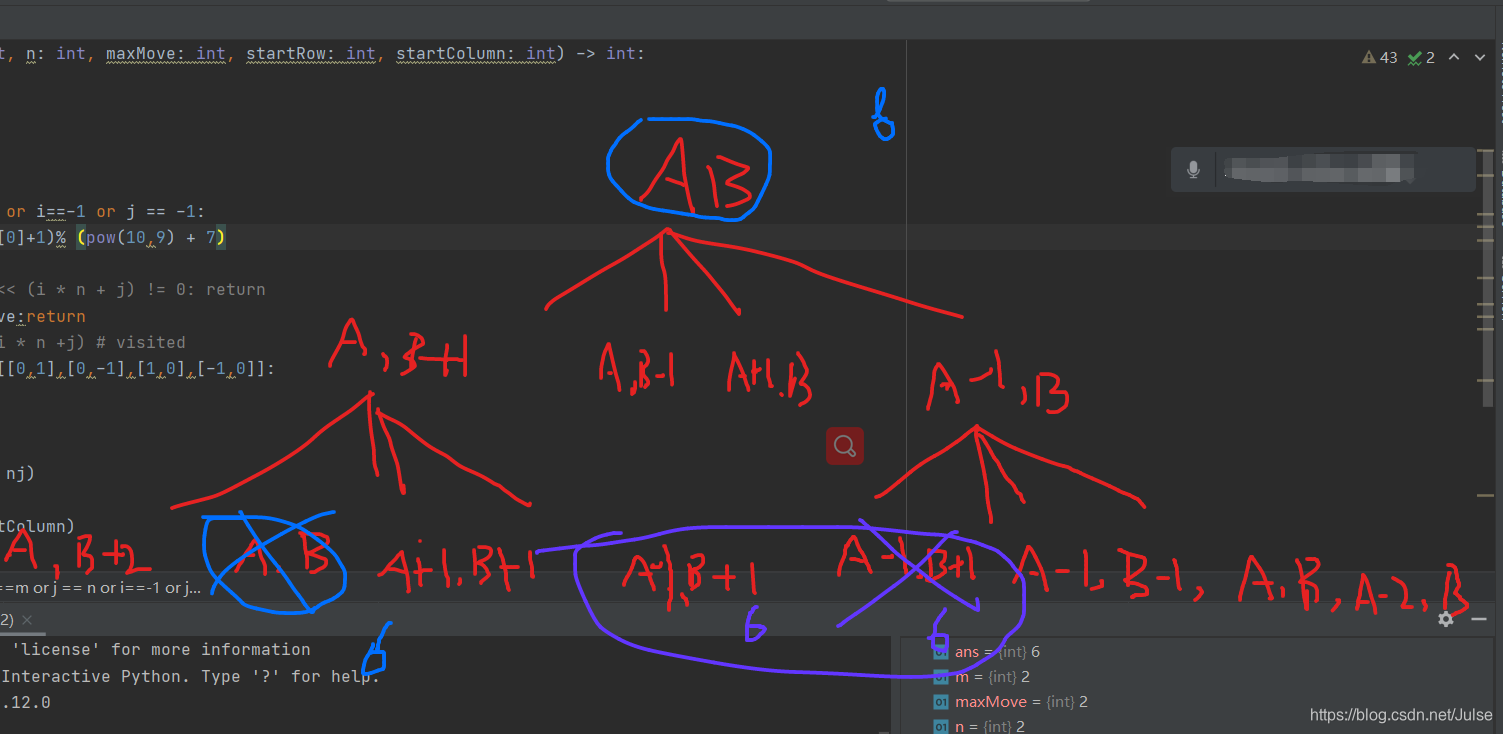
由于题目给了maxMove ,并且可以重复进入同一个坐标位置,不需要设置访问数组,实际move的次数需要记录下来
DFS - 超时
深度优先从一个位置出发,进行遍历和检查。
用一个全局变量来累加出界的情况
'''
超时
'''
class Solution:
def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
# mask = [0]
ans = [0]
move = [0]
# i 行 j 列: i * n +j
def DFS(m,n,i,j):
if i==m or j == n or i==-1 or j == -1:
ans[0] = (ans[0]+1)% (pow(10,9) + 7)
return
# if mask[0] & 1 << (i * n + j) != 0: return
if move[0]>=maxMove:return
# mask[0] |= 1<<(i * n +j) # visited
for diri,dirj in [[0,1],[0,-1],[1,0],[-1,0]]:
ni =i+diri
nj =j+dirj
move[0] += 1
DFS(m, n, ni, nj)
move[0] -= 1
DFS(m,n,startRow,startColumn)
return ans[0]
DFS-字典实现备忘录-通过
这棵树的某些结点完全一样,可以进行剪枝优化
使用备忘录需要DFS有返回值,下次输入相同的参数,直接返回备忘录中记录的返回值即可。
上面的解题方式是直接修改的全局变量,没有返回值,需要做一些修改,重新定义DFS含义,
DFS(m,n,i,j,move) 表示题目的一个子问题,从i j 开始出发,最多移动move次可以越界的路径数
'''
通过
'''
class Solution:
def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
memor = {}
def DFS(m,n,i,j,move):
if (i,j,move) in memor: return memor[(i,j,move)]
if move == -1:return 0
if i==m or j == n or i==-1 or j == -1:
return 1
ans = 0
for diri,dirj in [[0,1],[0,-1],[1,0],[-1,0]]:
ni =i+diri
nj =j+dirj
ans += DFS(m, n, ni, nj,move-1)
memor[(i, j, move)] = ans % (pow(10,9) + 7)
return ans % (pow(10,9) + 7)
return DFS(m,n,startRow,startColumn,maxMove)
DFS- 库函数实现备忘录-通过
'''
通过
'''
import functools
class Solution:
def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
# i 行 j 列: i * n +j
@functools.lru_cache(None)
def DFS(m,n,i,j,move):
if move == -1:return 0
if i==m or j == n or i==-1 or j == -1:
return 1
ans = 0
for diri,dirj in [[0,1],[0,-1],[1,0],[-1,0]]:
ni =i+diri
nj =j+dirj
ans += DFS(m, n, ni, nj,move-1)
return ans % (pow(10,9) + 7)
return DFS(m,n,startRow,startColumn,maxMove)
DFS - 库函数 - 推导式 - 通过
'''
推导式
'''
import functools
class Solution:
def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
@functools.lru_cache(None)
def DFS(m,n,i,j,move):
return 0 if move == -1 else 1 if i==m or j == n or i==-1 or j == -1 else (sum([DFS(m, n, i+1, j,move-1),DFS(m, n, i-1, j,move-1),DFS(m, n, i, j+1,move-1),DFS(m, n, i, j-1,move-1)]))% (pow(10,9) + 7)
return DFS(m,n,startRow,startColumn,maxMove)
动态规划 - 通过
'''
动态规划
'''
class Solution:
def findPaths(self, m: int, n: int, maxMove: int, startRow: int, startColumn: int) -> int:
maxMove+=1
dp = [[[0]*maxMove for _ in range(n+2)] for _ in range(m+2)]
for i in range(m+2):
for j in range(maxMove):
dp[i][0][j] = dp[i][n+1][j] = 1
for i in range(n+2):
for j in range(maxMove):
dp[0][i][j] = dp[m+1][i][j] = 1
for mm in range(1, maxMove):
for i in range(1,m+1):
if mm == maxMove-1 and i>startRow+1:break
for j in range(1,n+1):
if mm == maxMove - 1 and j > startColumn + 1: break
for diri, dirj in [[0, 1], [0, -1], [1, 0], [-1, 0]]:
dp[i][j][mm] += dp[i+diri][j+dirj][mm-1]
dp[i][j][mm] %= (pow(10, 9) + 7)
return (dp[startRow+1][startColumn+1][maxMove-1])
运行效果