什么是哈希
你可能会觉得这个名字很奇怪,或者你可能以为这是某个外国大佬的名字,实际上不是,哈希来自音译Hash,意为散列,就是将一堆比较分散的数据通过某种映射关系集中起来。
一、哈希函数
上面我们所说的某种映射关系实际上还有一种别的名称,就是哈希函数。而不同的哈希函数通常拥有自己的名字。
1.直接法
如果我想存储一些不重复的数字,而这些数字的范围不太大,所有的数字都是1~99之内的,那么我就可以使用直接法。这个名字就很直接,我直接开一个100个int大小的数组,然后从1到99,只要有数字出现,那么我就标记那个位置,这样我们只要去找它对应位置的值是否存在,就能够找到key。
2.余数法
但是,直接法的缺陷也很致命——如果这些数字的范围太大,那么就会导致空间的严重浪费。比如前几个数字都是10以内的,突然来了一个100000,那么我难道要开辟100000个空间吗?所以我们常使用的哈希函数还是余数法。给定一定范围的空间,将key值取余然后映射到这个范围。

上面的图就是一个余数法的栗子,整个空间大小为10,然后key通过取余映射到对应位置,只不过上面的数字都在0 - 9内,所以取不取余数无所谓。那么,接下来我要问的是,如果我再插入一个11呢?好,你可能会说,取余映射不就好了?11 % 10 == 1,但是你发现1的位置已经被占了。这也是我们接下来要讨论的问题,哈希冲突。
哈希冲突
哈希冲突是哈希表逃不过的问题。这个问题来自哈希表本身的定义,将大范围的value通过key值映射到一小块空间。这种化大为小的妙诀自然要付出一定的代价,比如哈希冲突。这也与我们人类社会一样,如果太过拥挤,就一定会有磕磕碰碰。所谓哈希冲突,简言之就是不同的value映射到同一位置,这是可能的,虽然它们的key值不同,但是取余之后就可能相同。接下来为大家介绍两种解决哈希冲突的方法。
1, 闭散列表
这第一种方法的思想就是,你既然知道有人把位置占用了,你用顺延一位,去占用你后面的位置。化成图就是这样的,

这种方法有好处,那自然是解决了哈希冲突,但是缺陷也很明显——那万一key取余后为2的value来了,就又得顺延。最后不妨设想最坏的情况(我认为这种情况会经常发生),所有的位置都错乱了,然后自然地查找效率就会损失,这与我们研究哈希表的意愿背道而驰。总而言之,这种符合我们最初想法的做法应该实现一下。但是,实现闭散列之前,有一个问题,这个问题最终会导致闭散列的结构。如何在一个闭散列哈希表中查找数据呢? 你可能会说,这还不简单,找到key取余之后位置,然后将值取出来不久可以了。如果不是,那就顺着往后找,直到找到不久ok?问题就出现在这,我们遇到空值会停止查找,万一中间有某个值被删除了呢?

33映射到3的位置,21顺延映射到8的位置。然后删除33,现在我想找到21,我先找到1的位置,然后往后找,找到3,发现位置是空,查找结束。很明显,这不是我们想要的,因为3的位置以前有数据,只是被删除了,而非一开始就是空的。所以我们需要将这两种状态区分开来,这也是闭散列哈希表的巧妙结构。还有就是,如果表满了怎么办呢?我们的做法保证了表不会满,引入了负载因子来衡量表满的程度,负载因子就是表中的数据 / 表的大小,如果负载因子过大,就扩大表的容量。
//状态,用来标记当前位置是存在数据,还是从前存在但是被删除了,还是一开始就没有数据。
enum state {
EMPTY,
EXIST,
DELETE,
};
//哈希表的数据类型
template<typename T>
struct __hash_data {
T _data; //数据域
state _state; //状态
__hash_data() :_state(EMPTY) {} //默认的构造函数需要给空,必须给空。
__hash_data(const T& data) :_data(data) {}
};
// 4个模板参数,K就是key的type,T就是value的type,KeyOfT取出value中的key值,Hash是哈希算法
template<typename K, typename T, typename KeyOfT, typename Hash>
class HashTable {
public:
using HashType = __hash_data<T>;
void insert(const T& d) {
KeyOfT koft;
//调整负载因子,如果表为空或者负载因子大于等于0.7,那么需要扩容
if (_tables.size() == 0 || _nums * 10 / _tables.size() > 7) {
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
HashTable<K, T, KeyOfT, Hash> _HT; //这里创建再一个哈希表,复用insert,现代写法
_HT._tables.resize(newSize); //细节,开好空间
for (size_t i = 0; i < _tables.size(); ++i) {
if (_tables[i]._state == EXIST) {
_HT.insert(_tables[i]._data);
}
}
_tables.swap(_HT._tables);
}
//找到映射位置
size_t index = HashFunc(koft(d)) % _tables.size();
while (_tables[index]._state == EXIST) { //直到某个位置的状态是删除或者是空
++index;
if (index == _tables.size()) //如果走到表尾,转到表头
index = 0;
}
_tables[index] = d;
_tables[index]._state = EXIST;
++_nums;
}
HashType* find(const K& key) {
KeyOfT koft;
size_t index = HashFunc(key) % _tables.size();
while (_tables[index]._state != EMPTY) { //状态为存在或者删除都要继续找
if (koft(_tables[index]._data) == key) { //找到key值
if (_tables[index]._state == EXIST) { //如果状态为存在,直接返回
return &_tables[index];
}
else { //如果状态为删除,继续向后找
++index;
if (index == _tables.size())
index = 0;
}
}
}
return nullptr; //没有找到
}
void erase(const K& key) {
HashType* ret = find(key);
if (ret) {
ret->_state = DELETE;
--_nums;
}
else {
return;
}
}
private:
vector<HashType> _tables;
size_t _nums = 0; //表中存入的数据个数
size_t HashFunc(const K& key) { //哈希算法,具体介绍在后面。
return Hash()(key);
}
};
2 ,开散列表
考虑到闭散列的缺陷,后面如我们所愿的出现了一种新的哈希表,开散列。闭散列的冲突是去占用别人的位置,这样于情于理都不太合适。而开散列则是利用链表,如果冲突,那么将冲突的数据挂起来,形成一条一条的链子。
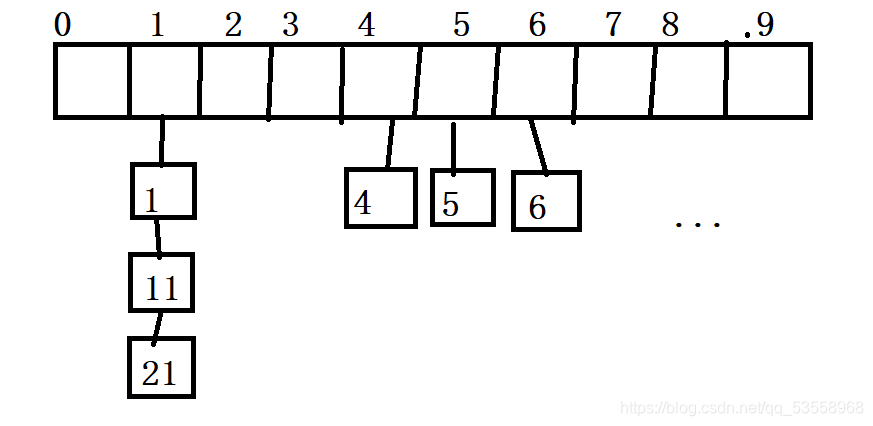
像上面那样。这种方法保证了哈希冲突的解决不去占用别人的资源,而且理应如此。
template<class T>
class _hash {
public:
size_t operator()(const T& data) {
return data;
}
};
// BKDR哈希
template<>
class _hash<string> {
public:
size_t operator()(const string& str) {
size_t hashCode = 0;
for (auto& e : str) {
hashCode = e * 131 + hashCode;
}
return hashCode;
}
};
template<class T>
struct __open_hash_data { //开散列数据类型
T _data;
__open_hash_data* _next;
__open_hash_data():_next(nullptr) {}
__open_hash_data(const T& data):_data(data) {}
};
template<class K, class T, class KeyOfT, class Hash>
class oHashTable {
public:
using HashData = __open_hash_data<T>;
bool insert(const T& d) {
KeyOfT koft;
//调整负载因子,负载因子大于等于1
if (_tables.size() == 0 || _nums * 10 / _tables.size() >= 10) {
size_t newSize = _tables.size() == 0 ? 10 : _tables.size() * 2;
vector<HashData*> newTables;
newTables.resize(newSize);
for (size_t i = 0; i < _tables.size(); ++i) { //遍历整张表
HashData* cur = _tables[i];
HashData* next = nullptr;
while (cur) { //完成一条链子上的节点转移
next = cur->_next;
size_t index = HashFunc(koft(cur->_data)) % newTables.size(); //找到映射位置
cur->_next = newTables[index]; //链接到新表上
newTables[index] = cur;
cur = next;
}
_tables[i] = nullptr; //旧表变空
}
_tables.swap(newTables);
}
size_t index = HashFunc(koft(d)) % _tables.size();
HashData* cur = _tables[index];
while (cur) {
if (cur->_data == d) {
return false;
}
else {
cur = cur->_next;
}
}
HashData* newData = new HashData(d);
newData->_next = _tables[index];
_tables[index] = newData;
++_nums;
return true;
}
HashData* find(const K& key) {
KeyOfT koft;
size_t index = HashFunc(key) % _tables.size();
HashData* cur = _tables[index];
while (cur && koft(cur->_data) != key) {
cur = cur->_next;
}
return cur;
}
bool erase(const K& key) {
KeyOfT koft;
size_t index = HashFunc(key) % _tables.size();
HashData* cur = _tables[index], prev = nullptr;
while (cur) {
if (koft(cur->_data) == key) { //找到要删除的value
if (prev == nullptr) { //如果头节点要删除
_tables[index] = cur->_next;
delete cur;
}
else {
prev->_next = cur->_next;
delete cur;
}
--_nums;
return true;
}
else { //没有找到
prev = cur;
cur = cur->_next;
}
}
//如果运行到这,说明没有找到
return false;
}
private:
vector<HashData*> _tables;
size_t _nums = 0;
size_t HashFunc(const K& key) {
return Hash()(key);
}
};
字符串哈希算法
字符串哈希算法就是将字符串转换成可以取余的整形的函数,给大家贴上一个网站,自行参考。
字符串哈希算法
iterator
哈希表的iterator有点意思。iterator其实封装的是哈希节点的指针。我就operator++说一说,如果当前节点的next指针非空,那么直接返回next构造的迭代器就行。如果next为空,那么重点来了。我们要找到下一个位置,我们需要哈希表的信息,所以哈希表迭代器还应该封装一个哈希表的成员。
template<class K, class T, class KeyOfT, class Hash> //前置声明
class oHashTable;
template<class T>
struct __open_hash_data;
template<class K, class T, class KeyOfT, class Hash>
struct _HashTableIterator {
using HashData = __open_hash_data<T>;
using HT = oHashTable<K, T, KeyOfT, Hash>; //哈希表
using Self = _HashTableIterator<K, T, KeyOfT, Hash>;
HashData* _node;
HT* _ht;
_HashTableIterator(HashData* node, HT* ht):_node(node),_ht(ht) {}
T& operator*() {
return _node->_data;
}
T* operator->() {
return &operator*();
}
Self operator++() {
if (_node->_next) { //这条链子上非空
_node = _node->_next;
return *this;
}
else { //此条链子后面已经没有节点了
size_t index = _ht->HashFunc(KeyOfT()(_node->_data)) % _ht->_tables.size();
++index;
for (; index < _ht->_tables.size(); ++index) {
if (_ht->_tables[index]) {
_node = _ht->_tables[index];
return *this;
}
}
}
//后面没有节点了
_node = nullptr;
return *this;
}
unordered_set
所谓unordered系列,其实就是封装了哈希表,所用的方法与set和map封装红黑树大抵相同,实现起来也相当简单。
template<class K>
class SetKOfT {
public:
const K& operator()(const K& key) {
return key;
}
};
template<class K, class Hash = _hash<K>>
class Myunordered_set {
public:
using HT = oHashTable<K, K, SetKOfT<K>, Hash>;
using iterator = typename HT::iterator;
iterator begin() {
return _ht.begin();
}
iterator end() {
return _ht.end();
}
pair<iterator, bool> insert(const K& key) {
return _ht.insert(key);
}
void erase(const K& key) {
return _ht.erase(key);
}
private:
HT _ht;
};
unordered_map
template<class K, class V>
class MapKeyOfT {
public:
const K& operator()(const pair<K, V>& kv) {
return kv.first;
}
};
template<class K, class V, class Hash = _hash<K>>
class Myunordered_map {
public:
using HT = oHashTable<K, pair<K, V>, MapKeyOfT<K, V>, Hash>;
using iterator = typename HT::iterator;
iterator begin() {
return _ht.begin();
}
iterator end() {
return _ht.end();
}
pair<iterator, bool> insert(const pair<K, V>& kv) {
return _ht.insert(kv);
}
V& operator[](const K& key) {
iterator ret = _ht.insert(make_pair(key, V())).first;
return (*ret).second;
}
private:
HT _ht;
};