[数据结构与算法]哪两种遍历方式可以唯一确定一棵二叉树结合力扣105题

对于一棵树的前中序三种顺序的遍历方式，任何一种单独拿出来都无法确定一棵树，那么两种遍历方式得到的节点数据能否构建一棵二叉树呢？
先来看看能有哪几种组合：

1. 先序遍历 + 中序遍历
2. 后序遍历 + 中序遍历
3. 先序遍历 + 后续遍历（不可行）

以上三种组合都可以组成二叉树，但是只有前两种组合可以唯一确定一棵二叉树，最后一种也就是先序遍历 + 后序遍历无法唯一确定一棵二叉树。为什么呢?
下给出一棵树的前中后序遍历：
先序遍历：A B D H L E C F I J M N G K
中序遍历：D H L B E A I F N M J C G K
后序遍历：L H D E B I N M J F K G C A
我们要从以上数据中的到什么样的信息才能组成一棵二叉树？
答案是节点的顺序。
我们怎么能知道顺序呢？
先序和后序可以告诉我们根节点，只不过先序遍历的根节点从前往后，后序遍历的根节点从后往前，也正是因为先序遍历和后序遍历都只能告诉我们根节点这个信息，所以他们两个在一起是没办法得到足够信息去构建二叉树的。我们知道根节点之后，可以拿这个根节点在中序遍历的数据中，以该节点为中心，节点左面为该节点的左子树，节点右面为该节点的右子树。很明显上述的规律有递归的特性。
从上面的叙述中可以得知，先序遍历和后序遍历对于我们组建一个二叉树所能提供的信息都只是根节点，我们依次拿着根节点去中序遍历分割左子树和右子树，在通过递归组成整颗树。
拿例子中的树来验证上述：

1. 先从先序遍历中拿出根节点A，去中序遍历分割左右子树。

2. 拿出先序遍历的下个节点B，去1中分割好的A的左子树中去分割

3. 拿着先序遍历的下个节点D,去2中分割好的左子树中去分割

4. 拿着先序遍历的下个节点H去3中分割好的左子树，不对3中根节点没有左子树，根据遍历的特点H为D的右子树中的节点，

至此A的左子树全部分割结束，可以根据上面几点画出A的左子树。

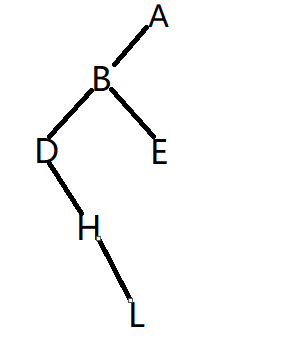
再用同样的方法在先序遍历中取根节点，在中序遍历分割好的A的右子树中去依次分割，最终可以画出整颗树如下图：

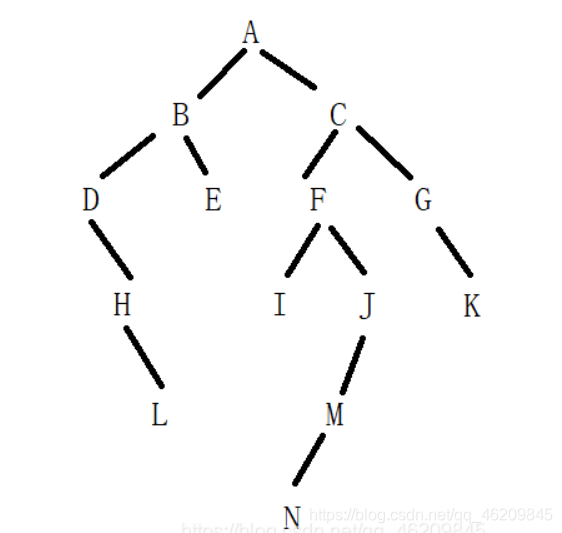
LeetCode105： 从前序与中序遍历序列构造二叉树
下面通过代码来运用上述观点：

package leetcode.p105;

import leetcode.TreeNode;

import java.util.Arrays;

public class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
    	//递归出口
        if (preorder.length == 0) {
            return null;
        }

        int rootValue = preorder[0];
        TreeNode root = new TreeNode(rootValue);
        // 左子树的结点个数?
        int leftSize = 0;
        for (int i = 0; i < inorder.length; i++) {
            if (inorder[i] == rootValue) {
                leftSize = i;
            }
        }
        int rightSize = inorder.length - leftSize - 1;

        // 左子树的前序和中序
        int[] leftPreorder = Arrays.copyOfRange(preorder, 1, 1 + leftSize);
        int[] leftInorder = Arrays.copyOfRange(inorder, 0, leftSize);
        root.left = buildTree(leftPreorder, leftInorder);

        // 右子树的前序和中序
        int[] rightPreorder = Arrays.copyOfRange(preorder, 1 + leftSize, preorder.length);
        int[] rightInorder = Arrays.copyOfRange(inorder, leftSize + 1, inorder.length);
        root.right = buildTree(rightPreorder, rightInorder);

        return root;
    }
}

虽然上面代码不是最优解，但是在我看来是最方便理解
前序遍历 + 中序遍历可以构建一棵二叉树的代码。
后序遍历 + 中序遍历同理，只不过后序遍历根节点从后往前。