目录
回归分析的定义
回归分析是一种预测性的建模技术,它研究的是因变量(目标)和自变量(预测器)之间的关系。这种技术通常用于预测分析,时间序列模型以及发现变量之间的因果关系。例如,司机的鲁莽驾驶与道路交通 事 故数量之间的关系,最好的研究方法就是回归。
回归分析是建模和分析数据的重要工具。在这里,我们使用曲线/线来拟合这些数据点,在这种方式下,从曲线或线到数据点的距离差异最小。我会在接下来的部分详细解释这一点。
简单来说,Regression 就是找到一个函数?functionfunction?,通过输入特征?xx,输出一个数值?ScalarScalar。

回归应用举例
- 股市预测(Stock market forecast)
- 输入:过去10年股票的变动、新闻咨询、公司并购咨询等
- 输出:预测股市明天的平均值
- 自动驾驶(Self-driving Car)
- 输入:无人车上的各个sensor的数据,例如路况、测出的车距等
- 输出:方向盘的角度
- 商品推荐(Recommendation)
- 输入:商品A的特性,商品B的特性
- 输出:购买商品B的可能性
- Pokemon精灵攻击力预测(Combat Power of a pokemon):
- 输入:进化前的CP值、物种(Bulbasaur)、血量(HP)、重量(Weight)、高度(Height)
- 输出:进化后的CP值
 ?
?
七种常见的回归
1. Linear Regression线性回归
它是最为人熟知的建模技术之一。线性回归通常是人们在学习预测模型时首选的技术之一。在这种技术中,因变量是连续的,自变量可以是连续的也可以是离散的,回归线的性质是线性的。
线性回归使用最佳的拟合直线(也就是回归线)在因变量(Y)和一个或多个自变量(X)之间建立一种关系。
用一个方程式来表示它,即Y=a+b*X + e,其中a表示截距,b表示直线的斜率,e是误差项。这个方程可以根据给定的预测变量(s)来预测目标变量的值。
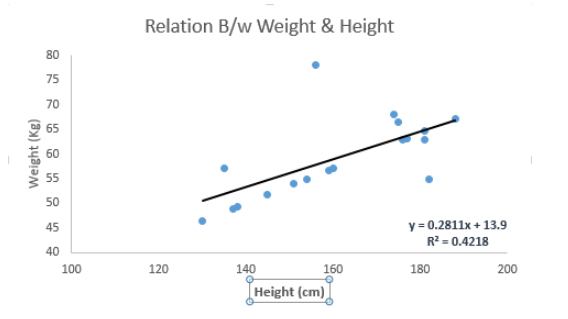
一元线性回归和多元线性回归的区别在于,多元线性回归有(>1)个自变量,而一元线性回归通常只有1个自变量。现在的问题是“我们如何得到一个最佳的拟合线呢?”。
如何获得最佳拟合线(a和b的值)?
这个问题可以使用最小二乘法轻松地完成。最小二乘法也是用于拟合回归线最常用的方法。对于观测数据,它通过最小化每个数据点到线的垂直偏差平方和来计算最佳拟合线。因为在相加时,偏差先平方,所以正值和负值没有抵消。
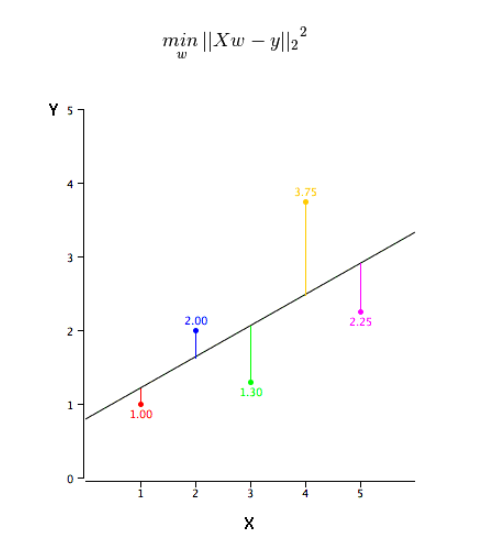
我们可以使用R-square指标来评估模型性能。想了解这些指标的详细信息,可以阅读:模型性能指标Part 1,Part 2 .
要点:
-
自变量与因变量之间必须有线性关系
-
多元回归存在多重共线性,自相关性和异方差性。
-
线性回归对异常值非常敏感。它会严重影响回归线,最终影响预测值。
-
多重共线性会增加系数估计值的方差,使得在模型轻微变化下,估计非常敏感。结果就是系数估计值不稳定
-
在多个自变量的情况下,我们可以使用向前选择法,向后剔除法和逐步筛选法来选择最重要的自变量。
?
2.Logistic Regression逻辑回归
逻辑回归是用来计算“事件=Success”和“事件=Failure”的概率。当因变量的类型属于二元(1 / 0,真/假,是/否)变量时,我们就应该使用逻辑回归。这里,Y的值从0到1,它可以用下方程表示。
Java
| 1 2 3 | odds=?p/?(1-p)?=?probability?of?event?occurrence?/?probability?of?not?event?occurrence ln(odds)?=?ln(p/(1-p)) logit(p)?=?ln(p/(1-p))?=?b0+b1X1+b2X2+b3X3....+bkXk |
上述式子中,p表述具有某个特征的概率。你应该会问这样一个问题:“我们为什么要在公式中使用对数log呢?”。
因为在这里我们使用的是的二项分布(因变量),我们需要选择一个对于这个分布最佳的连结函数。它就是Logit函数。在上述方程中,通过观测样本的极大似然估计值来选择参数,而不是最小化平方和误差(如在普通回归使用的)。

要点:
-
它广泛的用于分类问题。
-
逻辑回归不要求自变量和因变量是线性关系。它可以处理各种类型的关系,因为它对预测的相对风险指数OR使用了一个非线性的log转换。
-
为了避免过拟合和欠拟合,我们应该包括所有重要的变量。有一个很好的方法来确保这种情况,就是使用逐步筛选方法来估计逻辑回归。
-
它需要大的样本量,因为在样本数量较少的情况下,极大似然估计的效果比普通的最小二乘法差。
-
自变量不应该相互关联的,即不具有多重共线性。然而,在分析和建模中,我们可以选择包含分类变量相互作用的影响。
-
如果因变量的值是定序变量,则称它为序逻辑回归。
-
如果因变量是多类的话,则称它为多元逻辑回归。
3. Polynomial Regression多项式回归
对于一个回归方程,如果自变量的指数大于1,那么它就是多项式回归方程。如下方程所示:
在这种回归技术中,最佳拟合线不是直线。而是一个用于拟合数据点的曲线。

重点:
虽然会有一个诱导可以拟合一个高次多项式并得到较低的错误,但这可能会导致过拟合。你需要经常画出关系图来查看拟合情况,并且专注于保证拟合合理,既没有过拟合又没有欠拟合。下面是一个图例,可以帮助理解:
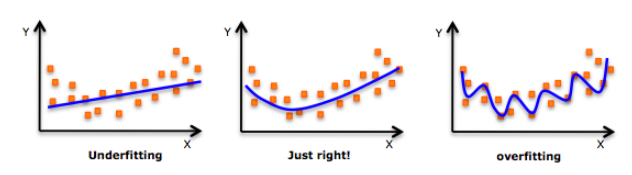
明显地向两端寻找曲线点,看看这些形状和趋势是否有意义。更高次的多项式最后可能产生怪异的推断结果。
?
4. Stepwise Regression逐步回归
在处理多个自变量时,我们可以使用这种形式的回归。在这种技术中,自变量的选择是在一个自动的过程中完成的,其中包括非人为操作。
这一壮举是通过观察统计的值,如R-square,t-stats和AIC指标,来识别重要的变量。逐步回归通过同时添加/删除基于指定标准的协变量来拟合模型。下面列出了一些最常用的逐步回归方法:
-
标准逐步回归法做两件事情。即增加和删除每个步骤所需的预测。
-
向前选择法从模型中最显著的预测开始,然后为每一步添加变量。
-
向后剔除法与模型的所有预测同时开始,然后在每一步消除最小显着性的变量。
这种建模技术的目的是使用最少的预测变量数来最大化预测能力。这也是处理高维数据集的方法之一。
5. Ridge Regression岭回归
岭回归分析是一种用于存在多重共线性(自变量高度相关)数据的技术。在多重共线性情况下,尽管最小二乘法(OLS)对每个变量很公平,但它们的差异很大,使得观测值偏移并远离真实值。岭回归通过给回归估计上增加一个偏差度,来降低标准误差。
上面,我们看到了线性回归方程。还记得吗?它可以表示为:
这个方程也有一个误差项。完整的方程是:
Java
| 1 | y=a+b*x+e?(error?term),?[error?term?is?the?value?needed?to?correct?for?a?prediction?error?between?the?observed?and?predicted?value] |
Java
| 1 | =>?y=a+y=?a+?b1x1+?b2x2+....+e,?for?multiple?independent?variables. |
在一个线性方程中,预测误差可以分解为2个子分量。一个是偏差,一个是方差。预测错误可能会由这两个分量或者这两个中的任何一个造成。在这里,我们将讨论由方差所造成的有关误差。
岭回归通过收缩参数λ(lambda)解决多重共线性问题。看下面的公式

在这个公式中,有两个组成部分。第一个是最小二乘项,另一个是β2(β-平方)的λ倍,其中β是相关系数。为了收缩参数把它添加到最小二乘项中以得到一个非常低的方差。
要点:
-
除常数项以外,这种回归的假设与最小二乘回归类似;
-
它收缩了相关系数的值,但没有达到零,这表明它没有特征选择功能
-
这是一个正则化方法,并且使用的是L2正则化。
?
6. Lasso Regression套索回归
它类似于岭回归,Lasso (Least Absolute Shrinkage and Selection Operator)也会惩罚回归系数的绝对值大小。此外,它能够减少变化程度并提高线性回归模型的精度。看看下面的公式:
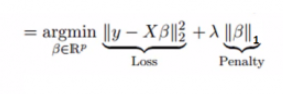
Lasso 回归与Ridge回归有一点不同,它使用的惩罚函数是绝对值,而不是平方。这导致惩罚(或等于约束估计的绝对值之和)值使一些参数估计结果等于零。使用惩罚值越大,进一步估计会使得缩小值趋近于零。这将导致我们要从给定的n个变量中选择变量。
要点:
-
除常数项以外,这种回归的假设与最小二乘回归类似;
-
它收缩系数接近零(等于零),这确实有助于特征选择;
-
这是一个正则化方法,使用的是L1正则化;
如果预测的一组变量是高度相关的,Lasso 会选出其中一个变量并且将其它的收缩为零。
7.ElasticNet回归
ElasticNet是Lasso和Ridge回归技术的混合体。它使用L1来训练并且L2优先作为正则化矩阵。当有多个相关的特征时,ElasticNet是很有用的。Lasso 会随机挑选他们其中的一个,而ElasticNet则会选择两个。

Lasso和Ridge之间的实际的优点是,它允许ElasticNet继承循环状态下Ridge的一些稳定性。
要点:
-
在高度相关变量的情况下,它会产生群体效应;
-
选择变量的数目没有限制;
-
它可以承受双重收缩。
除了这7个最常用的回归技术,你也可以看看其他模型,如Bayesian、Ecological和Robust回归。
三种常用的损失函数
1、SSE(误差平方和)?The sum of squares due to error
计算公式如下:
? ? ?
同样的数据集的情况下,SSE越小,误差越小,模型效果越好
缺点:
SSE数值大小本身没有意义,随着样本增加,SSE必然增加,也就是说,不同的数据集的情况下,SSE比较没有意义
2、R-square(决定系数) Coefficient of determination
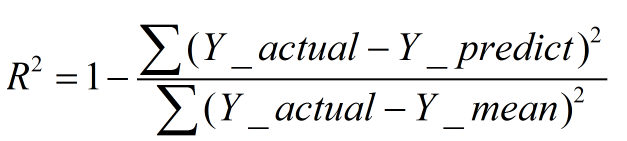
数学理解: 分母理解为原始数据的离散程度,分子为预测数据和原始数据的误差,二者相除可以消除原始数据离散程度的影响
其实“决定系数”是通过数据的变化来表征一个拟合的好坏。
理论上取值范围(-∞,1], 正常取值范围为[0 1] ------实际操作中通常会选择拟合较好的曲线计算R2,因此很少出现-∞
一个常数模型总是预测 y 的期望值,它忽略输入的特征,因此输出的R^2会为0
越接近1,表明方程的变量对y的解释能力越强,这个模型对数据拟合的也较好
越接近0,表明模型拟合的越差
经验值:>0.4, 拟合效果好
缺点:
数据集的样本越大,R2越大,因此,不同数据集的模型结果比较会有一定的误差
3、Adjusted R-Square (校正决定系数)Degree-of-freedom adjusted coefficient of determination
? ?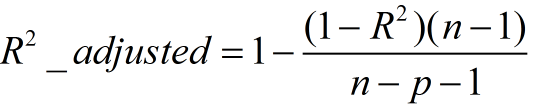
n为样本数量,p为特征数量
消除了样本数量和特征数量的影响
python中的sklearn. metrics?
python的sklearn.metrics中包含一些损失函数,评分指标来评估回归模型的效果。主要包含以下几个指标:n_squared_error, mean_absolute_error, explained_variance_score and r2_score.。
(1) explained_variance_score(解释方差分)
? ?y_hat :预测值, y :真实值, var :方差
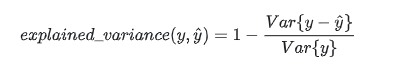
explained_variance_score:解释方差分,这个指标用来衡量我们模型对数据集波动的解释程度,如果取值为1时,模型就完美,越小效果就越差。下面是python的使用情况:
# 解释方差分数
>>> from sklearn.metrics import explained_variance_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> explained_variance_score(y_true, y_pred) ?
0.957...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> explained_variance_score(y_true, y_pred, multioutput='raw_values')
...?
array([ 0.967..., ?1. ? ? ? ?])
>>> explained_variance_score(y_true, y_pred, multioutput=[0.3, 0.7])
...?
0.990...
(2) Mean absolute error(平均绝对误差)
? ?y_hat :预测值, y :真实值
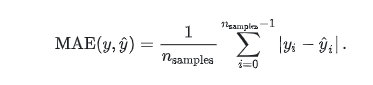
给定数据点的平均绝对误差,一般来说取值越小,模型的拟合效果就越好。下面是在python上的实现:
>>> from sklearn.metrics import mean_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_absolute_error(y_true, y_pred)
0.5
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_absolute_error(y_true, y_pred)
0.75
>>> mean_absolute_error(y_true, y_pred, multioutput='raw_values')
array([ 0.5, ?1. ])
>>> mean_absolute_error(y_true, y_pred, multioutput=[0.3, 0.7])
...?
0.849...
(3)Mean squared error(均方误差)
? ?y_hat :预测值, y :真实值
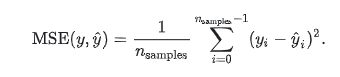
这是人们常用的指标之一。
>>> from sklearn.metrics import mean_squared_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> mean_squared_error(y_true, y_pred)
0.375
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> mean_squared_error(y_true, y_pred) ?
0.7083...
(4) Mean squared logarithmic error
? ?y_hat :预测值, y :真实值

? ? ?当目标实现指数增长时,例如人口数量、一种商品在几年时间内的平均销量等,这个指标最适合使用。请注意,这个指标惩罚的是一个被低估的估计大于被高估的估计。
>>> from sklearn.metrics import mean_squared_log_error
>>> y_true = [3, 5, 2.5, 7]
>>> y_pred = [2.5, 5, 4, 8]
>>> mean_squared_log_error(y_true, y_pred) ?
0.039...
>>> y_true = [[0.5, 1], [1, 2], [7, 6]]
>>> y_pred = [[0.5, 2], [1, 2.5], [8, 8]]
>>> mean_squared_log_error(y_true, y_pred) ?
0.044...
(5)Median absolute error(中位数绝对误差)
y_hat :预测值, y :真实值
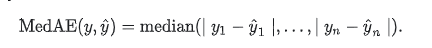
中位数绝对误差适用于包含异常值的数据的衡量
>>> from sklearn.metrics import median_absolute_error
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> median_absolute_error(y_true, y_pred)
0.5
(6) R2 score(决定系数、R方)

R方可以理解为因变量y中的变异性能能够被估计的多元回归方程解释的比例,它衡量各个自变量对因变量变动的解释程度,其取值在0与1之间,其值越接近1,则变量的解释程度就越高,其值越接近0,其解释程度就越弱。
一般来说,增加自变量的个数,回归平方和会增加,残差平方和会减少,所以R方会增大;反之,减少自变量的个数,回归平方和减少,残差平方和增加。
为了消除自变量的数目的影响,引入了调整的R方
?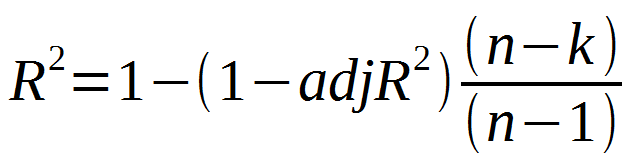
>>> from sklearn.metrics import r2_score
>>> y_true = [3, -0.5, 2, 7]
>>> y_pred = [2.5, 0.0, 2, 8]
>>> r2_score(y_true, y_pred) ?
0.948...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='variance_weighted')
...?
0.938...
>>> y_true = [[0.5, 1], [-1, 1], [7, -6]]
>>> y_pred = [[0, 2], [-1, 2], [8, -5]]
>>> r2_score(y_true, y_pred, multioutput='uniform_average')
...?
0.936...
>>> r2_score(y_true, y_pred, multioutput='raw_values')
...?
array([ 0.965..., ?0.908...])
>>> r2_score(y_true, y_pred, multioutput=[0.3, 0.7])
...?
0.925...在python上实现交叉验证
############################交叉验证,评价模型的效果############################
from sklearn import datasets, linear_model
from sklearn.model_selection import cross_val_score
diabetes = datasets.load_diabetes()
X = diabetes.data[:150]
y = diabetes.target[:150]
lasso = linear_model.Lasso()
print(cross_val_score(lasso, X, y, cv=5)) ?# 默认是3-fold cross validation############################交叉验证,评价模型的效果############################
from sklearn import datasets, linear_model
from sklearn.model_selection import cross_val_score
diabetes = datasets.load_diabetes()
X = diabetes.data[:150]
y = diabetes.target[:150]
lasso = linear_model.Lasso()
print(cross_val_score(lasso, X, y, cv=5)) ?# 默认是3-fold cross validation################定义一个返回cross-validation rmse error函数来评估模型以便可以选择正确的参数########
from sklearn.linear_model import Ridge, RidgeCV, ElasticNet, LassoCV, LassoLarsCV
from sklearn.model_selection import cross_val_score
?
def rmse_cv(model):
? ? ##使用K折交叉验证模块,将5次的预测准确率打印出
? ? rmse= np.sqrt(-cross_val_score(model, X_train, y_train, scoring="neg_mean_squared_error", cv = 5)) ?#输入训练集的数据和目标值
? ? return(rmse)
? ??
model_ridge = Ridge()
?
alphas = [0.05, 0.1, 0.3, 1, 3, 5, 10, 15, 30, 50, 75]
cv_ridge = [rmse_cv(Ridge(alpha = alpha)).mean() ? ?#对不同的参数alpha,使用岭回归来计算其准确率
? ? ? ? ? ? for alpha in alphas]
?
cv_ridge
?
#绘制岭回归的准确率和参数alpha的变化图
cv_ridge = pd.Series(cv_ridge, index = alphas)
cv_ridge.plot(title = "Validation - Just Do It")
plt.xlabel("alpha")
plt.ylabel("rmse")梯度下降法筛选最优模型
【单个特征】:?x_{cp}xcp?
已知损失函数是?L(w,b)= \sum_{n=1}^{10}\left ( \hat{y}^n - (b + w·x_{cp}) \right )^2L(w,b)=∑n=110?(y^?n?(b+w?xcp?))2?,需要找到一个令结果最小的?f^*f?,在实际的场景中,我们遇到的参数肯定不止?ww,?bb。
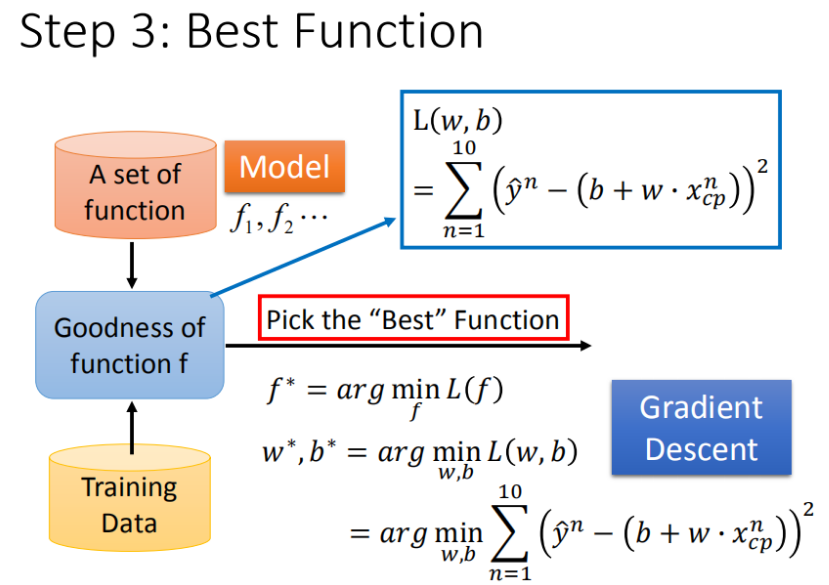
先从最简单的只有一个参数ww入手,定义w^* = arg\ \underset{x}{\operatorname{\min}} L(w)w?=arg?xmin?L(w)

首先在这里引入一个概念 学习率 :移动的步长,如图7中?\etaη
- 步骤1:随机选取一个?w^0w0
- 步骤2:计算微分,也就是当前的斜率,根据斜率来判定移动的方向
- 大于0向右移动(增加ww)
- 小于0向左移动(减少ww)
- 步骤3:根据学习率移动
- 重复步骤2和步骤3,直到找到最低点
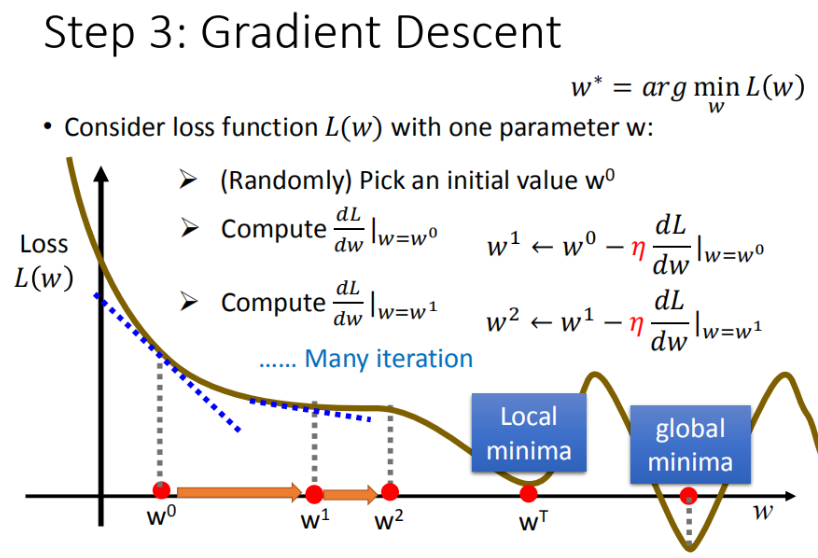
步骤1中,我们随机选取一个?w^0w0,如图8所示,我们有可能会找到当前的最小值,并不是全局的最小值,这里我们保留这个疑问,后面解决。
解释完单个模型参数ww,引入2个模型参数?ww?和?bb?, 其实过程是类似的,需要做的是偏微分,过程如图9所示,偏微分的求解结果文章后面会有解释,详细的求解过程自行Google。

整理成一个更简洁的公式:
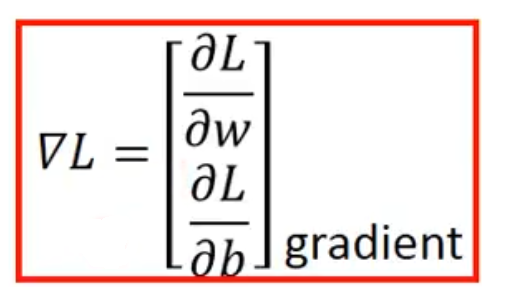
如果把?ww?和?bb?在图形中展示:
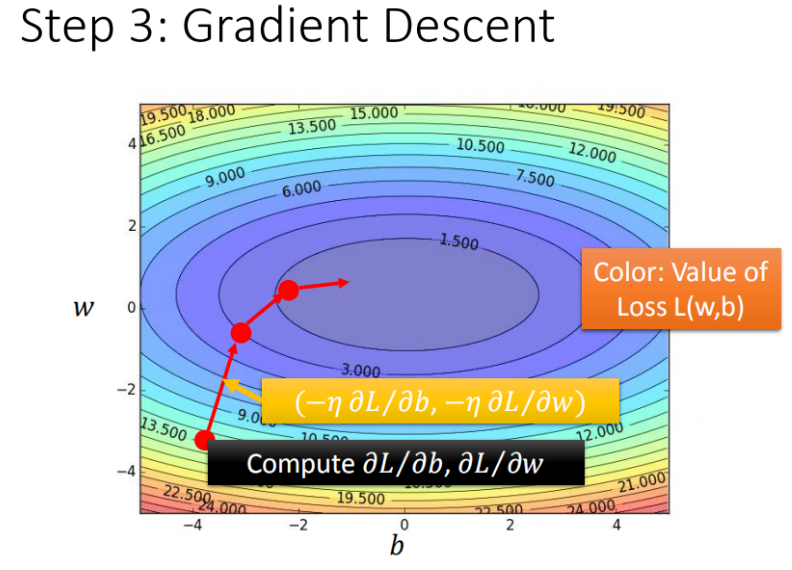
- 每一条线围成的圈就是等高线,代表损失函数的值,颜色约深的区域代表的损失函数越小
- 红色的箭头代表等高线的法线方向
我们通过梯度下降gradient descent不断更新损失函数的结果,这个结果会越来越小,那这种方法找到的结果是否都是正确的呢?前面提到的当前最优问题外,还有没有其他存在的问题呢?

其实还会有其他的问题:
- 问题1:当前最优(Stuck at local minima)
- 问题2:等于0(Stuck at saddle point)
- 问题3:趋近于0(Very slow at the plateau)
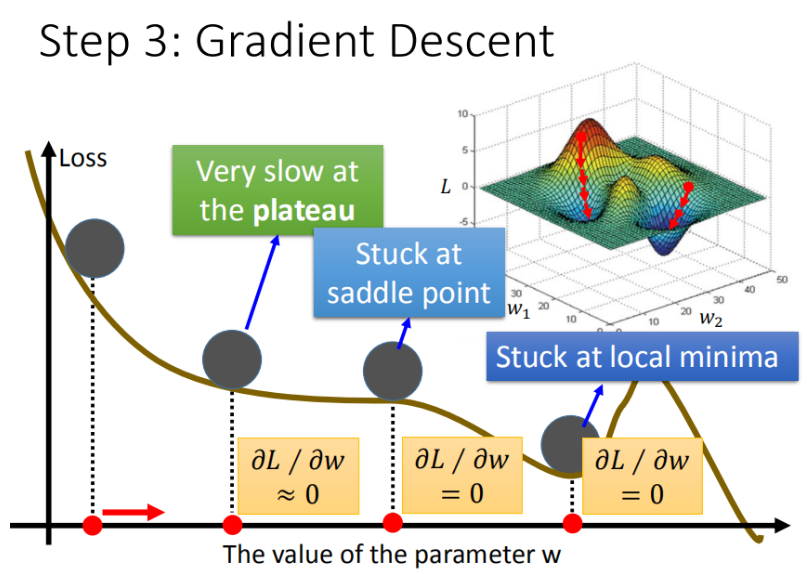
注意:其实在线性模型里面都是一个碗的形状(山谷形状),梯度下降基本上都能找到最优点,但是再其他更复杂的模型里面,就会遇到 问题2 和 问题3 了

?####(注:对b求偏导最后少了一个-1,特此更正)
未完待续,先交作业
Reference
https://blog.csdn.net/weixin_39541558/article/details/80705006