[数据结构与算法]数据结构中的图

基本概念

无向图 & 有向图〔Undirected Graph & Deriected Graph〕

有权图 & 无权图〔Weighted Graph & Unweighted Graph〕

入度 & 出度〔Indegree & Outdegree〕

路径 & 环〔路径：Path〕

有环图〔Cyclic Graph〕

无环图〔Acyclic Graph〕

连通图 & 强连通图

在无向图中，若任意两个顶点 i 与 j 都有路径相通，则称该无向图为连通图。

在有向图中，若任意两个顶点 i 与 j 都有路径相通，则称该有向图为强连通图。

生成树

一个连通图的生成树是指一个连通子图，它含有图中全部 n 个顶点，但只有足以构成一棵树的 n-1 条边。一颗有 n 个顶点的生成树有且仅有 n-1 条边，如果生成树中再添加一条边，则必定成环。在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树，其中代价和指的是所有边的权重和。

图的建立

一般图的题目都不会给你一个现成的图结构。当你知道这是一个图的题目的时候，解题的第一步通常就是建图。这里我简单介绍两种常见的建图方式。

图是有点和边组成的。理论上，我们只要存储图中的所有的边关系即可。

因此我们可以使用数组或者哈希表来存储图，这里我们用二维数组来存储。

• 例题：LeetCode743

class Solution:
    def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
        res=-1
        graph=collections.defaultdict(list)
        for fr,to,w in times:
            graph[fr].append((to,w))
        dist=self.dijkstra(graph, k)
        if len(dist)!=n:
            return -1
        else:
            return max(dist.values())
    def dijkstra(self,graph, start):
        h=[(0,start)]
        dist={}
        while h:
            cost,cur_position=heapq.heappop(h)
            if cur_position in dist.keys():
                continue
            dist[cur_position]=cost
            for v,w in graph[cur_position]:
                if v not in dist.keys():
                    heapq.heappush(h,(cost+w,v))
        return dist

图的遍历

图建立好了，接下来就是要遍历。不管你是什么算法，肯定都要遍历的，一般有以下两种方法（其他奇葩的遍历方式实际意义不大，没有必要学习）。不管是哪一种遍历， 如果图有环，就一定要记录节点的访问情况，防止死循环。当然你可能不需要真正地使用一个集合记录节点的访问情况，比如使用一个数据范围外的数据原地标记，这样的空间复杂度会是 O(1)。

这里以有向图为例， 有向图也是类似，这里不再赘述。

深度优先遍历〔Depth First Search, DFS〕

深度优先遍历图的方法是，从图中某顶点 v 出发， 不断访问邻居， 邻居的邻居直到访问完毕。

广度优先搜索〔Breadth First Search, BFS〕

广度优先搜索，可以被形象地描述为 “浅尝辄止”，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。

需要注意的是 DFS 和 BFS 只是一种算法思想，不是一种具体的算法。 因此其有着很强的适应性，而不是局限于特点的数据结构的，本文讲的图可以用，前面讲的树也可以用。实际上， 只要是非线性的数据结构都可以用。

常见算法

图的题目的算法比较适合套模板。题目类型主要有：

Dijkstra

DIJKSTRA 算法主要解决的是图中任意一点到图中某一个点的最短距离，即单源最短路径。

算法的基本思想是贪心，每次都遍历所有邻居，并从中找到距离最小的，本质上是一种广度优先遍历。这里我们借助堆这种数据结构，使得可以在 logN 的时间内找到 cost 最小的点。

def dijkstra(graph, start, end):
    # 堆里的数据都是 (cost, i) 的二元祖，其含义是“从 start 走到 i 的距离是 cost”。
    heap = [(0, start)]
    visited = set()
    while heap:
        (cost, u) = heapq.heappop(heap)
        if u in visited:
            continue
        visited.add(u)
        if u == end:
            return cost
        for v, c in graph[u]:
            if v in visited:
                continue
            next = cost + c
            heapq.heappush(heap, (next, v))
    return -1

DJ 算法的时间复杂度为 vlogv+e，其中 v 和 e 分别为图中的点和边的个数。

如果是计算一个点到图中所有点的距离呢？我们的算法会有什么样的调整？
拓展例题：Leetcode882

Floyd-Warshall

Floyd-Warshall 也可以解决任意两个点距离，即多源最短路径。Floyd-Warshall 的基本思想是动态规划。该算法的时间复杂度是 $O(N^3)$,空间复杂度是$O(N^2)$，其中 N 为顶点个数。算法也不难理解，简单来说就是： i 到 j 的最短路径 = i 到 k 的最短路径 + k 到 j 的最短路径的最小值。
算法的正确性不言而喻，因为从 i 到 j，要么直接到，要么经过图中的另外一个点 k，中间节点 k 可能有多个，经过中间点的情况取出最小的，自然就是 i 到 j 的最短距离。

# graph 是邻接矩阵，n 是顶点个数
# graph 形如： graph[u][v] = w

def floyd_warshall(graph, n):
    dist = [[float("inf") for _ in range(n)] for _ in range(n)]

    for i in range(n):
        for j in range(n):
            dist[i][j] = graph[i][j]

    # check vertex k against all other vertices (i, j)
    for k in range(n):
        # looping through rows of graph array
        for i in range(n):
            # looping through columns of graph array
            for j in range(n):
                if (
                    dist[i][k] != float("inf")
                    and dist[k][j] != float("inf")
                    and dist[i][k] + dist[k][j] < dist[i][j]
                ):
                    dist[i][j] = dist[i][k] + dist[k][j]
    return dist

例题： LeetCode1462

class Solution(object):
    def checkIfPrerequisite(self, numCourses, prerequisites, queries):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :type queries: List[List[int]]
        :rtype: List[bool]
        """
        graphs=[[False]*numCourses for _ in range(numCourses)]
        for i,j in prerequisites:
            graphs[i][j]=True
        for k in range(numCourses):
            for i in range(numCourses):
                for j in range(numCourses):
                    if not graphs[i][j]:
                        graphs[i][j]=graphs[i][k] and graphs[k][j]
        res=[]
        for i,j in queries:
            if graphs[i][j]:
                res.append(True)
            else:
                res.append(False)
        return res

拓展例题：LeetCode1617. 统计子树中城市之间最大距离

贝尔曼-福特算法

这种解法主要解决单源最短路径，即图中某一点到其他点的最短距离。其基本思想也是动态规划。核心算法为：

• 初始化起点距离为 0

• 对图中的所有边进行若干次处理，直到稳定。处理的依据是：对于每一个有向边 (u,v)，如果 dist[u] + w 小于 dist[v]，那么意味着我们找到了一条到达 v 更近的路，更新之。

• 上面的若干次的上限是顶点 V 的个数，因此不妨直接进行 n 次处理。

• 最后检查一下是否存在负边引起的环。（注意）
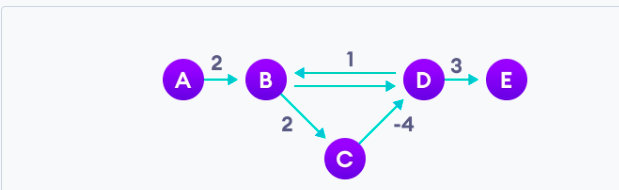
  举个例子。对于如下的一个图，存在一个 B -> C -> D -> B，这样 B 到 C 和 D 的距离理论上可以无限小。我们需要检测到这一种情况，并退出。
  

# Bellman Ford Algorithm in Python


class Graph:

    def __init__(self, vertices):
        self.V = vertices   # Total number of vertices in the graph
        self.graph = []     # Array of edges

    # Add edges
    def add_edge(self, s, d, w):
        self.graph.append([s, d, w])

    # Print the solution
    def print_solution(self, dist):
        print("Vertex Distance from Source")
        for i in range(self.V):
            print("{0}\t\t{1}".format(i, dist[i]))

    def bellman_ford(self, src):

        # Step 1: fill the distance array and predecessor array
        dist = [float("Inf")] * self.V
        # Mark the source vertex
        dist[src] = 0

        # Step 2: relax edges |V| - 1 times
        for _ in range(self.V - 1):#第一次从源开始至少往前进一个节点
            for s, d, w in self.graph:
                if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                    dist[d] = dist[s] + w

        # Step 3: detect negative cycle
        # if value changes then we have a negative cycle in the graph
        # and we cannot find the shortest distances
        for s, d, w in self.graph:
            if dist[s] != float("Inf") and dist[s] + w < dist[d]:
                print("Graph contains negative weight cycle")
                return

        # No negative weight cycle found!
        # Print the distance and predecessor array
        self.print_solution(dist)


g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)

g.bellman_ford(0)

参考阅读：贝尔曼-福特算法
it can work with graphs in which edges can have negative weights.

拓扑排序

在计算机科学领域，有向图的拓扑排序是对其顶点的一种线性排序，使得对于从顶点 u 到顶点 v 的每个有向边 uv， u 在排序中都在之前。当且仅当图中没有定向环时（即有向无环图），才有可能进行拓扑排序。

典型的题目就是给你一堆课程，课程之间有先修关系，让你给出一种可行的学习路径方式，要求先修的课程要先学。任何有向无环图至少有一个拓扑排序。已知有算法可以在线性时间内，构建任何有向无环图的拓扑排序。

Kahn 算法

简单来说，假设 L 是存放结果的列表，先找到那些入度为零的节点，把这些节点放到 L 中，因为这些节点没有任何的父节点。然后把与这些节点相连的边从图中去掉，再寻找图中的入度为零的节点。对于新找到的这些入度为零的节点来说，他们的父节点已经都在 L 中了，所以也可以放入 L。重复上述操作，直到找不到入度为零的节点。如果此时 L 中的元素个数和节点总数相同，说明排序完成；如果 L 中的元素个数和节点总数不同，说明原图中存在环，无法进行拓扑排序。

def topologicalSort(graph):
    """
    Kahn's Algorithm is used to find Topological ordering of Directed Acyclic Graph
    using BFS
    """
    indegree = [0] * len(graph)
    queue = collections.deque()
    topo = []
    cnt = 0

    for key, values in graph.items():
        for i in values:
            indegree[i] += 1#计算每个节点的入度

    for i in range(len(indegree)):
        if indegree[i] == 0:
            queue.append(i)#将入度为0的节点放入queue

    while queue:
        vertex = queue.popleft()
        cnt += 1#计算进入queue的节点个数
        topo.append(vertex)
        for x in graph[vertex]:
            indegree[x] -= 1#入度减1
            if indegree[x] == 0:
                queue.append(x)

    if cnt != len(graph):
        print("Cycle exists")
    else:
        print(topo)
# Adjacency List of Graph
graph = {0: [1, 2], 1: [3], 2: [3], 3: [4, 5], 4: [], 5: []}
topologicalSort(graph)

最小生成树

Kruskal 和 Prim 是两个经典的求最小生成树的算法，本节我们就来了解一下它们。

什么是最小生成树，这两个算法又是如何计算最小生成树的呢？

首先我们来看下什么是生成树。 生成树是一个图的一部分，生成树包含图的所有顶点，且不包含环，这也是为什么叫做生成树，而不是生成图的原因。你可以将生成树看成是根节点不确定的多叉树。

最小生成树是在生成树的基础上加了最小关键字，是最小权重生成树的简称。其指的是对于带权图来说，生成树的权重是其所有边的权重和，那么最小生成树就是权重和最小的生成树，由此可看出，不管是生成树还是最小生成树都可能不唯一。

这在实际生活中有很强的价值。比如我要修建一个地铁，并覆盖 n 个站，如果建造才能使得花费最小？由于每个站之间的路线不同，因此造价也不一样，因此这就是一个最小生成树的实际使用场景，类似的例子还有很多。

Kruskal

Kruskal 算法也被形象地称为加边法，每前进一次都选择权重最小的边，加入到结果集。为了防止环的产生（增加环是无意义的，只要权重是正数，一定会使结果更差），我们需要检查下当前选择的边是否和已经选择的边联通了。如果联通了，是没有必要选取的，因为这会使得环产生。因此算法上，我们可使用并查集辅助完成。下面算法中的 find_parent 部分，实际上就是并查集的核心代码，只是我们没有将其封装并使用罢了。

Kruskal 具体算法：

• 对边进行排序

• 将 n 个顶点初始化为 n 个联通域

• 按照权值从小到大选择边加入到结果集，如果当前选择的边和已经选择的边联通了，则放弃选择，否则进行选择，加入到结果集。

• 重复 3 直到我们找到了一个联通域大小为 n 的子图

from typing import List, Tuple
def kruskal(num_nodes: int, edges: List[Tuple[int, int, int]]) -> int:
 """
    >>> kruskal(4, [(0, 1, 3), (1, 2, 5), (2, 3, 1)])
    [(2, 3, 1), (0, 1, 3), (1, 2, 5)]
    """
    edges=sorted(edges,key=lambda x: x[-1])#对边进行排序
    parent=range(num_nodes)#将 n 个顶点初始化为 n 个联通域
    def find_parent(i):
    	if i!=parent[i]:
    		parent[i]=find_parent(parent[i])
    	return parent[i]
    minimum_spanning_tree_cost = 0
    minimum_spanning_tree = []
    for a,b,w in edges:#构建并查集
    	if find_parent(a)!=find_parent(b):#a和b不在同一个连通域
    		minimum_spanning_tree.append((a,b,w))
    		minimum_spanning_tree_cost+=w
    		parent[a]=b#加入到结果集，将a和b放入一个连通域
    

Prim

Prim 算法也被形象地称为加点法，每前进一次都选择权重最小的点，加入到结果集。形象地看就像一个不断生长的真实世界的树。

Prim 具体算法：

• 初始化最小生成树点集 MV 为图中任意一个顶点，最小生成树边集 ME 为空。我们的目标是将 MV 填充到 和 V 一样，而边集则根据 MV 的产生自动计算。

• 在集合 E 中 （集合 E 为原始图的边集）选取最小的边 <u, v> 其中 u 为 MV 中已有的元素，而 v 为 MV 中不存在的元素（像不像上面说的不断生长的真实世界的树），将 v 加入到 MV，将 <u, v> 加到 ME。

• 重复 2上述步骤直到我们找到了一个联通域大小为 n 的子图

import sys
from collections import defaultdict
def PrimsAlgorithm(l): 
    nodePosition = []
    def get_position(vertex):
        return nodePosition[vertex]
    def set_position(vertex, pos):
        nodePosition[vertex] = pos
    def top_to_bottom(heap, start, size, positions):
        if start > size // 2 - 1:
            return
        else:
            if 2 * start + 2 >= size:
                m = 2 * start + 1
            else:
                if heap[2 * start + 1] < heap[2 * start + 2]:
                    m = 2 * start + 1
                else:
                    m = 2 * start + 2
            if heap[m] < heap[start]:
                temp, temp1 = heap[m], positions[m]
                heap[m], positions[m] = heap[start], positions[start]
                heap[start], positions[start] = temp, temp1

                temp = get_position(positions[m])
                set_position(positions[m], get_position(positions[start]))
                set_position(positions[start], temp)

                top_to_bottom(heap, m, size, positions)

    # Update function if value of any node in min-heap decreases
    def bottom_to_top(val, index, heap, position):
        temp = position[index]

        while index != 0:
            if index % 2 == 0:
                parent = int((index - 2) / 2)
            else:
                parent = int((index - 1) / 2)

            if val < heap[parent]:
                heap[index] = heap[parent]
                position[index] = position[parent]
                set_position(position[parent], index)
            else:
                heap[index] = val
                position[index] = temp
                set_position(temp, index)
                break
            index = parent
        else:
            heap[0] = val
            position[0] = temp
            set_position(temp, 0)

    def heapify(heap, positions):
        start = len(heap) // 2 - 1
        for i in range(start, -1, -1):
            top_to_bottom(heap, i, len(heap), positions)

    def deleteMinimum(heap, positions):
        temp = positions[0]
        heap[0] = sys.maxsize
        top_to_bottom(heap, 0, len(heap), positions)
        return temp

    visited = [0 for i in range(len(l))]
    Nbr_TV = [-1 for i in range(len(l))]  # Neighboring Tree Vertex of selected vertex
    # Minimum Distance of explored vertex with neighboring vertex of partial tree
    # formed in graph
    Distance_TV = []  # Heap of Distance of vertices from their neighboring vertex
    Positions = []

    for x in range(len(l)):
        p = sys.maxsize
        Distance_TV.append(p)
        Positions.append(x)
        nodePosition.append(x)

    TreeEdges = []
    visited[0] = 1
    Distance_TV[0] = sys.maxsize
    for x in l[0]:
        Nbr_TV[x[0]] = 0
        Distance_TV[x[0]] = x[1]
    heapify(Distance_TV, Positions)

    for i in range(1, len(l)):
        vertex = deleteMinimum(Distance_TV, Positions)
        if visited[vertex] == 0:
            TreeEdges.append((Nbr_TV[vertex], vertex))
            visited[vertex] = 1
            for v in l[vertex]:
                if visited[v[0]] == 0 and v[1] < Distance_TV[get_position(v[0])]:
                    Distance_TV[get_position(v[0])] = v[1]
                    bottom_to_top(v[1], get_position(v[0]), Distance_TV, Positions)
                    Nbr_TV[v[0]] = vertex
    return TreeEdges


if __name__ == "__main__":  # pragma: no cover
    # < --------- Prims Algorithm --------- >
    n = int(input("Enter number of vertices: ").strip())
    e = int(input("Enter number of edges: ").strip())
    adjlist = defaultdict(list)
    for x in range(e):
        l = [int(x) for x in input().strip().split()]  # noqa: E741
        adjlist[l[0]].append([l[1], l[2]])
        adjlist[l[1]].append([l[0], l[2]])
    print(PrimsAlgorithm(adjlist))

两种算法比较

为了后面描述方便，我们令 V 为图中的顶点数， E 为图中的边数。那么 KruKal 的算法复杂度是 O(ElogE)O(ElogE)，Prim 的算法时间复杂度为 E + VlogVE+VlogV。

KruKal 是基于图的联通性贪心算法。而 Prim 则是基于堆的贪心算法。

A 星寻路算法

A 星寻路解决的问题是在一个二维的表格中找出任意两点的最短距离或者最短路径。常用于游戏中的 NPC 的移动计算，是一种常用启发式算法。一般这种题目都会有障碍物。除了障碍物，力扣的题目还会增加一些限制，使得题目难度增加。

这种题目一般都是力扣的困难难度。理解起来不难， 但是要完整地没有 bug 地写出来却不那么容易。

在该算法中，我们从起点开始，检查其相邻的四个方格并尝试扩展，直至找到目标。A 星寻路算法的寻路方式不止一种，感兴趣的可以自行了解一下。

公式表示为： f(n)=g(n)+h(n)。

其中：

f(n) 是从初始状态经由状态 n 到目标状态的估计代价，

g(n) 是在状态空间中从初始状态到状态 n 的实际代价，

h(n) 是从状态 n 到目标状态的最佳路径的估计代价。

如果 g(n)为 0，即只计算任意顶点 n 到目标的评估函数 h(n)，而不计算起点到顶点 n 的距离，则算法转化为使用贪心策略的最良优先搜索，速度最快，但可能得不出最优解； 如果 h(n)不大于顶点 n 到目标顶点的实际距离，则一定可以求出最优解，而且 h(n)越小，需要计算的节点越多，算法效率越低，常见的评估函数有——欧几里得距离、曼哈顿距离、切比雪夫距离； 如果 h(n)为 0，即只需求出起点到任意顶点 n 的最短路径 g(n)，而不计算任何评估函数 h(n)，则转化为单源最短路径问题，即 Dijkstra 算法，此时需要计算最多的顶点；

这里有一个重要的概念是估价算法，一般我们使用曼哈顿距离来进行估价。

grid = [
    [0, 1, 0, 0, 0, 0],
    [0, 1, 0, 0, 0, 0],  # 0 are free path whereas 1's are obstacles
    [0, 1, 0, 0, 0, 0],
    [0, 1, 0, 0, 1, 0],
    [0, 0, 0, 0, 1, 0],
]

"""
heuristic = [[9, 8, 7, 6, 5, 4],
             [8, 7, 6, 5, 4, 3],
             [7, 6, 5, 4, 3, 2],
             [6, 5, 4, 3, 2, 1],
             [5, 4, 3, 2, 1, 0]]"""

init = [0, 0]
goal = [len(grid) - 1, len(grid[0]) - 1]  # all coordinates are given in format [y,x]
cost = 1

# the cost map which pushes the path closer to the goal
heuristic = [[0 for row in range(len(grid[0]))] for col in range(len(grid))]
for i in range(len(grid)):
    for j in range(len(grid[0])):
        heuristic[i][j] = abs(i - goal[0]) + abs(j - goal[1])
        if grid[i][j] == 1:
            heuristic[i][j] = 99  # added extra penalty in the heuristic map


# the actions we can take
delta = [[-1, 0], [0, -1], [1, 0], [0, 1]]  # go up  # go left  # go down  # go right


# function to search the path
def search(grid, init, goal, cost, heuristic):
    closed = [
        [0 for col in range(len(grid[0]))] for row in range(len(grid))
    ]  # the reference grid
    closed[init[0]][init[1]] = 1
    action = [
        [0 for col in range(len(grid[0]))] for row in range(len(grid))
    ]  # the action grid

    x = init[0]
    y = init[1]
    g = 0
    f = g + heuristic[init[0]][init[0]]
    cell = [[f, g, x, y]]

    found = False  # flag that is set when search is complete
    resign = False  # flag set if we can't find expand

    while not found and not resign:#优先搜索
        if len(cell) == 0:
            return "FAIL"
        else:  # to choose the least costliest action so as to move closer to the goal
            cell.sort()
            cell.reverse()
            next = cell.pop()
            x = next[2]
            y = next[3]
            g = next[1]

            if x == goal[0] and y == goal[1]:
                found = True
            else:
                for i in range(len(delta)):  # to try out different valid actions
                    x2 = x + delta[i][0]
                    y2 = y + delta[i][1]
                    if x2 >= 0 and x2 < len(grid) and y2 >= 0 and y2 < len(grid[0]):
                        if closed[x2][y2] == 0 and grid[x2][y2] == 0:
                            g2 = g + cost
                            f2 = g2 + heuristic[x2][y2]
                            cell.append([f2, g2, x2, y2])
                            closed[x2][y2] = 1
                            action[x2][y2] = i##关键点：记录action数组，方便回溯
    invpath = []
    x = goal[0]
    y = goal[1]
    invpath.append([x, y])  # we get the reverse path from here
    while x != init[0] or y != init[1]:
        x2 = x - delta[action[x][y]][0]
        y2 = y - delta[action[x][y]][1]
        x = x2
        y = y2
        invpath.append([x, y])

    path = []
    for i in range(len(invpath)):
        path.append(invpath[len(invpath) - 1 - i])
    print("ACTION MAP")
    for i in range(len(action)):
        print(action[i])
    return path


a = search(grid, init, goal, cost, heuristic)
for i in range(len(a)):
    print(a[i])

例题：LeetCode1263推箱子

二分图

着色法
Leetcode886
给定一组 N 人（编号为 1, 2, …, N）， 我们想把每个人分进任意大小的两组。

每个人都可能不喜欢其他人，那么他们不应该属于同一组。

形式上，如果 dislikes[i] = [a, b]，表示不允许将编号为 a 和 b 的人归入同一组。

当可以用这种方法将每个人分进两组时，返回 true；否则返回 false。

示例 1：

输入：N = 4, dislikes = [[1,2],[1,3],[2,4]]
输出：true
解释：group1 [1,4], group2 [2,3]
示例 2：

输入：N = 3, dislikes = [[1,2],[1,3],[2,3]]
输出：false
示例 3：

输入：N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
输出：false

提示：

1 <= N <= 2000
0 <= dislikes.length <= 10000
dislikes[i].length == 2
1 <= dislikes[i][j] <= N
dislikes[i][0] < dislikes[i][1]
对于dislikes[i] == dislikes[j] 不存在 i != j

#解答
class Solution:
    def possibleBipartition(self, n: int, dislikes: List[List[int]]) -> bool:
        dislikes_mat=[[0]*n for _ in range(n)]
        for fr,to in dislikes:
            dislikes_mat[fr-1][to-1]=1
            dislikes_mat[to-1][fr-1]=1
        partition=[0]*n
        for i in range(n):
            if partition[i]==0 and not self.dfs(dislikes_mat,n,partition,i,1):
                return False
        return True
    def dfs(self,dislikes_mat,n,partition,i,color):
        partition[i]=color#重点！！
        for index,j in enumerate(dislikes_mat[i]):
            if j==1:#index>i不需要这个条件
                if partition[index]==color:
                    return False
                if partition[index]==0 and not self.dfs(dislikes_mat,n,partition,index,-1*color):
                    return False
        return True

LeetCode785
着色法
给定一个无向图 graph，当这个图为二分图时返回 true。

如果我们能将一个图的节点集合分割成两个独立的子集 A 和 B，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，我们就将这个图称为二分图。

graph 将会以邻接表方式给出，graph[i]表示图中与节点 i 相连的所有节点。每个节点都是一个在 0 到 graph.length-1 之间的整数。这图中没有自环和平行边： graph[i] 中不存在 i，并且 graph[i]中没有重复的值。

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        n=len(graph)
        graph_mat=[[0]*n for _ in range(n)]
        for i,g in enumerate(graph):
            if g:
                for j in g:
                    graph_mat[i][j]=1
                    graph_mat[j][i]=1
        colors=[0]*n
        for i in range(n):
            if colors[i]==0 and not self.dfs(graph_mat,n,i,colors,1):
                return False
        return True
    def dfs(self,graph_mat,n,i,colors,color):
        colors[i]=color
        for j in range(n):
            if graph_mat[i][j]==1:
                if colors[j]==color:
                    return False
                if colors[j]==0 and not self.dfs(graph_mat,n,j,colors,-1*color):
                    return False
        return True         

并查集

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        n=len(graph)
        parent=list(range(n))#初始化
        def find_parent(i):#构建并查集
            if i!=parent[i]:
                parent[i]=find_parent(parent[i])
            return parent[i]
        for i,g in enumerate(graph):
            if g:
                for j in g:
                    if find_parent(i)==find_parent(j):
                        return False
                    parent[j]=find_parent(g[0])
        return True

更多做法：

class UF:
    def __init__(self, n):
        self.parent = {}
        for i in range(n):
            self.parent[i] = i
    def union(self, i,j):
        self.parent[self.find(i)] = self.find(j)
    def find(self, i):
        if i == self.parent[i]: return i
        self.parent[i] = self.find(self.parent[i])
        return self.parent[i]
    def is_connected(self, i,j):
        return self.find(i) == self.find(j)

class Solution:
    def isBipartite(self, graph: List[List[int]]) -> bool:
        n = len(graph)
        uf = UF(n)
        for i in range(n):
            for neibor in graph[i]:
                if uf.is_connected(i, neibor): return False
                uf.union(graph[i][0], neibor)
        return True

总结

理解图的常见概念，我们就算入门了。接下来，我们就可以做题了，一般的图题目第一步都是建图，第二步都是基于第一步的图进行遍历以寻找可行解。