题目来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems
特别鸣谢:来自夸夸群的 醉笑陪公看落花@知乎,王不懂不懂@知乎
感谢醉笑陪公看落花@知乎 倾囊相授,感谢小伙伴们督促学习,一起进步
可以用字符串表示一个学生的出勤记录,其中的每个字符用来标记当天的出勤情况(缺勤、迟到、到场)。记录中只含下面三种字符:
‘A’:Absent,缺勤
‘L’:Late,迟到
‘P’:Present,到场
如果学生能够 同时 满足下面两个条件,则可以获得出勤奖励:
按 总出勤 计,学生缺勤(‘A’)严格 少于两天。
学生 不会 存在 连续 3 天或 连续 3 天以上的迟到(‘L’)记录。
给你一个整数 n ,表示出勤记录的长度(次数)。请你返回记录长度为 n 时,可能获得出勤奖励的记录情况 数量 。答案可能很大,所以返回对 109 + 7 取余 的结果。
示例 1:
输入:n = 2
输出:8
解释:
有 8 种长度为 2 的记录将被视为可奖励:
“PP” , “AP”, “PA”, “LP”, “PL”, “AL”, “LA”, “LL”
只有"AA"不会被视为可奖励,因为缺勤次数为 2 次(需要少于 2 次)。
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/student-attendance-record-ii
深度优先-DFS - 超时
由于字符串的每个位置有三种情况,可以考虑使用深度优先遍历,每一次有三个选择 ,类似于 leetcode 576. 出界的路径数-DFS-库函数-动态规划 文章在网格中有四种方向可以选择
时间复杂度是n! 超时了
class Solution:
def checkRecord(self, n: int) -> int:
import functools
@functools.lru_cache(None)
def DFS(i,ca,cl):
if ca == 2:return 0
if cl == 3:return 0
if i == n :return 1
return sum(
[DFS(i+1,ca+1,0)%(pow(10,9)+7),
DFS(i+1,ca,cl+1)%(pow(10,9)+7),
DFS(i+1,ca,0)%(pow(10,9)+7)]
)%(pow(10,9)+7)
return DFS(0,0,0)
动态规划 dp - 通过
定义安全状态,第i天有如下7种情况
A 第i天缺席
L with L0 with A0 第i天迟到,在0次缺席,前一天未迟到的情况下
L with L1 with A0 第i天迟到,在0次缺席,前一天迟到的情况下
L with L0 with A1 第i天迟到,在1次缺席,前一天未迟到的情况下
L with L1 with A1 第i天迟到,在1次缺席,前一天迟到的情况下
P with A0 第i天出席,在0次缺席的情况下
P with A1 第i天出席,在1次缺席的情况下
最后求第n天的所有情况之和即可
class Solution:
def checkRecord(self, n: int) -> int:
dp = [[0]*7 for _ in range(n)]
dpi_1 = [1,1,0,0,0,1,0] # 第 0天
for i in range(1,n): # 第 i天
dpi = [sum([dpi_1[j] for j in [1,2,5]])%(pow(10,9)+7),
dpi_1[5],
dpi_1[1],
sum([dpi_1[j] for j in [0,6]])%(pow(10,9)+7),
dpi_1[3],
sum([dpi_1[j] for j in [1,2,5]])%(pow(10,9)+7),
sum([dpi_1[j] for j in [0,3,4,6]])%(pow(10,9)+7)]
dpi_1 = dpi[:]
return sum(dpi_1)%(pow(10,9)+7)
执行情况
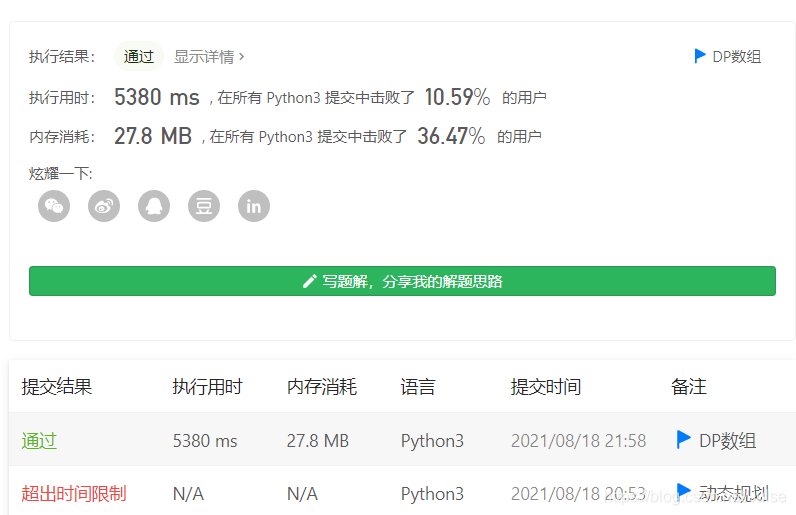
其他解决方法
官方解题方法:
https://leetcode-cn.com/problems/student-attendance-record-ii/solution/xue-sheng-chu-qin-ji-lu-ii-by-leetcode-s-kdlm/
收获
- 压缩动态规划状态 dp[i][j] = dp[i*n+j]
- 转移函数写成矩阵形式
- 用快速幂求矩阵的n次方,把时间复杂度从O(n) 降低到O(log2(n))
官方-方法1- dp
class Solution:
def checkRecord(self, n: int) -> int:
MOD = 10**9 + 7
# A 的数量,结尾连续 L 的数量
dp = [[0, 0, 0], [0, 0, 0]]
dp[0][0] = 1
for i in range(1, n + 1):
dpNew = [[0, 0, 0], [0, 0, 0]]
# 以 P 结尾的数量
for j in range(0, 2):
for k in range(0, 3):
dpNew[j][0] = (dpNew[j][0] + dp[j][k]) % MOD
# 以 A 结尾的数量
for k in range(0, 3):
dpNew[1][0] = (dpNew[1][0] + dp[0][k]) % MOD
# 以 L 结尾的数量
for j in range(0, 2):
for k in range(1, 3):
dpNew[j][k] = (dpNew[j][k] + dp[j][k - 1]) % MOD
dp = dpNew
total = 0
for j in range(0, 2):
for k in range(0, 3):
total += dp[j][k]
return total % MOD
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/student-attendance-record-ii/solution/xue-sheng-chu-qin-ji-lu-ii-by-leetcode-s-kdlm/
官方-dp-矩阵快速幂
如果遇到i状态只和i-1状态相关,那是不是都可以用矩阵快速幂来降低时间复杂度呢?

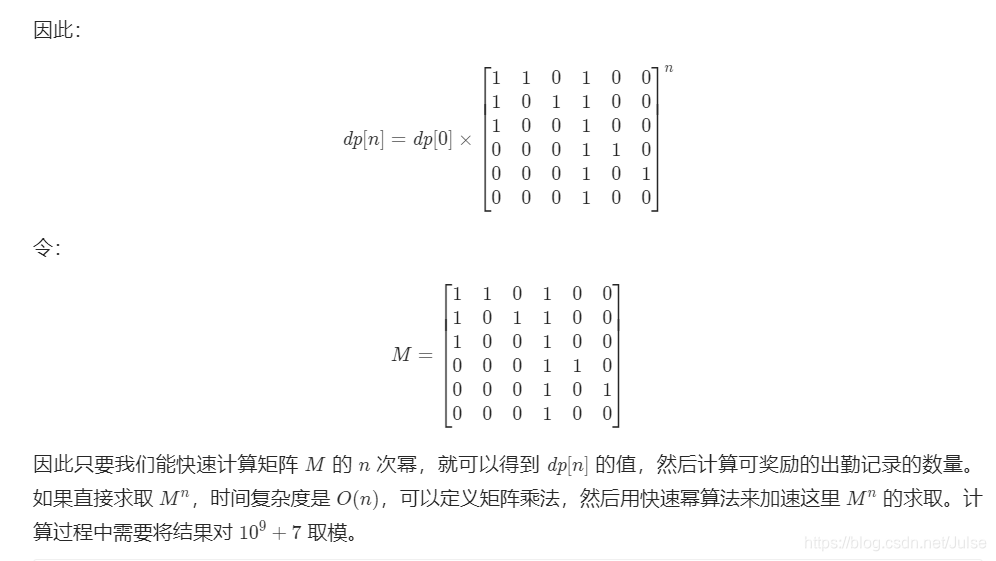
class Solution:
def checkRecord(self, n: int) -> int:
MOD = 10**9 + 7
mat = [
[1, 1, 0, 1, 0, 0],
[1, 0, 1, 1, 0, 0],
[1, 0, 0, 1, 0, 0],
[0, 0, 0, 1, 1, 0],
[0, 0, 0, 1, 0, 1],
[0, 0, 0, 1, 0, 0],
]
def multiply(a: List[List[int]], b: List[List[int]]) -> List[List[int]]:
rows, columns, temp = len(a), len(b[0]), len(b)
c = [[0] * columns for _ in range(rows)]
for i in range(rows):
for j in range(columns):
for k in range(temp):
c[i][j] += a[i][k] * b[k][j]
c[i][j] %= MOD
return c
def matrixPow(mat: List[List[int]], n: int) -> List[List[int]]:
ret = [[1, 0, 0, 0, 0, 0]]
while n > 0:
if (n & 1) == 1:
ret = multiply(ret, mat)
n >>= 1
mat = multiply(mat, mat)
return ret
res = matrixPow(mat, n)
ans = sum(res[0])
return ans % MOD
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/student-attendance-record-ii/solution/xue-sheng-chu-qin-ji-lu-ii-by-leetcode-s-kdlm/