[数据结构与算法]逻辑回归实现

有监督学习–逻辑回归

一:算法原理

区别于线性回归,逻辑回归输出的是分类变量

作用:基于线性回归的原理,解决二分类问题或者多分类问题

1.Sigmoid函数:例如:对数几率函数

2.公式

$$\begin{gathered} 逻辑回归表达式:y=\frac{1}{1+e^{?(W^{T}x+b)}} \\ 进一步可得:ln\frac{y}{1?y}=W^{T}x+b \\ 举例如下: \\ 二分类:1的概率P,则0的概率1?P \\ ln\frac{P}{1?P}=W^{T}x+b \\ 所以ln\frac{P}{1?P}又称为对数几率,反映了样本取正例1的相对可能性 \end{gathered}$$

二:梯度下降

线性回归通过最小二乘法得到最小的损失函数

逻辑回归通过梯度下降得到最小得损失函数

三:sklean实现逻辑回归

#1.导入数据--乳腺癌数据
import pandas as pd 
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
X = load_breast_cancer().data
Y = load_breast_cancer().target

#2.建模
from sklearn.linear_model import LogisticRegression as LR
from sklearn.model_selection import train_test_split

#3.实例化
lr2 = LR(penalty='l2',solver='liblinear',C=0.5,max_iter=1000).fit(X,Y)
lr1 = LR(penalty='l1',solver='liblinear',C=0.5,max_iter=1000).fit(X,Y)

score1 = lr1.score(X,Y)
score2 = lr2.score(X,Y)
print(score1)
print(score2)

#4.查看w参数值
lr1.coef_     #通过参数输出结果可以看出参数少了很多,所以通过penalty='l1'的建模方式可以进行特征筛选,可以防止过拟合
lr2.coef_     #通过参数输出结果可以看出penalty='l2'的建模方式会更加复杂,因为不能进行特征筛选,容易过拟合

#5.查看每一行分类预测的结果概率值
#结果中每一行有两个概率值,第一个代表预测是0的概率,第二个代表预测为1的概率,两者相加=1
lr1.predict_proba(X) 
lr2.predict_proba(X)

逻辑回归模型参数描述:

# 参数描述
# LR(
#     penalty='l2',  #l2->岭回归 , l1->lasso  两种正则化方式,目的是防止过拟合
#     dual=False,
#     tol=0.0001,
#     C=1.0,       #C值越小,表示惩罚力度越大,反之亦然,
#     fit_intercept=True,
#     intercept_scaling=1,
#     class_weight=None,
#     random_state=None,
#     solver='lbfgs',   #梯度下降的方式,4种可选的算法 ('newton-cg','Ibfgs','liblinear','sag'} 
#     max_iter=100,     #梯度下降的最大迭代次数
#     multi_class='auto',
#     verbose=0,
#     warm_start=False,
#     n_jobs=None,
#     l1_ratio=None,
# )

l1 和 l2 两种正则化对比模型的参数个数:

l1:可以进行特征筛选,可以防止过拟合

l2:不能进行特征筛选,模型复杂度更高,容易过拟合

四:绘制学习曲线,对比不同参数的效果

4.1 绘制C值的学习曲线,C值越小则惩罚力度越大,反之亦然

#绘制学习曲线
#1.切割数据集
Xtrain,Xtest,Ytrain,Ytest = train_test_split(X,Y,test_size=0.3,random_state=420)

#2.目的:对比 l1 和 l2 在不同C值之间的表现
l1_train=[]
l2_train=[]
l1_test=[]
l2_test=[]

for i in np.linspace(0.05,1,19):  #代表在0.05 和 1 之间取20个数据
    #实例化同时进行训练
    lr1 = LR(penalty='l1',C=i,solver='liblinear',max_iter=1000).fit(Xtrain,Ytrain)
    lr2 = LR(penalty='l2',C=i,solver='liblinear',max_iter=1000).fit(Xtrain,Ytrain)

    #记录每次不同C值得得分
    l1_train.append(lr1.score(Xtrain,Ytrain)) #训练集的分数
    l2_train.append(lr2.score(Xtrain,Ytrain)) #训练集的分数
    l1_test.append(lr1.score(Xtest,Ytest)) #测试集的分数
    l2_test.append(lr2.score(Xtest,Ytest)) #测试集的分数
    
    
#2.画图
graph = [l1_train,l2_train,l1_test,l2_test]
color=['red','green','blue','black']
label=['l1_train','l2_train','l1_test','l2_test']

plt.figure(figsize=(6.,6))

for i in range(len(graph)): #循环多条线
    plt.plot(np.linspace(0.05,1,19),graph[i],color=color[i],label=label[i])

plt.legend(loc=4)
plt.show()
     

4.2 在C值确定=0.9的前提下去绘制梯度下降的最大迭代次数max_iter 的学习曲线

#当C=0.9,绘制最大迭代次数学习曲线
l1_train=[]
l1_test=[]

for i in range(1,201,10):  #代表在0.05 和 1 之间取20个数据
    #实例化同时进行训练
    lr1 = LR(penalty='l1',C=0.9,solver='liblinear',max_iter=i).fit(Xtrain,Ytrain)

    #记录每次不同C值得得分
    l1_train.append(lr1.score(Xtrain,Ytrain)) #训练集的分数
    l1_test.append(lr1.score(Xtest,Ytest)) #测试集的分数

#2.画图
plt.plot(range(1,201,10),l1_train,color='red',label='l1_train')
plt.plot(range(1,201,10),l1_test,color='green',label='l1_test')
plt.legend(loc=4)
plt.show()

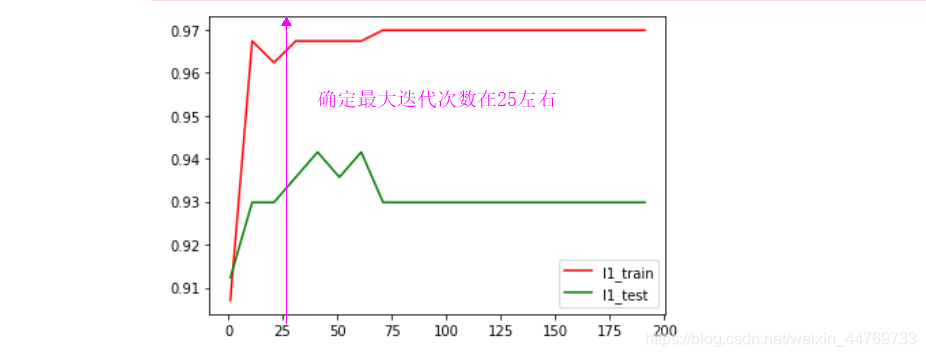
4.3 在确定C=0.9 , max_iter =25 的前提下绘制不同梯度下降的方法的学习曲线

solver 的四种取值: (‘newton-cg’,‘Ibfgs’,‘liblinear’,‘sag’)

• liblinear∶使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。
• Ibfgs∶拟牛顿法的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。
• newton-cg∶也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函
  数。
• sag∶即随机平均梯度下降，是梯度下降法的变种，和普通梯度下降法的区别是每次迭代仅用一部
  分的样本来计算梯度，适合于样本数据多的时候。

注意:

1.Ibfgs / newton-cg / sag 这三种梯度下降的方法前提条件是 损失函数必须是可导的

2.同时这三种可导的方式不可以使用于 penalty=‘l1’ 的范式

五:网格搜索–确定最优参数

一步解决所有参数的最优解: C / max_iter / solver

#网格搜索
from sklearn.model_selection import GridSearchCV #网格搜素
from sklearn.preprocessing import StandardScaler #标准化,消除数据量纲的影响

#1.把数据放进DataFrame
data = pd.DataFrame(X,columns=load_breast_cancer().feature_names)
data['label']=Y
data.head()

#2.切分数据集
Xtrain,Xtest,Ytrain,Ytest = train_test_split(data.iloc[:,:-1],data.iloc[:,-1],test_size=0.3,random_state=420)
#3.对数据集进行标准化
std = StandardScaler().fit(Xtrain)
Xtrain_std = std.transform(Xtrain)
Xtest_std = std.transform(Xtest)

#3.进行网格搜索,确定哪种算法和参数是最优的
#在l2范式下进行测试
params = {
     'C':list(np.linspace(0.05,1,19)),
    'solver':['newton-cg','Ibfgs','liblinear','sag']
}
model = LR(penalty='l2',max_iter=1000)
gs = GridSearchCV(model,params,cv=5)
gs.fit(Xtrain_std,Ytrain) #使用标准化之后的数据集 Xtrain_std

#4.查看最优的参数
gs.best_score_  #最高分数:0.9874683544303797
gs.best_params_ #最优参数结果:{'C': 0.3138888888888889, 'solver': 'newton-cg'}

#5.将最优参数 {'C': 0.3138888888888889, 'solver': 'newton-cg'} 代入模型,对比训练集和测试集的结果
lr3 = LR(penalty='l2',max_iter=1000,C=gs.best_params_['C'],solver=gs.best_params_['solver']).fit(Xtrain_std,Ytrain)
train_score = lr3.score(Xtrain_std,Ytrain)
test_score = lr3.score(Xtest_std,Ytest)
print('最优参数下的训练集得分=',train_score,'最优参数下的测试集得分=',test_score)
#结果: 最优参数下的训练集得分= 0.9874371859296482 最优参数下的测试集得分= 0.9649122807017544