[数据结构与算法]删除并获得点数（动态规划）

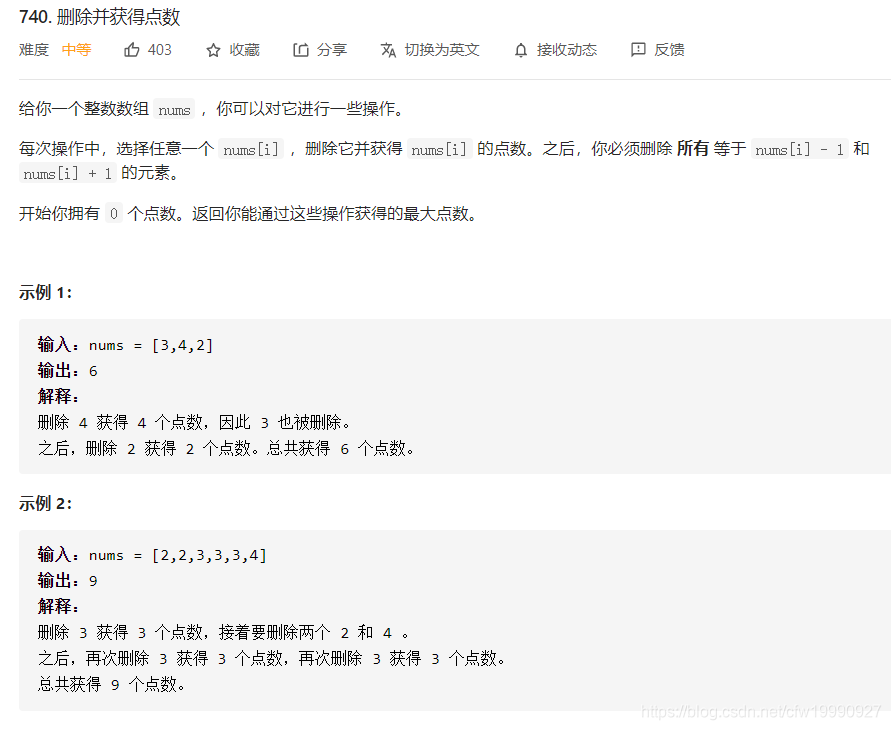
题目解析：

1.随机选择一个数nums[i],并将其删除，获得nums[i]的点数，之后删除掉所有的数nums[n+1]和nums[n-1]

        例如示例二中，我们随机选择删除数2，并获得其点数，那么将会删除数组中所有的1和3 。
        此时，数组中还有【2，4】,我们可以再次选择删除数2，并获得其点数。
        
   最终我们可以发现如果选择了数n,那么就会获得所有数n的点数

虽然分析了题目，但是还是没有看出nums数组可以递推的趋势，不妨将数组nums转变一下？

我们可以将数组nums中值相同的数的和记录到一个数组sum中，例如【2，2，2，2，3，3】可以转换为【0，0，8，6】
具体转变的方法： 将下标Index当作数值，sum[Index]当作每个值的总和，数组nums中有4个2，那么sum[2]=2*4;有2个3，那么sum[3]=2*3;

将【2，2，3，3，3，4】转变成【0，0，4，9，4】

此时就可以将问题转变为sum数组中，可以随机选择nums[i]，一旦选择了nums[i],那么nums[i-1]和nums[i+1]都不能选择，求可以选择出数的最大总和？(动态规划思想直观的体现)

代码展示

class Solution {
    public static int[] change(int[] nums)//change函数是将nums数组转换为sum数组
    {
        int Maxs=0;
       for(int value:nums)           //寻找出nums数组中最大的数值
         Maxs=Math.max(Maxs,value); 
        
       int[] sum=new int[Maxs+1];
        for(int value:nums)        //将nums数组中相同数值的总和存储在sum数值中
            sum[value]+=value;     //sum数值中的下标代表nums中的数值
       return sum;                 //sum[i]就是nums中数值为i的数的总和
    }
    public int deleteAndEarn(int[] nums) {
        int[] sum=change(nums);
        if(sum.length==0)
            return 0;
        else if(sum.length==1)
            return sum[0];
        else if(sum.length==2)
            return Math.max(sum[0],sum[1]);
        int a=sum[0],b=Math.max(sum[0],sum[1]);
        int c=0;
        for(int i=2;i<sum.length;i++)     //滑动数组
        {                                 //递推的关系是dp[i]=Math.max(dp[i-1],dp[i-2]+sum[i])
            c=Math.max(a+sum[i],b);
            a=b;
            b=c;
        }
        return c;
    }
}