一、基本概念
逻辑回归:将回归转化成为二分类,并能得出概率值
应用场景:广告点击率、是否为垃圾邮件、是否是金融诈骗
问题:如何将回归转换成为分类
解答:使用sigmoid 函数,将输入的数据转化成为一个[0,1]之间的数值,即概率值
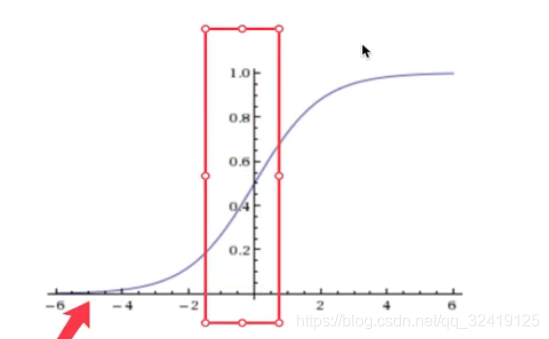
具体体现在下图的逻辑回归公式图中。其中,z表示回归的结果,e=2.71,g(z)为sigmoid函数。

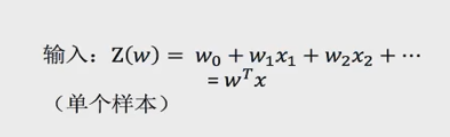
由此可知,逻辑回归和线性回归一样,都是输入数据,拟合参数。不同点在于逻辑回归用sigmoid函数将z值转化成了一个[0,1]之间的数值,默认阈值为0.5,由此变成了二分类问题。
二、参数优化
逻辑回归是线性回归,线性回归的存在最优参数,即使均方误差最小的参数。寻找最优参数的方法为,正式方程或网格搜索。而逻辑回归通过对数似然损失来找最优参数。
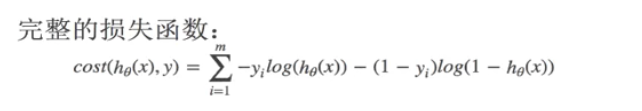
均方误差不存在多个局部最低点,全局只有一个最小值。而对数似然损失存在多个局部最低点。由于目前还是无法找到全局最低点,因此只能通过下列方法尽量解决:1.多次随机初始化,找出几个局部最低点并进行比较;2.求解过程中,调整学习率,使模型学习地慢一些。
尽管对数似然损失函数没有全局最低点,但效果还是不错的。
三、案例
API:sklearn.linear_model.LogisticRegression(penalty=‘l2’,C=1.0) #penalty指的是正则化,C使正则化力度
逻辑回归和岭回归一样,都可以L2正则化,即解决过拟合的问题。
正例:概率小的类别
反例:概率大的类别

from sklearn.linear_model import LogisticRegression
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report
import pandas as pd
import numpy as np
def logistic():
'''
逻辑回归做二分类进行癌症预测(根据细胞的属性预测)
:return:
'''
#构造列标签名字
columns=['Sample code number','id number','Clump Thickness','Uniformity of Cell Size','Uniformity of Cell Shape','Marginal Adhesion','Single Epithelial Cell Size','Bare Nuclei','Bland Chromatin','Normal Nucleoli,Mitoses','Class']
#读取数据
data=pd.read_csv("C:/Users/云丹怡/Desktop/breast-cancer-wisconsin.data",names=columns)
#将缺失值替换为np.nan
data=data.replace(to_replace='?',value=np.nan)
data=data.dropna() #直接删除缺失值数据
#分割数据
x_train,x_test,y_train,y_test=train_test_split(data[columns[1:10]],data[columns[-1]],test_size=0.25)
#标准化处理(y值不需要,因为是分类问题)
std=StandardScaler()
x_train=std.fit_transform(x_train)
x_test=std.transform(x_test)
#逻辑回归预测
lg=LogisticRegression(C=1.0)
lg.fit(x_train,y_train)
print(lg.coef_)
y_predict=lg.predict(x_test)
print('准确率=',lg.score(x_test,y_test))
print('召回率=',classification_report(y_test,y_predict,labels=[2,4],target_names=['良性','恶性']))
return None
if __name__=="__main__":
logistic()