文章目录
51 N皇后
把n个棋子放入n*n的棋盘,满足横向、竖向、斜向不能出现其他棋子。有点类似解数独,仍然采用回溯的解法
先初始化棋盘,从第一行开始“安放棋子”,每一行安放完棋子就去下一行安放棋子,棋子每一层的某一列可以选择安放棋子,因此最终的递归树,纵向是在某一行安放棋子,而横向是在某一行的某一列安放棋子。
public List<List<String>> solveNQueens(int n) {
char[][] chess = new char[n][n];
for (int i = 0; i < n; i++)
for (int j = 0; j < n; j++)
chess[i][j] = '.';
List<List<String>> res = new ArrayList<>();
solve(res, chess, 0);
return res;
}
回溯法,我们最终需要对row层col列的矩阵安放n个棋子,安放前进行校验,校验通过后对下一次进行探索。
private void solve(List<List<String>> res, char[][] chess, int row) {
if (row == chess.length) {
res.add(construct(chess));//construct就是把char[][]转换为<List<String>
return;
}
for (int col = 0; col < chess.length; col++) {
if (valid(chess, row, col)) {
chess[row][col] = 'Q';
solve(res, chess, row + 1);
chess[row][col] = '.';
}
}
}
private List<String> construct(char[][] chess) {
List<String> path = new ArrayList<>();
for (int i = 0; i < chess.length; i++) {
path.add(new String(chess[i]));
}
return path;
}
本题的核心在于校验的实现:
【1】纵向,我们从上往下“安放棋子”,因此当前位置的‘’下方”还没有安放棋子,所以只需要校验当前位置的正上方
【2】横向,我们从左往右"安放棋子”,我们一旦安放完毕棋子就直接进行往下一行放置了,因此不需要额外校验
【3】同理,对于斜边,我们只需要校验当前位置的左、右上斜边即可
//row表示第几行,col表示第几列
private boolean valid(char[][] chess, int row, int col) {
//判断当前坐标位置的上面有没有皇后
for (int i = 0; i < row; i++) {
if (chess[i][col] == 'Q') {
return false;
}
}
//判断当前坐标的右上角有没有皇后
for (int i = row - 1, j = col + 1; i >= 0 && j < chess.length; i--, j++) {
if (chess[i][j] == 'Q') {
return false;
}
}
//判断当前坐标的左上角有没有皇后
for (int i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
if (chess[i][j] == 'Q') {
return false;
}
}
return true;
}
56 合并区间
将区间数组按照左区间的值进行排序,选择第一个区间作为当前待形成区间 temp的初始值,依次和后面的区间进行比较,比较temp的右区间和另一个区间的左区间,判断二者是否可以合并。如果可以合并则更新temp的右区间(通过排序temp的左区间已经定下了),如果不可以合并,则选取新的temp继续上述过程
public int[][] merge(int[][] intervals) {
LinkedList<int[]> res = new LinkedList<>();
Arrays.sort(intervals,Comparator.comparingInt((int[] a)->a[0]));
int[] pre=intervals[0];
res.add(pre);
for (int i = 1; i < intervals.length; i++) {
if(pre[1]>=intervals[i][0]){
pre[1]=Math.max(pre[1],intervals[i][1]);
}else {
pre=intervals[i];
res.add(pre);
}
}
int[][] ans = new int[res.size()][2];
for (int i = 0; i < res.size(); i++) {
ans[i]=res.get(i);
}
return ans;
}
57 插入区间
前提:区间数组已经按照左区间排序,插入一个区间,最终输出不重叠的区间数组。(重叠则合并)
将区间分为三段处理:
【1】左边分离区间【2】右边分离区间【3】需要合并的区间
以[[1,2],[3,5],[6,7],[8,10],[12,16]]和[4,8]为例,其中[1,2]不需要处理,而[3,5]的右区间大于[4,8]的左区间,所以需要开始执行合并操作。[3,5]和[4,8]合并为[3,8],依次往后合并,最终得到[3,10]。而[12,16]属于分离右区间,不需要合并
public int[][] insert(int[][] intervals, int[] newInterval) {
//如果最终不存在合并,则需要一个新的位置存放新的区间
int[][] res = new int[intervals.length+1][2];
int index=0;
int i=0;
//左边分离区间处理
while (i<intervals.length&&intervals[i][1]<newInterval[0])
res[index++]=intervals[i++];
while (i<intervals.length&&intervals[i][0]<=newInterval[1]){
newInterval[0]=Math.min(intervals[i][0],newInterval[0]);
newInterval[1]=Math.max(intervals[i][1],newInterval[1]);
i++;
}
res[index++]=newInterval;
//继续添加右边分离
while (i<intervals.length)
res[index++]=intervals[i++];
//去除空节点
return Arrays.copyOf(res,index);
}
59 螺旋矩阵2
剑指29和LeetCode54的螺旋矩阵是给你一个矩阵,然后顺时针打印出这个序列(螺旋矩阵线性化),而本题是反过来,给你一个n,你需要将矩阵按照“螺旋矩阵”的规则进行填充(最后的数是n*n)。
其实解题思想不变,最核心的仍然是四个哨兵变量,卡住四个点,然后依次缩小包围的圈
螺旋矩阵1中,我们通过哨兵变量的定位,计算出对应的坐标,从坐标中取出元素,而本题中,我们仍然计算这个坐标,但是这时我们是往输出数组中放入元素。
public int[][] generateMatrix(int n) {
int[][] res = new int[n][n];
int a=0;
int b=0;
int c=res.length-1;
int d=res[0].length-1;
int index=1;
while (true){//一次迭代控制一次顺时针打印
//上:左》右
for(int i=a;i<=d;i++){
res[a][i]=index;
index++;
}
a++;
if(index>n*n)break;
//右:上》下
for(int i=a;i<=c;i++){
res[i][d]=index;
index++;
}
d--;
if(index>n*n)break;
//下:右》左
for(int i=d;i>=b;i--){
res[c][i]=index;
index++;
}
c--;
if(index>n*n)break;
//左:上》下
for(int i=c;i>=a;i--){
res[i][b]=index;
index++;
}
b++;
if(index>n*n)break;
}
return res;
}
60 排列序列
这题可以借助“** LeetCode31 下一个排列**”进行解决,先初始化一个最小的数字,然后拿到后面第k-1个排列。
下一个排列:
【1】从低位向高位找,找到第一个二元上升序列如12,并拿到其中的较小数min及其对应的索引minIndex
【2】从低位先高位,找到第一个大于这个较小数min的较大数max
【3】交换以上两个数,并将[minIndex+1…len-1]进行逆转操作。(minIndex+1也是较大数的位置)
例如231拿到23,交换后得到321,逆转得到312
public String getPermutation(int n, int k) {
StringBuilder sb = new StringBuilder();
for (int i = 1; i <= n; i++) {
sb.append(i);
}
String src = sb.toString();
for (int i = 1; i < k; i++) {
src = next(src);
}
return src;
}
private String next(String s){
int len = s.length();
char[] chars = s.toCharArray();
int index=len-2;
while (index>=0&&chars[index]>=chars[index+1])index--;
int temp = len-1;
while (temp>index&&chars[temp]<=chars[index])temp--;
swap(temp,index,chars);
reverse(index+1,len-1,chars);
return new String(chars);
}
64 最小路径和
和机器人行走问题如出一辙,都是每次只能向下或者向右走。机器人行走问题求得是路径数量,那么我们可以把int[][] dp看作走到(i,j)的最小路径数量 = 左边走到当前位置的路径数量 + 上面走到当前位置的路径数量。考虑的是可能路径的数量。
而本题int[][] dp就是走到(i,j)的最小路径和 = 当前位置数值 + min{左边的最小路径和 , 上面的最小路径和} ,考虑的是从具体选择头一条路径。
public int minPathSum(int[][] grid) {
int [][] dp=new int[grid.length][grid[0].length];
dp[0][0]=grid[0][0];
for (int i = 1; i < grid[0].length; i++) {
dp[0][i]+=dp[0][i-1]+grid[0][i];
}
for (int i = 1 ; i < grid.length; i++) {
dp[i][0]+=dp[i-1][0]+grid[i][0];
}
for (int i = 1; i < dp.length; i++) {
for (int j = 1; j < dp[0].length; j++) {
dp[i][j]+=Math.min(dp[i][j-1],dp[i-1][j])+grid[i][j];
}
}
return dp[dp.length-1][dp[0].length-1];
}
69 sqrt(x) ——x的平方根
前提:结果保留整数部分,小数部分舍弃
x的平方根和x的大小正相关,采用二分查找,不断缩小平方根的取值范围,如果mid*mid不等于目标值target且target在mid*mid和(mid+1)*(mid+1)的范围之间,说明当前的mid就是目标值
public int mySqrt(int x) {
if(x==0||x==1)return x;
int left=0;
int right=x;
int res = 0;
while (left<right){
int mid = (right-left)/2+left;
long cur =(long)mid*mid;
long next =(long)(mid+1)*(mid+1);
if(cur==x||(cur<x&&x<next))return mid;
else if(cur>x){
right=mid;
}else {
left=mid;
}
}
return -1;
}
71 简化路径
据说这题考的挺多的。主要解法先根据斜杠进行分片,然后使用栈做一个模拟。对应每一个“.”代表当前目录本身,忽略。而对于“…”对应的操作就是出栈(前提是栈不空),若是常规目录名就进行入栈。最后将目录依次出栈并使用斜杠拼接就是最终的简化路径
public String simplifyPath(String path) {
char[] chars = path.toCharArray();
LinkedList<String> stack = new LinkedList<>();
String[] strings = path.split("/");
for(String s:strings){
if(s.isEmpty()||s.equals("."))continue;
if(s.equals("..")){
if(!stack.isEmpty())stack.pop();
}else {
stack.push(s);
}
}
Collections.reverse(stack);
return "/"+String.join("/",stack);
}
72 编辑距离
这道题真是老朋友了,B站、小米的笔试都见过,涉及两个字符的变换,都可以试着往公共子序列方面想,而且基本可以通过打表的方式推导出状态转移方程。
理解此题的最后办法就是打表,模拟DP数组初始化的过程。
dp[i][j]就是s1[0…i]转换为s2[0…j]的最少操作数,如果s1[i]等于s2[j]那么当前位置不需要操作,次数等于s1[0…i-1]转换为s2[0…j-1]的最少操作数,被计算于dp[i-1][j-1]
而如果通过插入一个字符可以使得s1[0…i]转换为s2[0…j],那么最长操作数加一就是s1[0…i-1]转换为s2[0…j]的最小操作数+1,对应dp[i-1][j]+1。同理,删除操作对应dp[i][j-1]+1,替换操作对应dp[i-1][j-1]+1
public int minDistance(String word1, String word2) {
int len1 = word1.length();
int len2 = word2.length();
int[][] dp = new int[len1 + 1][len2 + 1];
//其中一个串是空串的情况
for (int i = 0; i <= len1; i++) {
dp[i][0]=i;
}
for (int i = 0; i <= len2; i++) {
dp[0][i]=i;
}
for (int i = 1; i <= len1; i++) {
for (int j = 1; j <= len2; j++) {
if(word1.charAt(i-1)==word2.charAt(j-1)){
dp[i][j]=dp[i-1][j-1];//当前位不改变
}else {
dp[i][j]=1+Math.min(Math.min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1]);//三种操作
}
}
}
return dp[len1][len2];
}
73 矩阵置零
原地算法,空间复杂度O(1)
在空间复杂度(m+n)下,我们使用两个矩阵去标识某一列和某一行是否存在0,而O(1)的空间复杂度,我们使用第0行和第0列进行标识工作,但是第0行和第0列本身可能存在0,因此使用另个布尔变量标识第0行和第0列是否存在零。
【1】根据第0行和第0列是否存在0,初始化两个布尔变量
【2】对非第0行和第0列部分进行布尔映射
【3】再次遍历非第0行和第0列,对于每个位置,如果任何一个映射矩阵被标记为0,则赋值为0
【4】以上初始化的都是非第0行和第0列,如果第0行或者第0列存在0,还需要对所在的0列或0行进行0赋值操作
public void setZeroes(int[][] matrix) {
boolean line=false;
boolean cow=false;
for (int[] aMatrix : matrix) {
if (aMatrix[0] == 0) {
cow = true;//第0列存在0
break;
}
}
for (int i = 0; i < matrix[0].length; i++) {
if(matrix[0][i]==0){
line=true;//第0行存在0
break;
}
}
//某个位置是0,则向矩阵相应位置进行标识
for (int i = 1; i < matrix.length; i++) {
for (int j = 1; j < matrix[0].length; j++) {
if(matrix[i][j]==0){
matrix[i][0]=0;matrix[0][j]=0;
}
}
}
//查表赋值,这时第0行0列本身的0也会被使用(但是所在的0行0列本身不被标记)
for (int i = 1; i < matrix.length; i++) {
for (int j = 1; j < matrix[0].length; j++) {
if(matrix[i][0]==0||matrix[0][j]==0){
matrix[i][j]=0;
}
}
}
//如果第一行和第一列没有0,不需要做以下两步
for (int i = 0; cow&&i < matrix.length; i++) {
matrix[i][0]=0;
}
for (int i = 0;line&&i < matrix[0].length; i++) {
matrix[0][i]=0;
}
}
75 三色国旗问题
前提:总共就三种颜色,通过原地交换使得颜色有序相邻
我们使用两个指针,zero指针指向首位,two指针指向末尾,遍历数组调整指针,最终的效果应该是两个指针将数组分成三个段,正好对应三个颜色的区域
这次,我们将源数组看作两个逻辑数组,zero数组和two数组(剩下的元素自然就放入one数组)
zero指针指向下一个要放入0的位置,当指针遍历到0的时候和zero对应元素进行交换,就相当于将元素放入到逻辑zero数组中,two指针类似但是又比较特殊,因为从two指针位置换走的不一定是1,还有可能是0,所以遍历的指针不能直接后移,当two对应元素完成交换后,向后遍历前还需要经过一次判断。
public void sortColors(int[] nums) {
int zero=0;
int two=nums.length-1;
for (int i = 0; i <=two;) {
if(nums[i]==0){
swap(nums,zero,i);
zero++;
}else if(nums[i]==2){
swap(nums,two,i);
two--;
continue;
//不能直接继续向后遍历,因为还有处理交换来的0,例如120
}
i++;
}
}
76 最小覆盖子串
非常不错的一道滑动窗口题。
我们维护一个滑动窗口,当窗口包含了(覆盖了)给定的子串,稳定期打破,左窗口向右收缩的同时结算长度。
本题的几个难点:如何判断一个字符的得到匹配(子串中可能存在重复元素),又如何判断子串被覆盖
【1】我们创建一个参考窗口 need,其中对目标子串字符以及的数量通过映射结构进行保存
【2】我们维护一个变量记录匹配字符的数量 match,每个字符能够匹配。如果子串被覆盖,那么match应该等于映射结构的大小。(仅当窗口中某个字符的数量等于参考窗口该字符的对应数量,视作匹配)
【3】同时,我们维护另一个映射结构作为窗口。
因此题目要求返回具体的字符串,因此我们不但需要维护最小覆盖串的长度,还需要维护结算该值时的开始索引。
public String minWindow(String s, String t) {
if(t.length()>s.length())return "";
int left=0;
int right=0;
int match=0;
int min = Integer.MAX_VALUE;
int start=0;
HashMap<Character, Integer> need = new HashMap<>();
for(char c:t.toCharArray())need.put(c,need.getOrDefault(c,0)+1);
HashMap<Character, Integer> window = new HashMap<>();
while (right<s.length()){
char cur = s.charAt(right);
if(need.containsKey(cur)){
window.put(cur,window.getOrDefault(cur,0)+1);
if(window.get(cur).equals(need.get(cur))){
match++;
}
}
right++;
//满足条件——窗口进入非稳定期,开始结算,并且开始移动left进行条件破坏
while (match==need.size()){
if(min>right-left){
min=right-left;
start=left;
}
char leftC = s.charAt(left);
if(need.containsKey(leftC)){
window.put(leftC,window.get(leftC)-1);
if(window.get(leftC)<need.get(leftC))match--;
}
left++;
}
}
if(min==Integer.MAX_VALUE)return "";
return s.substring(start,start+min);
}
80 删除有序数组重复项
原地算法,每个元素最多出现K次。
这种题的核心就是把原数组看作两个数组,另外是一个逻辑上的结果数组。然后维护双指针,其中fast指针就是变量源数组的指针,而lazy对应逻辑数组,lazy指向逻辑数组下一个待放入元素的位置。
因为是排序数组,所以假设第k个位置的元素是X,那么k-1 、 k-2 … 0个位置肯定都是小于X的,假设第lazy个位置的元素等于lazy-k个位置,不就说明lazy 、 lazy-1 … lazy-k这k个元素都是相同的,因此这第lazy位置的元素肯定是不能要的,lazy指针不后移 等价于 不向逻辑数组中放入元素,当下次放入元素时,lazy位置的元素被覆盖,就相当于逻辑的删除.
拿应用层面的内存举例,某个进程需要回收内存,不是将这块内存还给操作系统,而是把这块内存放入可用内存列表,或者将可用指针移动,而这块内存最终通过被覆盖而达到逻辑删除的效果。
private int removeDuplicatesK(int[] nums,int k){
int len = nums.length;
if(len<k)return len;
int lazy=k;//lazy指向下一个待放入的位置
for (int i = k; i < nums.length; i++) {
if(nums[lazy-k]!=nums[i]){
nums[lazy++]=nums[i];
}
}
return lazy;
}
84 柱状图中的最大矩形
几个月前的字节一面,上来就出个这道题,人傻了
接雨水的孪生姐妹,基本解法还是分为两种:中心扩散和单调栈,后者是主流。
接雨水是维护的是递减栈,遇到上升序列时进行结算,而本题维护递增栈,遇到下降序列时进行结算。
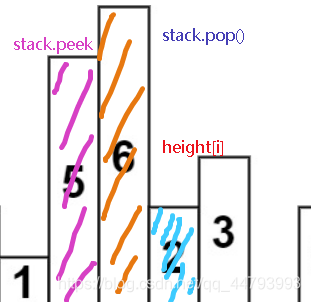
例如某一时刻栈中存放序列[1,5,6],这时遇到2则开始结算,出队得到6对应的下标,而此时stack.peek()可以拿到前一个栈内元素的下标(栈内元素并不一定在数组中连续),通过i-stack.peek()-1计算的是高度为6的块能够围出的距离。(2对应的下标i 和 5对应的下标stack.peek() 可以用于计算二者包围起来的矩阵的宽度)
6出队后,5仍然大于2于是继续上述过程,i-stack.peek()-1计算得到2,即‘以5作为高的矩阵的宽度是2.
5出队后,1小于2,于是2正常入队,此时栈中元素[1,2]
如果假如两个哨兵元素0,那么当栈为[0,1,2,3]时,遇到0一定会完成全部元素的结算。否则我们还需要对非空栈进行额外处理。
总结:
【1】维护递增单调栈,遇到下降元素则视为右边界进行结算
【2】结算某个元素时,height[stack.pop()]拿到该元素,它的结算左边界就是stack.peek()
【3】考虑此时栈是否空,根据左右边界计算出当前结算元素的矩阵宽度
【4】依次对大于下降元素的栈内元素进行结算,直到重新满足单调递增栈
(下面代码是非哨兵写法,哨兵节点解法见59题)
public int largestRectangleArea(int[] heights) {
LinkedList<Integer> stack = new LinkedList<>();
int len = heights.length;
int res = 0;
for (int i = 0; i < heights.length; i++) {
while (!stack.isEmpty()&&heights[stack.peek()]>heights[i]){
//此时i相当于右边界
int cur = stack.pop();
//O(1)获取左边界 stack.peek()
if(stack.isEmpty()){
//栈中没有元素,就是没有显式左边界,例如 3 2 1 这种情况,每次结算的宽度距离都是i
res = Math.max(res,i*heights[cur]);
}else {
res = Math.max(res,heights[cur]*(i-stack.peek()-1));
}
}
stack.push(i);
}
//如果在数组两边分别加入一个“0”作为哨兵节点,可以保证最终栈空,不需要额外后处理
while (!stack.isEmpty()){
int cur = stack.pop();
if(stack.isEmpty()){
res = Math.max(res,len*heights[cur]);
}else {
res = Math.max(res,heights[cur]*(len-stack.peek()-1));
}
}
return res;
}
85 最大矩形
84会做了,85就不难了
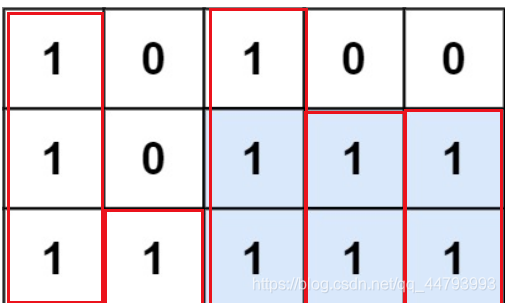
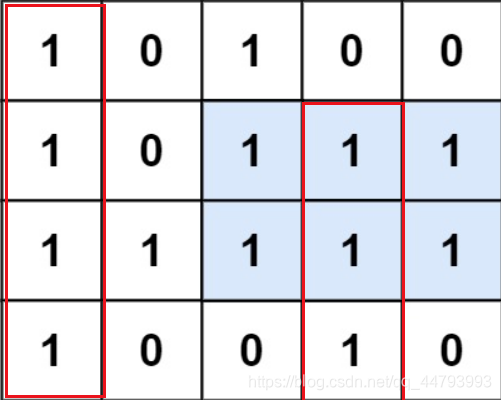
完全可以转换为第58题,只不过我们需要将矩阵构建成58题给定的输入
public int maximalRectangle(char[][] matrix) {
if(matrix==null||matrix.length==0)return 0;
int m = matrix.length;
int n = matrix[0].length;
//本题我们采用哨兵节点的写法
int[] heights = new int[n + 2];
int res=0;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if(matrix[i][j]=='1'){
heights[j+1]++;
}else {
heights[j+1]=0; //非连续柱子视为无效柱子
}
}
res=Math.max(res,maxRectangle(heights));
}
return res;
}
采用了哨兵节点的58题,不需要判空逻辑,更不需要尾处理
private int maxRectangle(int[] heights){
LinkedList<Integer> stack = new LinkedList<>();
int res=0;
for (int i = 0; i < heights.length; i++) {
while (!stack.isEmpty()&&heights[stack.peek()]>heights[i]){
res=Math.max(heights[stack.pop()] *(i-stack.peek()-1),res);
}
stack.push(i);
}
return res;
}
89 格雷编码
记公式:保留二进制的最高位作为格雷码的最高位,格雷码的其他位则通过二进制的高位和次高位异或得到(错误异或)即Gn = Bn;Gn-1 = Bn ^ Bn-1 … 依次类推(即i ^ (i >> 1))
public List<Integer> grayCode(int n) {
ArrayList<Integer> res = new ArrayList<>();
res.add(0);//格雷码序列必须0开头
for(int i=1;i<Math.pow(2,n);i++){
res.add(i^(i>>1));
}
return res;
}
91 解码方法
本题与剑指46很像,但是比它难,因为剑指46编码是从0开始的,这样210可以是2-10和21-0,但是本题的编码禁止从0开始,因此210只能被编码为2-10.
dp[i]就是前i个字符的解码数,当拿到一个二元字符串AB,如果B不是’0’,那么这个值可以单独编码,那么此时的编码次数就是dp[i-1] (dp[0]=1是用于计算,代表一个不为零的一元字符串至少能够有一种编码方式)
然后我们再考虑AB是否能编码,A不能是’0’,且AB不能大于’26’,满足该条件则说明AB可以编码,则此时的编码次数就是dp[i-2]。
如果本题没有条件限制例如剑指46则递推公式其实就是斐波那契数列,而本题有’0’的限制,因此需要有条件地添加选择项
public int numDecodings(String s) {
if(s.startsWith("0"))return 0;
int len = s.length();
int[] dp = new int[len+1];
dp[0]=1;
for(int i=1;i<=len;i++){
if(s.charAt(i-1)!='0'){
dp[i]+=dp[i-1];
}
if(i>=2 && ((s.charAt(i-2) !='0')&&s.substring(i-2,i).compareTo("26")<=0)){
dp[i]+=dp[i-2];
}
}
return dp[len];
}
93 复原IP地址
本题算是考的比较多的回溯题型,主要是本题确实是计算机网络和刷题环境的连接,可能问个IP地址就蜜汁过渡到本题了。
回溯的基本思想一致,区别就是一些剪枝和结算的细节。对于本题:
以25525511135为例,递归树横向扫描字符串,考虑如何对字符串进行切割,对于某个位置共有三种切法:切出一个长度为1的字符串、切出一个长度为2的字符串和切出一个长度为3的字符串。
纵向则是进一步的探索,对于切完字符串的下一个位置继续扫描。
对于某个切出的字符串进行判断,不符合则及时剪枝:长度大于1的字符串不能以0开头、长度为3字符串大小不能超过255.
public List<String> restoreIpAddresses(String s) {
List<String> res=new ArrayList<>();
backTrace(s,res,new ArrayList<String>(),0);
return res;
}
private void backTrace(String s ,List<String> res,List<String> ipSegments,int pos){
//切出了四个字符串后,走结算流程
if(ipSegments.size()==4 ){
if(pos==s.length())
{
res.add(String.join(".",ipSegments));
}
return;
}
//三种字符串的截取长度,每一种对应一个分叉
for (int i = 1; i < 4; i++) {
if(pos+i>s.length())break; //没法继续剪了
String cur = s.substring(pos, pos + i);
//两种无效形式:大于255或者0XX
if (cur.startsWith("0") && cur.length() > 1
|| (i == 3 && Integer.parseInt(cur) > 255))
continue;
ipSegments.add(cur);
backTrace(s,res,ipSegments,pos+i);//从下一段字符串开始截取
ipSegments.remove(ipSegments.size()-1);
}
}
94 二叉树中序遍历
栈结构模拟系统调用栈,左节点入栈模拟左子树递归,出栈模拟函数返回,此时的root就是递归第一次返回时,对应层次的root,将root指向右子树继续压栈,(模拟递归的函数调用)
public List<Integer> inorderTraversal(TreeNode root) {
LinkedList<TreeNode> stack = new LinkedList<>();
LinkedList<Integer> res = new LinkedList<>();
while(!stack.isEmpty()||root!=null){
while(root!=null){
stack.push(root);
root=root.left;
}
root = stack.pop();
res.add(root.val);
root = root.right;
}
return res;
}
95 不同的BST 2(求集合)
递归建树,分别枚举1到n,选取某个节点i作为根结点,此时左子树节点值的集合就是[start…i-1],而右子树节点值的集合就是[i+1 … n],而这些子树节点本身也需要初始化,因此我们为根树初始化之前必须要先初始化左右节点作为根的子树。(后序遍历)
创建递归函数,创建[start,end]范围内可行的BST,那么问题就可以通过递归分解为一个个子问题。如果start>end直接返回null即可,代表返回一个空节点。
拿到左右子树集合之后,分别枚举左右子树,与根节点进行组合,最终放入结果集合
public List<TreeNode> generateTrees(int n) {
if(n<1){
return new ArrayList<TreeNode>();
}
return helper(1,n);
}
private List<TreeNode> helper(int start,int end){
List<TreeNode> res =new ArrayList<TreeNode>();
if(start>end){
res.add(null);
return res;
}
for(int i=start;i<=end;i++){
List<TreeNode> left = helper(start,i-1);
List<TreeNode> right=helper(i+1,end);
//枚举左右子树,与根结点进行连接
for(TreeNode a : left){
for(TreeNode b:right){
TreeNode root =new TreeNode(i);
root.left=a;
root.right=b;
res.add(root);
}
}
}
return res;
}
96 不同的BST(求数量)
动态规划,dp[i]代表i个节点可以组成的不同BST个数。
假设有i个节点,我们根节点用去一个,我们还剩下i-1个给两边的子树使用,然后我们可以枚举不同的分配方式,最终问题转变成了计算组合数的问题。(因为是BST,因此左右组合方式的不同,其实已经决定了根结点,不需要额外讨论)
如果我们给左边分配0个节点,右边就得到i-1个节点,如果左边分配j个节点,右边就剩余i-1-j个节点
枚举的过程就是左右节点数值动态变化的过程
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0]=dp[1]=1;//空树和叶子节点都算一种
for (int i = 2; i <= n; i++) {
//枚举分配方式:左节点分配j,右节点分配i-1-j
for (int j = 0; i-1-j>=0; j++) {
dp[i]+=dp[j]*dp[i-1-j];
}
}
return dp[n];
}
97 交错字符串
动态规划,dp[i][j]表示s1[0…i]能与s2[0…j]是否能够组成s3[0…i+j]。
s1[0…i]能与s2[0…j]组成交错字符串s3[0…i+j]需要满足两个条件中任意一个:
【1】s1[i]等于s3[i+j],且s1[0…i-1]能与s2[0…j]组成交错字符串s3[0…i+j-1],这个值已经被计算在dp[i-1][j]
【2】s2[i]等于s3[i+j],且s1[0…i]能与s2[0…j-1]组成交错字符串s3[0…i+j-1],这个值已经被计算在dp[i][j-1]
public boolean isInterleave(String s1, String s2, String s3) {
int m =s1.length();
int n =s2.length();
if(m+n!=s3.length())return false;
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0]=true;
for (int i = 1; i <= m; i++) {
if(s3.charAt(i-1)==s1.charAt(i-1)){
dp[i][0]=true;
}else break;
}
for (int i = 1; i <= n; i++) {
if(s3.charAt(i-1)==s2.charAt(i-1)){
dp[0][i]=true;
}else break;
}
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
char cur = s3.charAt(i+j-1);
//s1.charAt(i-1)== cur相等后,需要继续比较s1[0...i-1]和s2[0...j]
boolean a=dp[i-1][j]&&s1.charAt(i-1)== cur;
//s2.charAt(j-1)== cur相等后,需要继续比较s1[0...i]和s2[0...j-1]
boolean b=dp[i][j-1]&&s2.charAt(j-1)== cur;
dp[i][j]=a||b;
}
}
return dp[m][n];
}
98 验证BST
最简单的方式就是中序遍历,判断遍历得到的序列是否有序,这里提供一种前序遍历的思路。
一颗BST的左子树的最大值一定是当前的根结点,而右子树的最小值一定是根结点,我们在遍历的过程中进行更新最大值或最小值,并进行范围验证即可。
public boolean isValidBST(TreeNode root){
if(root==null)return true;
if(root.left==null&&root.right==null)return true;
return dfs(root,Long.MIN_VALUE,Long.MAX_VALUE);
}
private boolean dfs(TreeNode root,long min,long max){
if(root==null)return true;
if(root.val>=max||root.val<=min)return false;
return dfs(root.left,min,root.val)&&dfs(root.right,root.val,max);
}
99 恢复二叉搜索树
前提:BST的两个节点被错误的交换,常数空间实现恢复。
例如: 1 2 3 4 5 6 ——> 1 5 3 4 2 6 需要交换 5 和 2
采用中序遍历解法,并维护两个变量用于保存需要交换的值,DFS调用返回时交换两个节点的值即可。
DFS中序遍历总是需要维护一个变量,用于保存“前置节点”的变量,当根递归层次对左子树的搜索返回时,这个变量保存的便是“顺序上的前置节点”。正常情况下root.val是一定大于这个pre.val的,因此当root.val<pre.val的情况,我们便需要保存这个异常的pre,而这时的root并不一定是需要交换的最终节点,1 5 3 4 2 6 中,由于5 2的交换,导致会进入两次判断:5 3和4 2,最终我们要拿到的就是5 和 2。因此如果不能在进入一次判断就直接返回。
public void recoverTree(TreeNode root) {
inorder(root);
int t = b.val;
b.val=a.val;
a.val=t;
}
TreeNode cur;
TreeNode a;TreeNode b;
private void inorder(TreeNode root){
if(root==null)return;
inorder(root.left);
if(cur!=null&&root.val<cur.val){
if(a==null){
a=cur;
}
b=root;
}
cur=root;
inorder(root.right);
}