题目:
In 1953, David A. Huffman published his paper "A Method for the Construction of Minimum-Redundancy Codes", and hence printed his name in the history of computer science. As a professor who gives the final exam problem on Huffman codes, I am encountering a big problem: the Huffman codes are NOT unique. For example, given a string "aaaxuaxz", we can observe that the frequencies of the characters 'a', 'x', 'u' and 'z' are 4, 2, 1 and 1, respectively. We may either encode the symbols as {'a'=0, 'x'=10, 'u'=110, 'z'=111}, or in another way as {'a'=1, 'x'=01, 'u'=001, 'z'=000}, both compress the string into 14 bits. Another set of code can be given as {'a'=0, 'x'=11, 'u'=100, 'z'=101}, but {'a'=0, 'x'=01, 'u'=011, 'z'=001} is NOT correct since "aaaxuaxz" and "aazuaxax" can both be decoded from the code 00001011001001. The students are submitting all kinds of codes, and I need a computer program to help me determine which ones are correct and which ones are not.
Input Specification:
Each input file contains one test case. For each case, the first line gives an integer?N?(2≤N≤63), then followed by a line that contains all the?N?distinct characters and their frequencies in the following format:
c[1] f[1] c[2] f[2] ... c[N] f[N]where?c[i]?is a character chosen from {'0' - '9', 'a' - 'z', 'A' - 'Z', '_'}, and?f[i]?is the frequency of?c[i]?and is an integer no more than 1000. The next line gives a positive integer?M?(≤1000), then followed by?M?student submissions. Each student submission consists of?N?lines, each in the format:
c[i] code[i]where?c[i]?is the?i-th character and?code[i]?is an non-empty string of no more than 63 '0's and '1's.
Output Specification:
For each test case, print in each line either "Yes" if the student's submission is correct, or "No" if not.
Note: The optimal solution is not necessarily generated by Huffman algorithm. Any prefix code with code length being optimal is considered correct.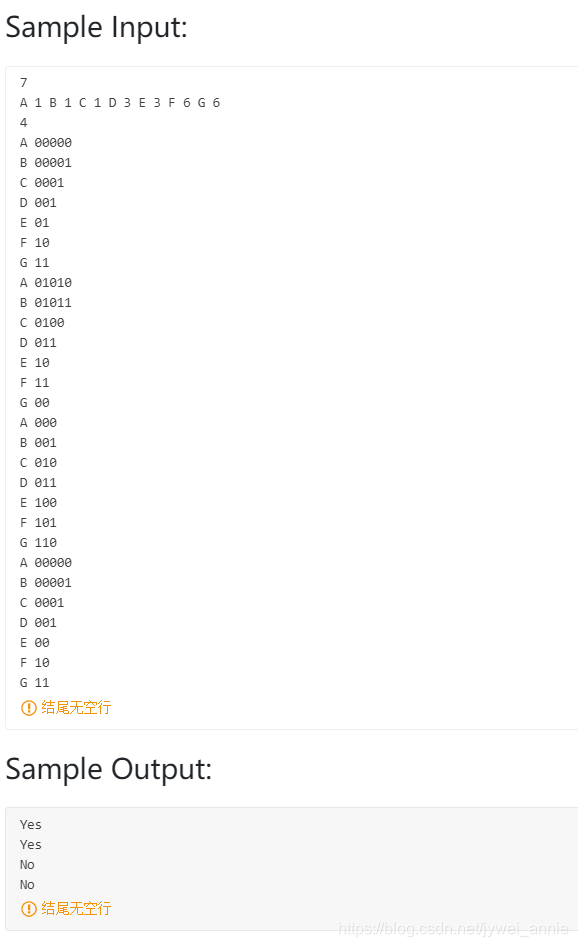
题目大意:给定一组编码,判断其是否是霍夫曼编码。
解题思路:
? ? ? ? 通过两个标准来判断给出的编码是否是霍夫曼编码。
? ? ? ? 1.首先计算出最短编码长度,此时不必使用二叉树的形式来计算,利用规律直接计算可得;具体方法可参考(13条消息) (2016-3)字符串的哈夫曼编码长度_julia7_的博客-CSDN博客;
? ? ? ? 2.通过给出的编码构造出二叉树,“0”代表向左,“1”代表向右,到达目标位置后,将目标位置的元素标定为1,若目标位置已经存在标定则表示编码重复;构建出二叉树后,确认是否所有目标位置都在二叉树上的叶节点上,即他们的左指针和右指针都是NULL。
整体代码:
#include<iostream>
#include<cstring>
using namespace std;
//extern char c[64] = {0};
//extern int f[64] = {0};
//extern int a[64] = {0};
extern int N = 0;
typedef struct wordandfre* WF;
struct wordandfre {
char c;
int fre;
string position;
};
typedef struct HTree* HT;
struct HTree {
int i;
HT left;
HT right;
};
void order(int a[], int n)
{
for (int i = 0; i < n - 1; i++) {
bool isSorted = true;
for (int j = 0; j < n - 1 - i; j++) {
if (a[j] < a[j + 1]) {
isSorted = false;
int temp = a[j];
a[j] = a[j + 1];
a[j + 1] = temp;
}
}
if (isSorted) break;
}
}
int testleaf(HT H) { //测试是否所有点都在叶节点上
if (H) {
if (H->i == 1 && (H->left || H->right)) return 1;
return(testleaf(H->left) ||testleaf( H->right));
}
return 0;
}
int test(wordandfre wf[]) { //根据position构造二叉树
HT H = NULL;
H = (HT)malloc(sizeof(struct HTree));
H->i = 0;
HT S=NULL;
S = (HT)malloc(sizeof(struct HTree));
H->left = S;
S->left = NULL;
S->right = NULL;
H->right = NULL;
//H->left= (HT)malloc(sizeof(struct HTree));
for (int i = 0; i < N; i++) {
S = H->left;
if (!S) {
S = (HT)malloc(sizeof(struct HTree));
S->left = NULL;
S->right = NULL;
}
for (int j = 0; j < wf[i].position.length(); j++) {
if (wf[i].position[j]=='1') {
if (!(S->right)) {
S->right = (HT)malloc(sizeof(struct HTree));
//S->left = NULL;
//S->right = NULL;
S->right->left = NULL;
S->right->right = NULL;
}
S = S->right;
//S->i = 0;
}
else {
if (!(S->left)) {
S->left = (HT)malloc(sizeof(struct HTree));
//S->left = NULL;
S->left->left = NULL;
S->left->right = NULL;
//S->right = NULL;
}
S = S->left;
//S->i = 0;
}
}
if (S->i == 1) return 1;
else S->i = 1;
}
return testleaf(H);
}
int findNo(wordandfre wf[],char x) {
for (int i = 0; i < N; i++) {
if (wf[i].c == x) return i;
}
return -1;
}
int main() {
int ans=0,T,ANS=0,judge;
char x;
wordandfre wf[64];
cin >> N;
int a[64];
for (int i = 0; i < N; i++) {
cin >> wf[i].c >> wf[i].fre;
a[i] = wf[i].fre;
}
int M = N;
while (M>1) {
order(a ,N);
ans = ans + a[M - 1] + a[M - 2];
a[M - 2] = a[M - 1] + a[M - 2];
a[M - 1] = 0;
M--;
}//计算出ans为最小路径长度
cin>>T;
for (int j = 0; j < T; j++) {
ANS = 0;
for (int k = 0; k < N; k++) {
cin >> x;
int num = findNo(wf, x);
cin >> wf[num].position;
ANS = ANS + wf[num].fre * wf[num].position.length();
}
if (ANS != ans) judge = 1;//判断给出的代码长度和霍夫曼编码是否相等
else {
judge = test(wf);;
}
//judge = test(wf);
if (judge == 0) cout << "Yes";
else cout << "No";
}
return 0;
}
本题的重难点在于构造二叉树,即函数test:
int test(wordandfre wf[]) { //根据position构造二叉树
HT H = NULL;
H = (HT)malloc(sizeof(struct HTree));
H->i = 0;
HT S=NULL;
S = (HT)malloc(sizeof(struct HTree));
H->left = S;
S->left = NULL;
S->right = NULL;
H->right = NULL;
//H->left= (HT)malloc(sizeof(struct HTree));
for (int i = 0; i < N; i++) {
S = H->left;
if (!S) {
S = (HT)malloc(sizeof(struct HTree));
S->left = NULL;
S->right = NULL;
}
for (int j = 0; j < wf[i].position.length(); j++) {
if (wf[i].position[j]=='1') {
if (!(S->right)) {
S->right = (HT)malloc(sizeof(struct HTree));
//S->left = NULL;
//S->right = NULL;
S->right->left = NULL;
S->right->right = NULL;
}
S = S->right;
//S->i = 0;
}
else {
if (!(S->left)) {
S->left = (HT)malloc(sizeof(struct HTree));
//S->left = NULL;
S->left->left = NULL;
S->left->right = NULL;
//S->right = NULL;
}
S = S->left;
//S->i = 0;
}
}
if (S->i == 1) return 1;
else S->i = 1;
}
return testleaf(H);
}? ? ? ?申请空间的位置尤为重要,如果在已经有值之后重修申请空间则会导致,原本互相连接的节点失效。
? ? ? ?其次之前一直出现的问题是无法将0xcdcdcdcd判断为空,事实上,即使为空,我们也需要首先定义S=NULL,才能在if语句中用if(!S)z作为判断的依据,详细可参考(13条消息) 读取访问权限冲突。0xCDCDCDCD_Ray_Ding的博客-CSDN博客_读取访问权限冲突0xcdcdcdcd
结果展示: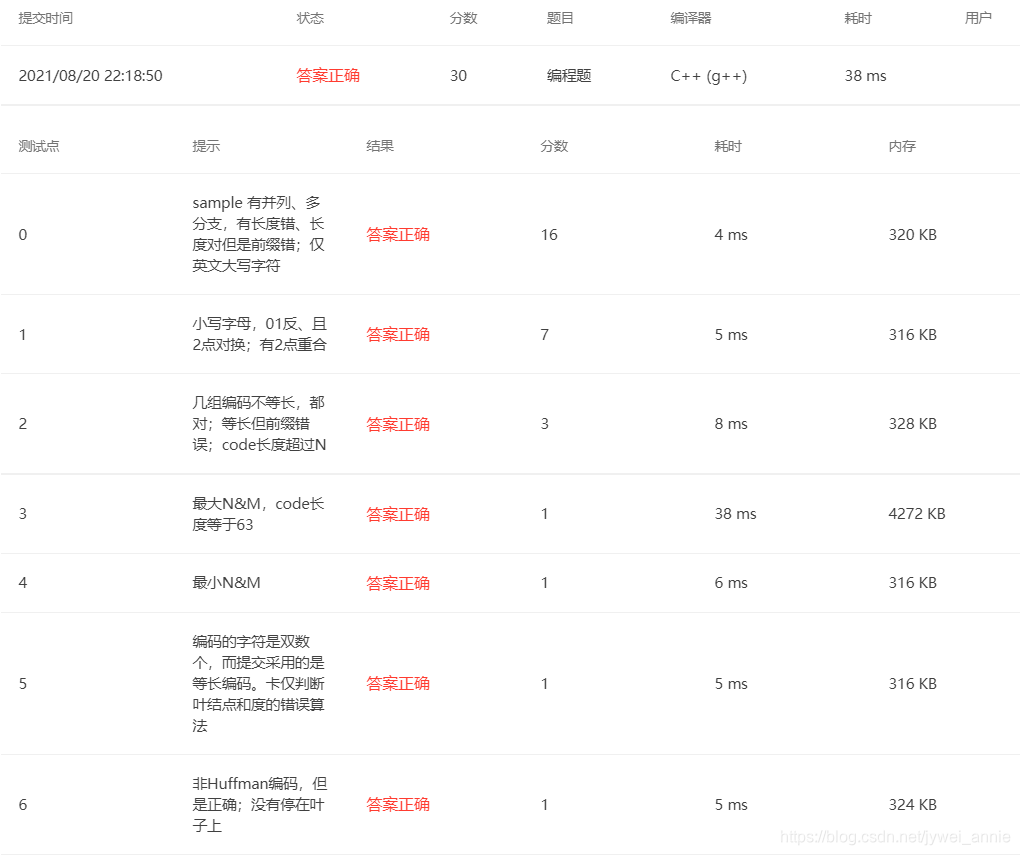
?曾错原因:
? ? ? ? sample2错了,原因是没有考虑到编码完全重复的情况,只看了不同编码是否有二义性。