参考:数据结构与算法基础(青岛大学-王卓)
传送门:
数据结构与算法_【1】概念引入(C++实现)
数据结构与算法_【2】线性表(顺序表链表)(C++实现)
数据结构与算法_【3】栈和队列(C++实现)
数据结构与算法_【4】串数组广义表(C++实现)
数据结构与算法_【5】树和二叉树(C++实现)
数据结构与算法_【6】树和森林(C++实现)
数据结构与算法_【7】哈夫曼树(C++实现)
数据结构与算法_【8】图(C++实现)
数据结构与算法_【9】查找(C++实现)
数据结构与算法_【10】排序(C++实现)
排序
排序就是将无序序列排成一个有序序列
若结点包含多个数据域,排序一般是对于某一个数据域而言的
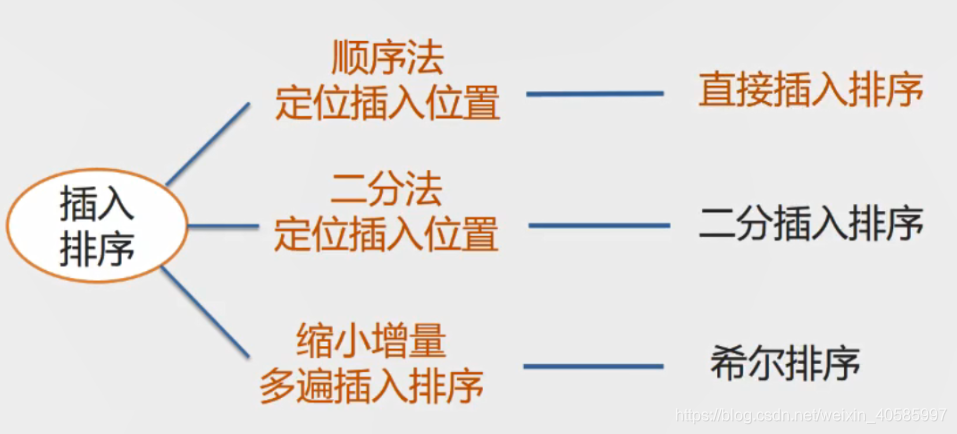
排序方法分类:
1 插入排序-直接插入排序
边插入边排序,保证子序列中随时都是排好序的。
1.1 直接插入排序
代码:
void InsertSort(SeqList<int>& L)
{
int i, j;
for (i = 2; i < L.size; i++)
{
if (L.elem[i] < L.elem[i - 1])
{
L.elem[0] = L.elem[i];//哨兵记录需要插入的元素
for (j = i - 1; L.elem[j] > L.elem[0] && j>=1 ;j--)
{
L.elem[j + 1] = L.elem[j];
}
L.elem[j + 1] = L.elem[0];//当哨兵值小于当前值,跳出循环,当前索引+1位置插入元素
}
}
L.elem[0] = 0;
//L.ShowList();
}
性能分析:
2 插入排序-折半插入排序
代码:
void BInsertSort(SeqList<int>& L)//折半插入排序
{
int i, j;
for (i = 2; i < L.size; i++)
{
L.elem[0] = L.elem[i];
int low = 1;
int high = i - 1;
while (low <= high)
{
int mid = (low + high) / 2;
if (L.elem[0] < L.elem[mid])
{
high = mid - 1;
}
else
{
low = mid + 1;
}
}
for (j = i - 1; j >= high + 1; j--)
{
L.elem[j + 1] = L.elem[j];
}
L.elem[high + 1] = L.elem[0];
}
L.elem[0] = 0;
}
性能分析:
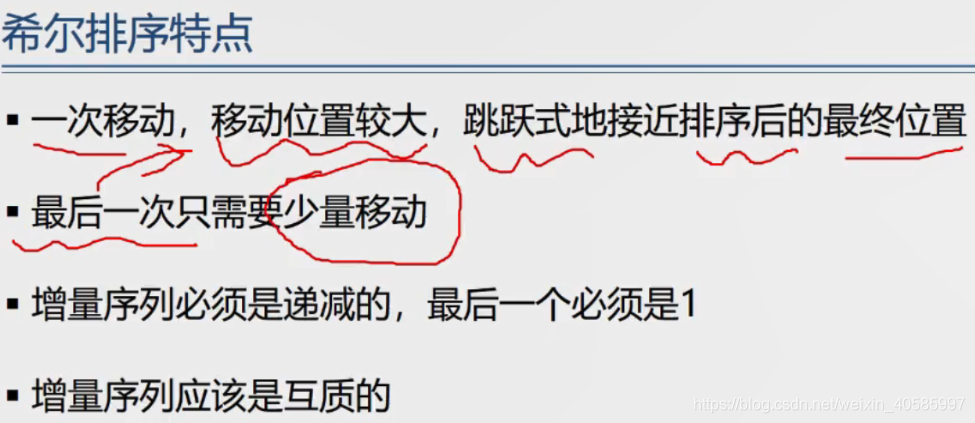
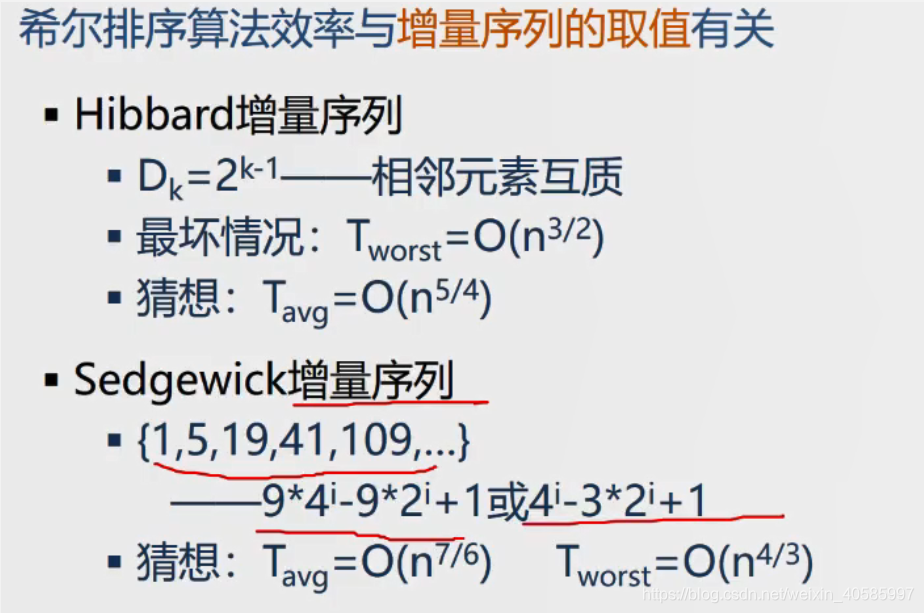
3 插入排序-希尔排序
代码:
void ShellInsert(SeqList<int>& L, int dk)
{
int i, j;
for (i = dk + 1; i < L.size; i++ )
{
L.elem[0] = L.elem[i];
if (L.elem[i] < L.elem[i - dk])
{
for (j = i - dk; j >= 1 && L.elem[0] < L.elem[j]; j=j-dk)
{
L.elem[j + dk] = L.elem[j];
}
L.elem[j + dk] = L.elem[0];
}
}
}
void ShellSort(SeqList<int>& L)
{
int dlta[5] = { 1,3,5,7,11 };
int t = 4;
for (int i = 0; i < t; i++)
{
ShellInsert(L, dlta[i]);
}
L.elem[0] = 0;
}
性能分析:
4 交换排序-冒泡排序
代码:
void BubbleSort(SeqList<int>& L)
{
int i, j, temp;
for (i = 1; i < L.size; i++)//帮助确定j需要遍历多少数据
{
for (j = 1; j < L.size - i; j++)
{
if (L.elem[j] > L.elem[j+1])//若为逆序,交换
{
temp = L.elem[j];
L.elem[j] = L.elem[j+1];
L.elem[j] = temp;
}
}
}
}
改进的冒泡排序:
void BubbleSort(SeqList<int>& L)使用flag标志改进冒泡排序
{
int i, j, temp;
int flag = 1;
for (i = 1; i < L.size && flag==1 ; i++)//帮助确定j需要遍历多少数据
{
flag = 0;//如果有一次没有发生逆序,flag=0,跳出外层循环!
for (j = 1; j < L.size - i; j++)
{
if (L.elem[j] > L.elem[j+1])//若为逆序,交换
{
temp = L.elem[j];
L.elem[j] = L.elem[j+1];
L.elem[j] = temp;
flag = 1;
}
}
}
}
性能分析:
5 交换排序-快速排序
代码:
//Partition 隔断
int Partition(SeqList<int>& L, int low, int high)//快速排序子程序
{
//L.elem[0] = L.elem[low];
int pivotkey = L.elem[low];
while (low < high)
{
while (low < high && pivotkey <= L.elem[high]) high--;//如果右边元素一直大于隔断元素,则右索引--
L.elem[low] = L.elem[high];//右边元素小于隔断值,跳出循环,将元素放在左边
while (low < high && pivotkey >= L.elem[low]) low++;
L.elem[high] = L.elem[low];
}
L.elem[low] = pivotkey;
return low;
}
void Qsort(SeqList<int>& L,int low,int high)//快速排序
{
if (low < high)
{
int pivotloc = Partition(L, low, high);
Qsort(L, low, pivotloc - 1);
Qsort(L, pivotloc + 1, high);
}
}
性能分析:
是一种不稳定的排序方法!
快速排序不适于对原本有序或者基本有序的记录序列进行排序!
6 选择排序-简单选择排序
代码:
void SelectSort(SeqList<int>& L)
{
for (int i = 1; i <= L.size - 1; i++)
{
int k = i;
for (int j = i + 1; j <= L.size - 1; j++)
{
if (L.elem[k] > L.elem[j])
{
k = j;//记录最小值的位置
}
}
if (k != i)
{
//如果最小值位置不是i,交换i、k
int temp = L.elem[i];
L.elem[i] = L.elem[k];
L.elem[k] = temp;
}
}
}
性能分析:
修改程序可以变为稳定的!
7 选择排序-堆排序
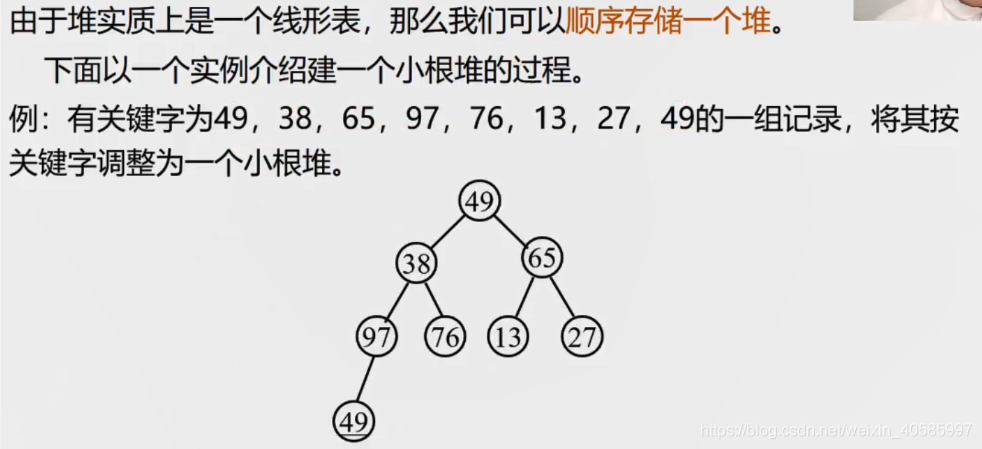
堆:
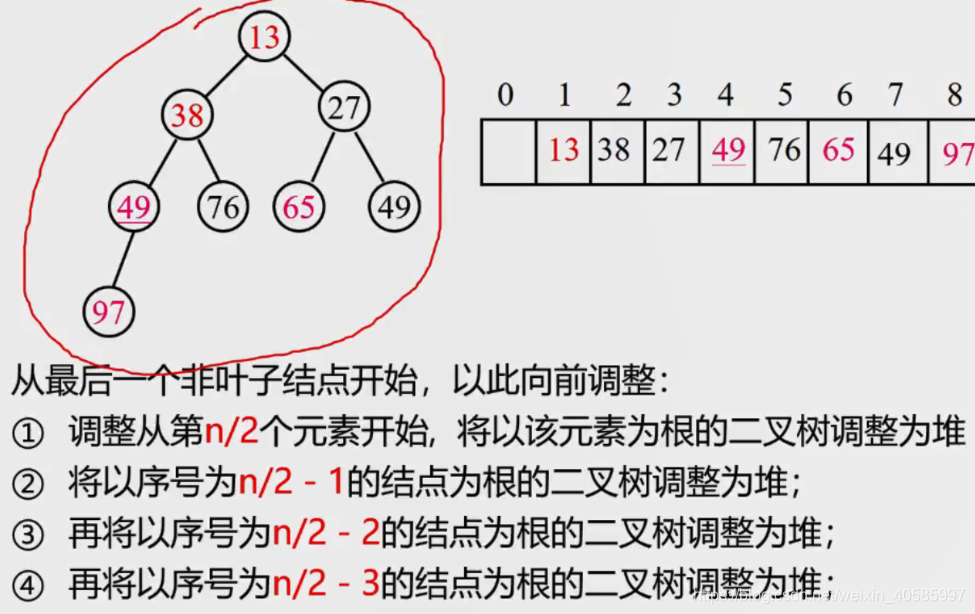
堆的调整:
性能分析:











![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5RK0Rbhs-1629460006974)(%E6%95%B0%E6%8D%AE%E7%BB%93%E6%9E%84%E4%B8%8E%E7%AE%97%E6%B3%95%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B010_%E6%8E%92%E5%BA%8F_md_files%5Cimage%20%2813%29.png?v=1&type=image)]](https://img-blog.csdnimg.cn/f4ee3be10eea417484af9319c5f6621e.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MDU4NTk5Nw==,size_16,color_FFFFFF,t_70)