硬核数据结构——链表Js
1.链表的基本概念
1.链表存储有序的元素集合,不同于数组的是链表中的元素在内存中并不是连续放置的,每一个元素由一个存储元素本身的节点和指向下一个元素的指针组成。
2.链表的优势:添加或者删除元素时,不需要移动其他元素
3.数组与链表访问元素不同点:数组拿到索引可以直接访问数组中的元素,链表想要访问一个元素时,需要从表头(起点)开始迭代直到找到这个元素。
4.链表一般分为单向链表,双向链表,环形链表
2.双向链表以及环形链表
1.单向链表:元素由一个存储元素本身的节点和指向下一个元素的指针所组成,如下图所示:
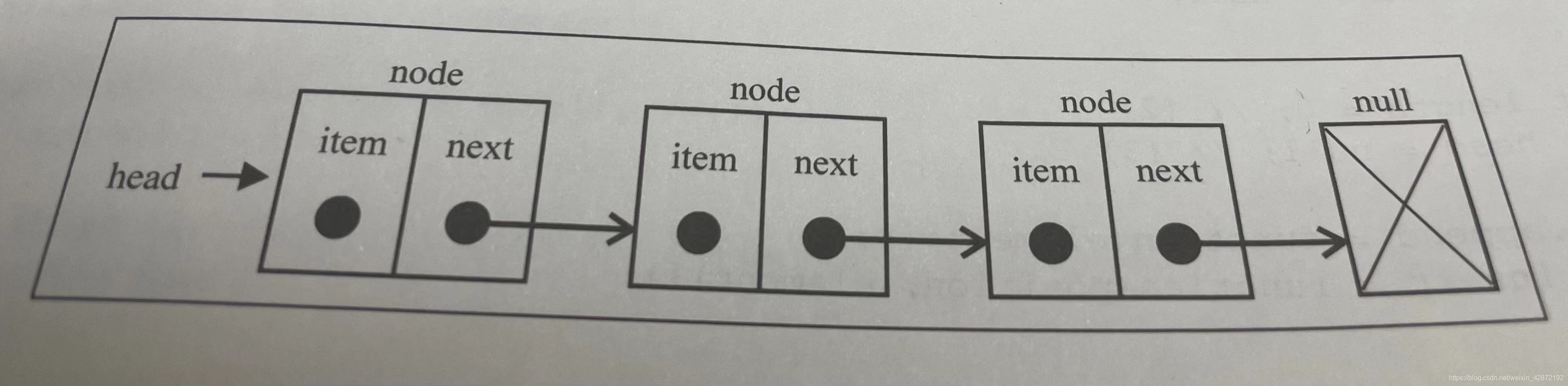
2.双向链表:与单向链表不同的是,除了一个存储元素本身的节点外,在双向链表中,链接是双向的,一个链向下一个元素,另一个链向前一个元素。如下图所示:
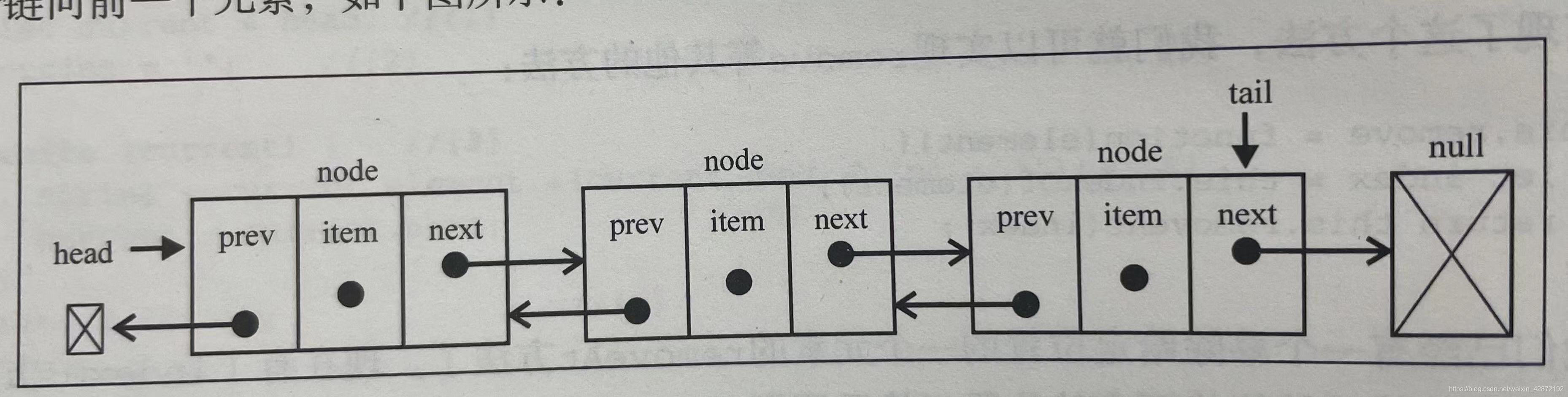
3.循环链表:可以像单向链表一样只有单向引用,也可以像双向链表一样有双向引用,循环链表和链表唯一的区别就是,最后的一个元素指向下一个元素的指针不同,链表最后一个元素指针指向null,环形链表最后一个元素指针指向第一个元素或者其他元素。如下图所示:
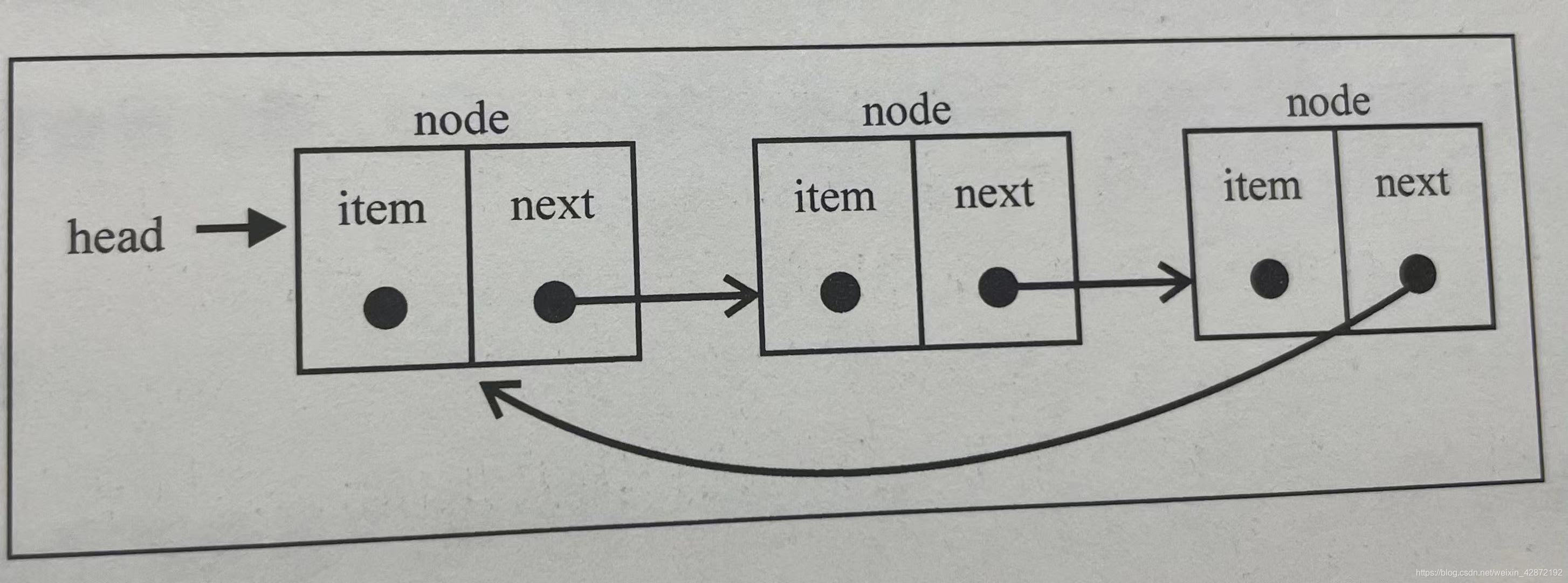
3.链表数据结构实现
export default class LinkedList<T> {
protected count = 0;
protected head: Node<T> | undefined;
constructor(protected equalsFn: IEqualsFunction<T> = defaultEquals) {}
push(element: T) {
const node = new Node(element);
let current;
if (this.head == null) {
// catches null && undefined
this.head = node;
} else {
current = this.head;
while (current.next != null) {
current = current.next;
}
current.next = node;
}
this.count++;
}
getElementAt(index: number) {
if (index >= 0 && index <= this.count) {
let node = this.head;
for (let i = 0; i < index && node != null; i++) {
node = node.next;
}
return node;
}
return undefined;
}
insert(element: T, index: number) {
if (index >= 0 && index <= this.count) {
const node = new Node(element);
if (index === 0) {
const current = this.head;
node.next = current;
this.head = node;
} else {
const previous = this.getElementAt(index - 1);
node.next = previous.next;
previous.next = node;
}
this.count++;
return true;
}
return false;
}
removeAt(index: number) {
if (index >= 0 && index < this.count) {
let current = this.head;
if (index === 0) {
this.head = current.next;
} else {
const previous = this.getElementAt(index - 1);
current = previous.next;
previous.next = current.next;
}
this.count--;
return current.element;
}
return undefined;
}
remove(element: T) {
const index = this.indexOf(element);
return this.removeAt(index);
}
indexOf(element: T) {
let current = this.head;
for (let i = 0; i < this.size() && current != null; i++) {
if (this.equalsFn(element, current.element)) {
return i;
}
current = current.next;
}
return -1;
}
isEmpty() {
return this.size() === 0;
}
size() {
return this.count;
}
getHead() {
return this.head;
}
clear() {
this.head = undefined;
this.count = 0;
}
toString() {
if (this.head == null) {
return '';
}
let objString = `${this.head.element}`;
let current = this.head.next;
for (let i = 1; i < this.size() && current != null; i++) {
objString = `${objString},${current.element}`;
current = current.next;
}
return objString;
}
}
export class Node<T> {
constructor(public element: T, public next?: Node<T>) {}
}
export class DoublyNode<T> extends Node<T> {
constructor(
public element: T,
public next?: DoublyNode<T>,
public prev?: DoublyNode<T>
) {
super(element, next);
}
}
export function defaultEquals<T>(a: T, b: T): boolean {
return a === b;
}
export type IEqualsFunction<T> = (a: T, b: T) => boolean;
需要添加一个Node辅助类,Node表示链表中的项,包含element属性,即添加到该项的值,以及一个next属性,下一个节点的指针,prev双向链表的新增指针(稍后解释)
push() 向列表尾部增加一个新的项
getElementAt() 获取当前链表中的尾项
insert() 向链表的特定位置添加一个新的项
removeAt() 向链表的特定位置移除一个项
remove() 链表移除一个项,头部移出(首位)
indexOf() 获取链表中的某项
isEmpty() 判断链表中是否空
size() 链表的长度
getHead() 获得链表的头部(首位),
clear() 清除链表
toString() 将链表转为一个字符串输出
4.链表是否有环
针对链表问题,我们经常会遇到判断一个链表是否有环,这个在面试中出现的频率也比较高,接下来简单说说
最常用的方式就是快慢指针,在链表的头节点分别放两个指针,一个指针慢(a表示),一个指针快(b表示),a每次移动一个位置,b移动两个位置,如果相遇则说明有环,如果不相遇则说明无环。
问:链表再有环的情况下如何能够知道链表的环入口点?
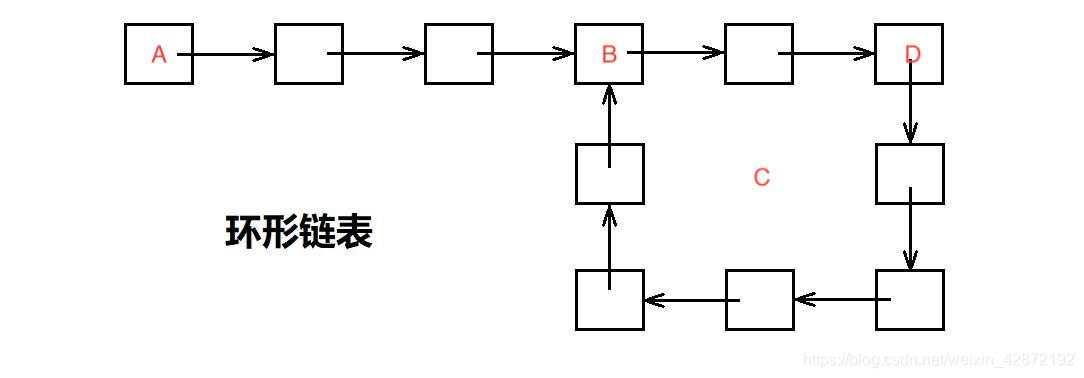
假设D为快慢指针相遇点
假设链表头部(A)到环口(B)的距离为 a
假设链表环口(B)到快慢指针的相遇点(D)的距离为 b
假设环的长度为 c
快指针总距离:d(fast) = a + b + c
慢指针总距离:d(slow) = a + b
因为快指针的速度是慢指针的两倍,相同时间,因此2倍的慢指针总距离等于快指针总距离,则:2*d(slow)=d(fast)
得:a=c-b
可以得到结论:链表头、相遇点各设一个指针,指针每次都各走一步,两个指针必定相遇,且相遇第一点为环入口点
代码如下:
var LinkedListCycle = function (head) {
let p1 = head; // 慢指针
let p2 = head; // 快指针
while (p1 && p2 && p2.next) {
p1 = p1.next;
p2 = p2.next.next;
if (p1 === p2) { // 是否有环
p2 = head; //重新从开始找,每次一步,再相遇就是入口
while (p2 != p1) {
p1 = p1.next;
p1 = p1.next;
}
return fast;
}
}
return null; // 当循环结束不重复,则没环
};