[数据结构与算法]红黑树的详解

1. 红黑树的提出

友情提示：本文需要在了解平衡二叉树、AVL树和B-树的背景下阅读，如果对这三个数据结构还不了解的小伙伴可以读一下我的另外三篇文章：【数组模拟二叉搜索树（二叉排序树）】、【数组模拟AVL树（平衡二叉树）】、【B-树的详解】。

既然平衡树家族中已经有了AVL树这种成员，并且其时间复杂度已经达到了 $O(logh)$ 的要求，那么为啥要提出红黑树呢？

我们来回顾一下AVL树的操作：

1. 插入操作：在AVL树中插入一个数，只要经过一次 $O(1)$ 的旋转操作，AVL树局部乃至整个树的高度都能够复原。
2. 删除操作：在AVL树中删除一个数，有可能自底而上逐层引发 $logh$ 次的 $O(1)$ 旋转，导致树型拓扑结构的剧烈变化。

因此，在涉及到大量的动态操作时，我们希望其引发的结构变化量不超过 $O(1)$，对树型拓扑结构的影响都能控制在常数的范围之内。而红黑树，就是这样的一种树型结构。

2. 红黑树的定义

红黑树是由红、黑两类结点组成的二叉搜索树，和B-树类似，红黑树将所有的内部结点都增设了外部结点NULL，如下图。

定义规则可以总结为如下几点：

1. 树根：必须为黑色（只针对非空红黑树）
2. 外部结点：均为黑色（实际上外部结点根本不必存在，引入外部结点只是便于红黑树的分析）
3. 内部结点：若为红，则结点的孩子、父亲必为黑
4. 外部结点到根：途中经过的黑结点数目相等，又称为黑深度（这就是红黑书的“平衡”）

如果将红黑树比作人，可以将树根看成人的帽子，外部结点看做人的靴子，下图是一棵红黑树。

细心的同学可以发现，图中并没有所谓的“外部结点”，其实外部结点本质不存在，其定义只是便于我们分析红黑树，下图中手工标注了三个外部结点（外部结点颜色是黑）。

在红黑树中任意两个不同的外部结点到达根结点的路径中，经过的黑结点数量一定相同，如下图，都是三个。

上面大致介绍了一下红黑树的定义和相关规则，但是相信各位同学还是一头雾水，这个红黑树为啥要这么玩？

那么，有没有什么更为直观的解释呢？这里，为了更好的理解红黑树，我们要先介绍一种树型结构的另一种等价拓扑变换—提升变换。

提升变换：将每一个红色结点从视觉上提升到其黑色的父亲结点一侧，如下图：

经过红色结点上升操作之后，绝对不会出现两个红色结点紧挨着的情况，即便并列，中间也必然夹有一个黑色结点，也就是他们的父亲结点。

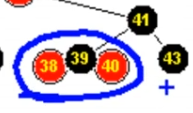
下图是变换之前的某棵红黑树：

所有的红色结点提升到父亲结点旁边之后，如下图（蓝色圈圈只是圈出了部分）：

看到现在，相信你已经有点“感觉”了。别急，我们再继续看一个更大的实例，请特别注意底层的叶子结点，目前都是高低错落此起彼伏的：

经过红色结点提升变换后，所有底层的叶子结点都变成了沿统一水平高度平齐的高度：

尽管红黑树的规则看起来“高深莫测”，但是经过红色结点提升变换之后，他的结构就更加清晰明了。

提升各个红色结点，使之与其父亲黑色结点等高，从这个角度来看，每一棵红黑树就是4阶的B-树，也就是(2, 4)-树，如果你对B-树不熟悉，可以看我的另一篇博客：【B-树的详解】。

因此我们只需要将红黑树中的黑色结点与其上提的红色孩子（关键字合并）视作4阶B-树中的一个结点 ，根据黑色根结点左右孩子的颜色分为四种组合，每种组合分别对应于4阶B-树的一类内部结点：

上面的图中，我们特别用虚线标出黑色结点指向红色结点的原因是：因为红黑树平衡的关键在于黑高度的统一，红色结点的存在其实对黑高度的计算没有贡献。

3. 红黑树的查找

红黑树的查找操作和传统的二叉搜索树一致，这里不再赘述。

4. 红黑树的插入

与了解红黑树的定义一样，我们会发现红黑树和与其对应的“影子B-树”之间的关系非常好理解，而且反过来也是如此，这样理解红黑树的原理表面看来有点迂回，但我们很快就会感受到，这种间接的理解方式学习红黑树反而是效率最高的。

4.1 插入操作的算法框架

1. 首先，传入待插入的关键字 $e$ （不妨假设树中原来不存在 $e$）

2. 按照二叉搜索树的常规插入算法，插入关键字， $x=insert(e)$ ，$x$ 必为末端结点，不妨假设 $x$ 的父亲 $p=x\to parent$ 存在；如果不存在，就是简单的首次插入

3. 将 $x$ 染红（除非它是根），如下图：
   【解释】因为这样做的话，现在可以保证树根结点还是黑色、外部结点依然是黑的、根结点通往外部结点的路径上黑结点的数目依然不变，但是这一步有可能导致两个红色结点成为父子，因为其父结点 $p$ 颜色不确定。
   
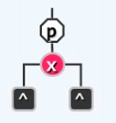
   如果此时父亲结点 $p$ 为黑色，则插入成功，函数结束。否则两个红色结点连在了一起，称之为双红缺陷，需要调整。

4. 如果出现了双红缺陷，需要通过后续介绍的调整处理，如下图：
   
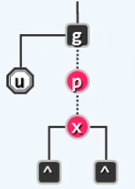
   【解释】：之所以把连接到红色结点的边标记为虚线，是因为后面需要将红色结点提升。

5. 插入操作完成

下面，重点介绍插入中双红缺陷的处理办法：

先分析一波：

先考察 $x$ 的祖父结点 $g=p\to parent$ ，注意这里的祖父结点 $g$ 一定是存在的，否则 $p$ 不会为红色，并且祖父结点 $g$ 一定为黑色。

然后，我们还要考察 $g$ 的另外一个孩子 $u$，相对于 $x$ 而言。结点 $u$ 是 $x$ 的叔父，当然，结点 $u$ 的颜色也是不定的，我们要根据结点 $u$ 的颜色分别处理。

4.2 调整：双红缺陷

4.2.1 双红缺陷1：叔父结点 u 是黑色

此时， $x$, $p$, $g$ 的四个子树的根（可能是外部结点）必定全部为黑，且黑高度相同，依据 $x$ 在 $p$ 的左右关系，可以分为下面两种情况。

当然，依据 $p$ 在 $g$ 的左右关系会产生和上图中对称的另外两种情况，但是原理是一样的，这里不再赘述。

为了更好的研究这两种红色缺陷，我们将红色结点提升：

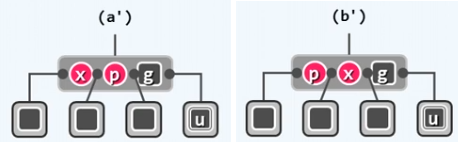
可以看到，我们结点“合并”之后，其所有的孩子，并没有出现超过4阶B-树上界的情况，唯一的缺点是“合并”以后的结点根结点是红色而不是黑色的，造成了两个红色相邻的违规现象。因此，从B-树的角度看，这种调整非常简明，我们并不需要调整B-树的拓扑结构，而仅仅需要对违规的关键字进行重新染色即可。

对于处理 $(a^{\prime })$ 中的情况，只需要交换 $p$ 和 $g$ 的颜色即可。同理，$(b^{\prime })$ 中的情况，只需要交换 $x$ 和 $g$ 的颜色即可。

我们刚刚这种角度实际上是将其用B-树的角度来处理双红缺陷，如果用这种方式处理的话，还要分情况讨论是 $p$ 还是 $x$ 去与 $g$ 交换颜色，再结合尚未列出的两个镜像的情况，共4种不同的交换颜色的处理方式，分类讨论很麻烦。

实际中真正处理叔父结点是黑色情况下的双红缺陷的办法：

在实际操作中，只要是出现了双红缺陷，并且 $x$ 的叔父 $u$ 是黑色，统一采用下面步骤处理双红缺陷：

（1）参考AVL树算法，做局部的重构，将结点 $x$、$p$、$g$ 这三个结点以及它们下属的四棵子树找出来，这里可以结合图$(a)$，然后从 $g$ 对这一局部开始中序遍历，获得一个中序遍历的有序序列：$[T_0<a<T_1<b<T_2<c<T_3]$，从新构建排布方式：

（2）直接将中间结点 $b$ 染黑，$a$ 和 $c$ 染红，如下图。

那么上面这个骚操作为什么行得通呢？如果放在B-树中又如何解释呢？

首先，调整之前之所以非法，是因为在(2,4)-树中某个三叉结点中插入了红色的关键字形成了四叉结点，使得原来黑色的关键字不再居中，形成了RRB或BRR，出现了相邻的红色关键字，也就是双红缺陷。

而调整之后的效果相当于B-树的拓扑结构不变，但是在新的四叉结点中，三个关键字的颜色改为RBR。

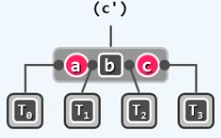
这个操作的时间复杂度是常数的。

4.2.2 双红缺陷2：叔父结点 u 是红色

还是老方法，想要分析清楚红黑树，先转换为B-树，让所有红色结点提升，如下图：

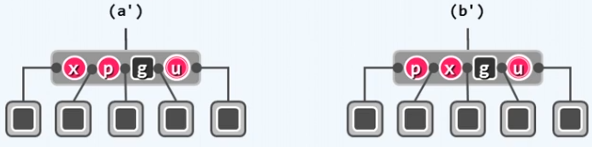
可以看出，提升之后一个4阶B-树结点中出现了4个关键字，对应于5个分支，这种情况下红黑树的双红缺陷等价于B-树中的结点发生了上溢。

因此，与其说我们是在红黑树中修复双红缺陷，不如说我们在4阶B-树中修复上溢缺陷，这二者完全是一回事，见下图。

我们结合上图具体介绍一下叔父为红色的双红缺陷处理办法：

（1）先将红色结点上升，得到如 $(b^{\prime })$ 所示的效果

（2）计算 $s=?\frac{4}{2}?=2$，我们将 $[k_0,k_1,k_2,k_3]$ 中的 $k_s=k_2$ 上提到该上溢结点的父结点中，将 $[k_2]$ 由黑色染成红色（相当于对上溢结点的父结点插入一个新的结点，所以要染成红色） ，同时将其原来的左右孩子染成黑色（因为红色结点的孩子都是黑色）即可。

（3）我们说将 $k_2$ 染红并且上提看做作为新结点插入到上溢结点的父结点，因此上溢的结点的父结点有可能因为这个插入也发生双红缺陷。那么我们递归地再对该结点判断其叔父颜色，递归地执行对应颜色的双红结点的处理。最坏的情况下也只是会递归的处理到根结点，因此整个双红缺陷蔓延的过程迟早会终止。

需要强调的一点是：尽管这一个调整过程，从B-树的角度来看，的确发生了拓扑结构的变化 。但是从红黑树的角度来看，除了相关结点的颜色发生了变化，红黑树的拓扑连接关系并没有发生变化。因此，红黑树的重染色操作的次数可能会高达 $O(logh)$，但是拓扑结构的变化依然控制在 $O(1)$ 的范围内。

5. 红黑树的删除

相对于插入，红黑树的删除情况更多，也更为复杂一些。因此，我们更需要通过提升变换，将红黑树映射为B-树，并站在B-树的角度，翻过来理解红黑树的过程及原理。

1. 首先按照二叉搜索树的常规删除算法，删除指定的关键字 $x$：$r=reomveAt(x)$
   【解释】：这里指的是待删除结点 $x$ 将由其孩子结点 $r$ 替代（替代者 $r$ 有可能就是一个实际不存在的外部结点），如下图（删除的结点 $x$ 不一定必须是红色，下图只是举例）
   
2. 删除之后，红黑树的拓扑结构依然保持完整，但是红黑树的性质未必能继续满足，需要进行调整（非常类似AVL）。

【解释】我们可以针对删除后红黑树的性质逐条分析：
（1）首先红黑树的根和外部结点为黑色，这个性质并没有收到影响；

（2）删除后在此局部有可能会出现两个红色结点相连的双红缺陷情况（假设之前 $x$ 为黑，$p、r$ 为红），当然这种情况可以通过之前在插入里学的解决办法处理。

（3）删除后在被删除结点 $x$ 所在的通路上黑结点的数目（黑深度）却有可能发生变化。

下面，我们重点讲解如何对黑深度进行调整。

5.1 调整：x 与 r 存在红结点

对于（3）中有一种情况比较好处理，也就是被删结点 $x$ 与其替代者 $r$ 两者中有一个是红色的，如下图

对于这一类情况，直接将替代者 $r$ 在替代完成后染为黑色即可，如下图。

为什么这么做可行呢？因为我们讲过，黑色指向红色的虚边，可以通过红结点提升来“合并”，对于红黑树的黑高度是没有影响的。因此删除后将 $r$ 置为黑色，可以等价在原树中删除了一条虚边，所以所有外部结点的黑高度将依然保持原状。

5.2 调整：双黑缺陷

然而，遗憾的是有可能被删除的结点 $x$ 以及他的替代者 $r$ 在删除前都是黑色结点，这种情况我们也称为双黑缺陷

如上图，如果真的删除了 $x$，用黑色的 $r$ 代替，则必然会丢失一个黑深度，全树的黑深度不再统一，破坏了红黑树的规则。我们不妨换一个角度，用B-树的视角看看，问题究竟出在哪？

因为 $x$ 和 $r$ 都是黑色的，那么对应的4阶B-树中 $x$ 将独立的成为一个结点，在唯一的这个关键字被删除之后，该结点也就自然发生了下溢。因此我们后面的调整算法与其说是修复“双黑缺陷”，不如说是修复B-树的下溢。

因此，只需借助B-树的下溢修复算法，即可得到对应的红黑树双黑修复算法。

5.2.1 双黑缺陷-1

我们知道，发生了下溢时，第一件事情就是下溢结点左顾右盼，看看兄弟结点能否借一个结点过来。

因此，对应双黑缺陷-1的情况就是：$x$ 相邻的左右兄弟结点 $s$ 为黑，且至少拥有一个红孩子 $t$（这里很好理解，有了红孩子就可以上提和 $s$ 合并，那么 $x$ 的左兄弟就相当于能借一个盈余结点出来，如果遗忘的话请回顾B-树的操作）

经过旋转之后，红黑树调整的结果如右图，现在将右图中的 $t,s,p$ 分别重命名为 $a,b,c$，$r$ 保持黑色，$a,c$ 染黑，$b$ 继承 $p$ 的颜色，因为 $s$ 继承了原来 $p$ 的颜色，因此新的局部结构也不会对红黑树的其他部分造成影响。

现在回过头来，我们发现这种情况还是比较简单的，因为 $s$ 作为兄弟结点起码还有一个红孩子，足够富有，能够提供旋转解决下溢的条件。那么可想而知，后面更困难的情况就是 $p$ 的左右孩子都是黑色，我们将继续讨论。

5.2.2 双黑缺陷-2R

双黑缺陷-2的情况就是：$x$ 相邻的左右兄弟结点 $s$ 为黑，且两个孩子均为黑。但是这里还需要根据 $s$ 和 $x$ 的父结点 $p$ 的颜色进行分类讨论，而双黑缺陷-2R就是双黑缺陷-2中，$p$ 为红色的情况。

老规矩，先将红色结点 $p$ 上提，转换为B-树，然后因为被删除的结点左子树不够借，无法进行旋转修复，因此通过让 $p$ 下来合并，注意这里 $s$ 和 $p$ 要交换颜色，最后恢复成变换后的红黑树。

那么这里有的小伙伴就会问了，因为原来B-树中 $p$ 结点所在的结点因为下层合并借走了一个关键字，是否会因此造成原结点下溢呢？事实上是不会的，因为既然 $p$ 是红色的，那么 $p$ 的父结点一定是黑色的，故即使 $p$ 被下面合并借走了以后也不会发生下溢。

这也是为什么我们要把 $p$ 的颜色单独拎出来分类的原因。

5.2.3 双黑缺陷-2B

而双黑缺陷-2R就是双黑缺陷-2中， $x$ 相邻的左右兄弟结点 $s$ 为黑，且两个孩子均为黑，$p$ 为黑色的情况。

整个流程和双黑缺陷-2R处理过程非常类似，只是当 $p$ 因为要解决下层下溢问题，被从原结点借出之后，原结点一定会下溢。故下层的下溢会引发上层的下溢。这种传播最多可以达到 $logh$ 次。但是，我们可以惊奇的发现，即使传播了 $logh$ 次，每一次从红黑树的角度仅仅变换了 $s$ 结点的颜色。

因此，双黑缺陷-2B的解决策略在拓扑结构的改变上依然是 $O(1)$ 的，是非常高效的。

那么，之前我们讨论的双黑缺陷问题时，都是讨论在 $s$ 为黑色结点的前提下的调整办法，那么当 $s$ 为红色将如何处理呢？

5.2.4 双黑缺陷-3

双黑缺陷-3是指： $x,r$ 为黑，$s$ 为红的情况。

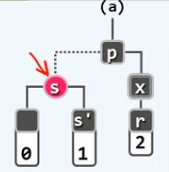
实际上，对于这种情况我们并不需要做什么实质性的处理，而只需要将其转化为此前我们所介绍的某两种子情况，为此，我们必须还要站在对应B-树的角度分析问题，如下图。

首先，依然是红色结点上提，转换为B-树视角。因为是同一个结点之内，我们不妨直接上 $s$ 和 $p$ 互换颜色，而堆B-树无需做任何的结构调整。当然，当恢复到对应的红黑树之后，却需要做一次拓扑结构的调整，因为原来 $s$ 的父亲指向 $p$，现在 $p$ 的父亲指向 $s$，也就是相当于在红黑树中，围绕着结点 $p$，做一次AVL树中的右旋操作，同时互换 $s$ 和 $p$ 的颜色。

即使经过了上述处理，你可能有些失望，因为现在仍然没有解决黑高度变化问题。但是，我们可以发现，现在待删除结点 $x$ 的兄弟 $s^{\prime }$ 已经变为了黑色，$x$ 的父结点已经变为了红色，于是我们就可以跳出双黑缺陷-3这种情况，而转入之前所讨论的情况。更具体一点，只会转入时间复杂度相对更小的双黑缺陷-1和双黑缺陷-2R这两种情况。

因此，我们可以断定，经过如此调整之后，红黑树的性质必然全局恢复。