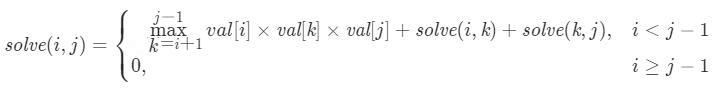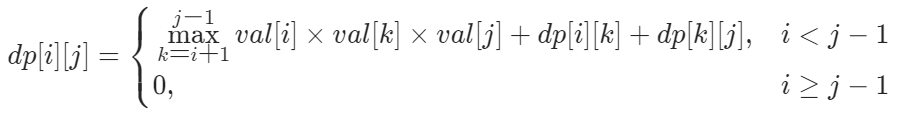题目描述
有 n 个气球,编号为0 到 n - 1,每个气球上都标有一个数字,这些数字存在数组?nums?中。
现在要求你戳破所有的气球。戳破第 i 个气球,你可以获得?nums[i - 1] * nums[i] * nums[i + 1] 枚硬币。?这里的 i - 1 和 i + 1 代表和?i?相邻的两个气球的序号。如果 i - 1或 i + 1 超出了数组的边界,那么就当它是一个数字为 1 的气球。
求所能获得硬币的最大数量。
测试样例
示例 1:
输入:nums = [3,1,5,8]
输出:167
解释:
nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = ?3*1*5 ? ?+ ? 3*5*8 ? + ?1*3*8 ?+ 1*8*1 = 167示例 2:
输入:nums = [1,5]
输出:10提示:
n == nums.length
1 <= n <= 500
0 <= nums[i] <= 100
题解
我们观察戳气球的操作,发现这会导致两个气球从不相邻变成相邻,使得后续操作难以处理。于是我们倒过来看这些操作,将全过程看作是每次添加一个气球。
方法一:记忆化搜索
定义方法solve,令solve(i,j) 表示将开区间 (i,j) 内的位置全部填满气球能够得到的最多硬币数。
- 当 i ≥ j ? 1 时,开区间中没有气球,solve(i,j)的值为0;
- 当 i < j ? 1 时,我们枚举开区间(i,j) 内的全部位置k,令mid为当前区间第一个添加的气球,该操作能得到的硬币数为val[j]val[i]×val[k]×val[j]。同时我们递归地计算分割出的两区间对solve(i,j) 的贡献,这三项之和的最大值,即为solve(i,j) 的值。这样问题就转化为求solve(i,k) 和solve(k,j) ,可以写出方程:
?为了防止重复计算,用rec数组存储solve?的结果,使用记忆化搜索的方法优化时间复杂度。
时间复杂度:
?
空间复杂度:
方法二:动态规划
按照方法一的思路,我们发现我们可以通过变换计算顺序,从「自顶向下」的记忆化搜索变为「自底向上」的动态规划。
令 dp[i][j] 表示填满开区间(i,j) 能得到的最多硬币数,那么边界条件是i ≥ j ? 1,此时有dp[i][j]=0。
可以写出状态转移方程:
?最终答案即为dp[0][n+1]。
【注】实现时要注意到动态规划的次序。i 从n-1到0; j从i+2 到 n+1; k 从i+1到j-1。这样设置顺序的目的是,计算时会用到更小的行列中的结果,所以从大到小计算 i 正好符合要求。
代码
方法一:记忆化搜索
class Solution {
// 方法一: 记忆化搜索
// 开辟一个新数组,方便处理头尾
public int[] val;
// 用来记忆已经计算过的结果
public int[][] rec;
public int maxCoins(int[] nums) {
int n = nums.length;
val = new int[n + 2];
for (int i = 1; i <= n; i++) {
val[i] = nums[i - 1];
}
val[0] = val[n + 1] = 1; // 首尾界外
rec = new int[n + 2][n + 2];
for (int i = 0; i < n + 2; i++) {
Arrays.fill(rec[i], -1); // 初始化为-1
}
return sovel(0, n + 1);
}
// 计算rec
public int sovel(int left, int right) {
if (left >= right - 1) { // i与j之间没有空位置
return 0;
}
if (rec[left][right] != -1) { // 已经计算过
return rec[left][right];
}
for (int i = left + 1; i < right; i++){
int sum = val[left] * val[i] * val[right];
sum += sovel(left, i) + sovel(i, right);
rec[left][right] = Math.max(rec[left][right], sum);
}
return rec[left][right];
}
}方法二:动态规划
class Solution {
// 方法二: 动态规划
public int maxCoins(int[] nums) {
int n = nums.length;
int[] val = new int[n + 2];
int[][] dp = new int[n + 2][n + 2];
val[0] = val[n + 1] = 1; // 首尾界外
for (int i = 1; i <= n; i++) {
val[i] = nums[i - 1];
}
for (int i = n - 1; i >= 0; i--) {
for (int j = i + 2; j <= n + 1; j++) {
for (int k = i + 1; k < j; k++) {
int sum = val[i] * val[k] * val[j];
sum += dp[i][k] + dp[k][j];
dp[i][j] = Math.max(dp[i][j], sum);
}
}
} // for
return dp[0][n + 1];
}
}