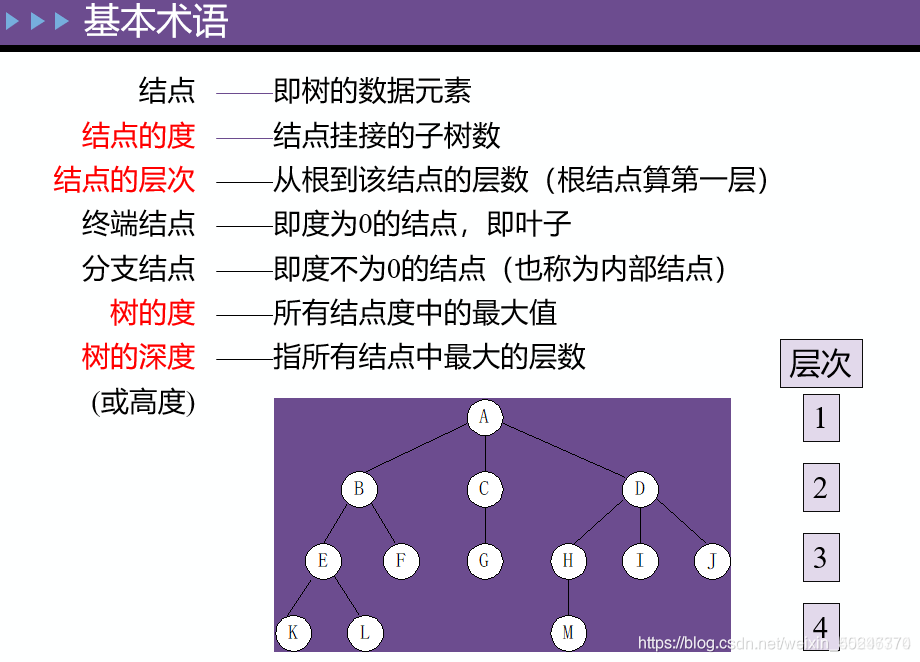
树和二叉树
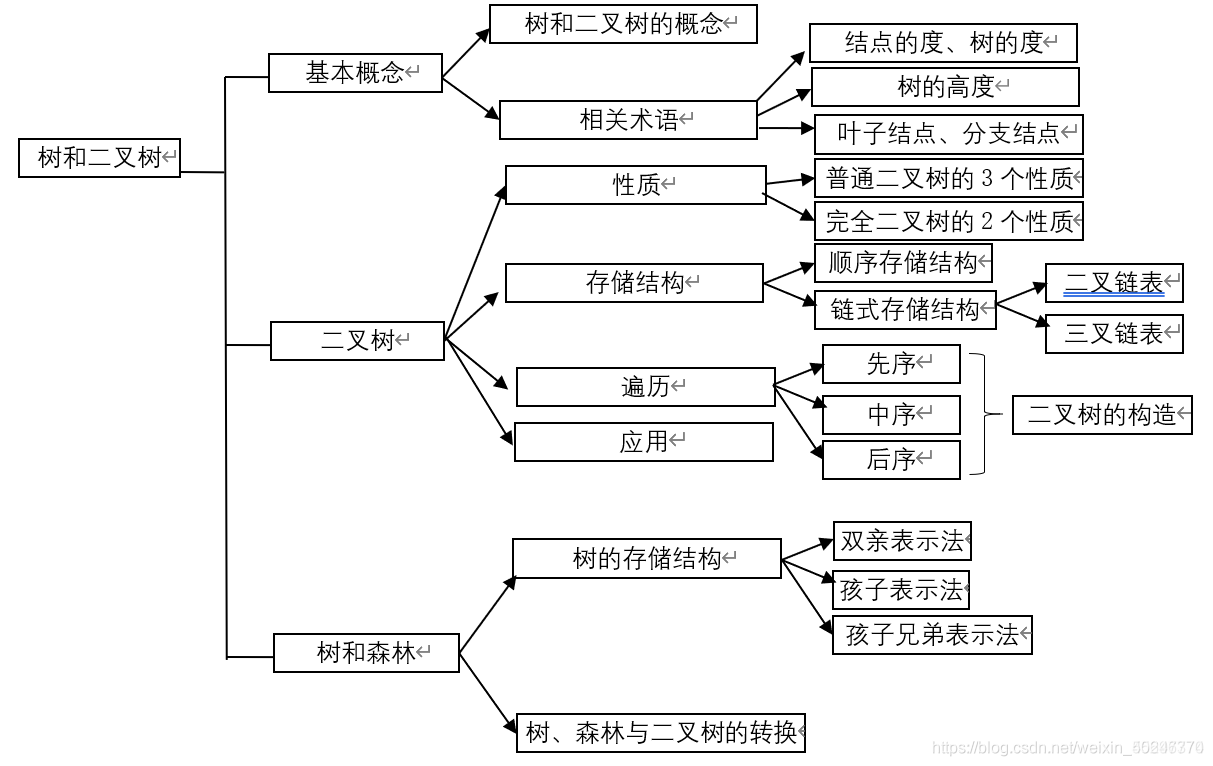
树:是N(N≥0)个结点的有限集合,N=0时,称为空树,这是一种特殊情况。
树的定义是递归的,是一种递归的数据结构。树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
- 树的根结点没有前驱结点,除根结点之外的所有结点有且仅有一个前驱结点。
- 树中所有结点可以有零个或者多个后继结点。
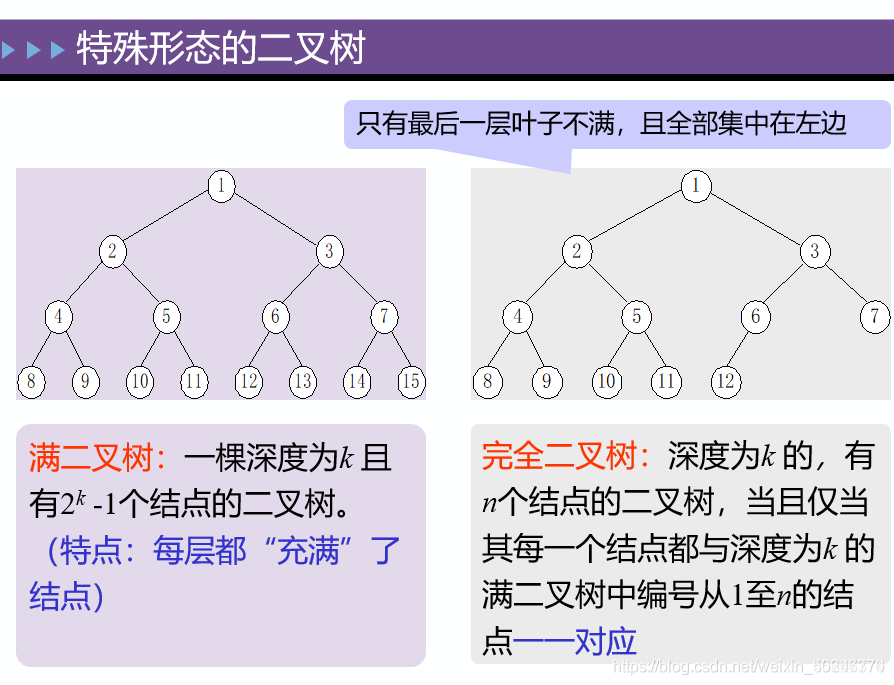
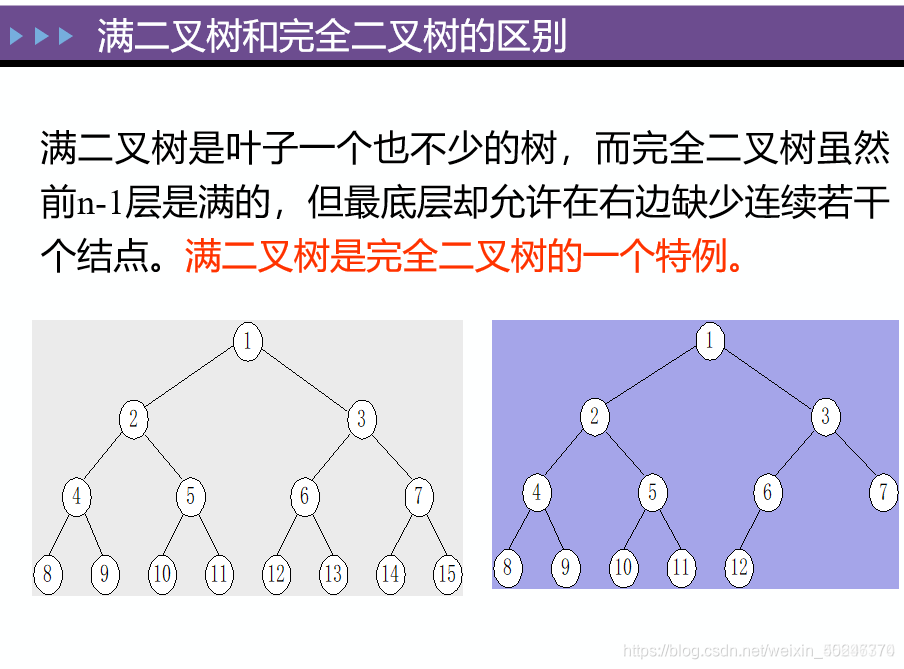
先(前)序遍历: 对访问到的每个结点,先访问根结点,然后是左结点,然后是右结点。
中序遍历: 对访问到的每个结点,先访问左结点,然后是根结点,然后是右结点。
后序遍历: 对访问到的每个结点,先访问左结点,然后是右结点,然后是根结点。
树转二叉树
1.兄弟+横线
树中的每一个结点,如果该结点有兄弟结点,那么就在这几个兄弟结点之间进行连线。
2.保存长子线
对于树中的每一个结点,如果其有多个子节点,保存其第一个子节点的连线,去除其他子节点的连线。
3.调整位置
对每个结点调整一定的位置,使其符合二叉树的标准。
森林转二叉树
1.将每课树转换成二叉树
2.将每课树的根结点连接起来,把每棵树的根当做兄弟结点处理,兄弟加横线
3.旋转调整位置
二叉树转化树
1.若某结点的左孩子结点存在,将左孩子结点的右孩子结点、右孩子结点的右孩子结点……都作为该结点的孩子结点,将该结点与这些右孩子结点用线连接起来;
2.删除原二叉树中所有结点与其右孩子结点的连线;
3.调整位置
二叉树转化森林
1.先把每个结点与右孩子结点的连线删除,得到分离的二叉树;
2.把分离后的每棵二叉树转换为树;
3.调整位置